ОСНОВЫ СТРОЕНИЯ И КИНЕТИКИ ФЕРМЕНТОВ В БИОЛОГИЧЕСКИХ СИСТЕМАХ - О. А. Науменко - 2017
2 Общие вопросы кинетики и термодинамики ферментативных реакций
2.1 Законы классической термодинамики в биохимии
В последние 30 лет наблюдается бурное развитие ферментативной кинетики. Ферментативная кинетика изучает изменение скорости ферментативных реакций в зависимости от концентрации фермента, концентрации субстрата, наличия активаторов, ингибиторов, изменения температуры и PH среды, а также механизмы регуляции активности фермента в ходе реакции.
2.1.1 Основные понятия кинетики и термодинамики. Термодинамические системы
Кинетика - это раздел физики, изучающий изменение параметров термодинамической системы в ходе различных термодинамических процессов.
Ферментативная кинетика изучает законы термодинамики: тепловой и энергетический обмены в биологических системах. При этом живые биологические системы, могут достигать динамического или стационарного состояния (динамического равновесия), в том случае, когда количество веществ и энергии, пришедшее в систему равно количеству вещества, ушедшего из системы.
Ферментативная кинетика изучает механизм, энергетику, регуляцию и изменение конформации ферментов в ходе ферментативных реакций. Изучением превращением энергии в биологических системах занимается раздел биохимии - биоэнергетика.
Химическая термодинамика использует законы термодинамики применительно к термодинамическим системам. Совокупность тел, участвующих в реакции называется термодинамической системой (ТС), а тела, не входящие в систему, называются внешним окружением. Термодинамические системы классифицируются на открытые и закрытые. Законы термодинамики применимы только к закрытым системам.
Закрытые системы обмениваются с окружающей средой только энергией, но не массой. Открытые системы, способны обмениваться с окружающей средой массой и энергией, а при определенных условиях достигать динамического равновесия или стационарного состояния, но не термодинамического равновесия с максимумом энтропии.
Биологические организмы - открытые термодинамические системы, которые обмениваются с окружающей средой энергией и веществом.
В термодинамически равновесных системах нельзя наблюдать макроскопических изменений. Их внутренняя энергия минимальна, и они находятся в состоянии полной беспорядочности. Живые системы достигают термодинамического равновесия только после смерти.
Все открытые системы вместе с их окружением образуют закрытую систему.
При наличии теплообмена и возможности хотя бы частичной диффузии между телами, составляющими систему, образуется термодинамическая система. Термодинамическая система может взаимодействовать со своим окружением, и это взаимодействие можно обнаружить по переносу тепла или совершению работы.
В том случае, когда взаимодействие системы со средой полностью отсутствует, система называется изолированной.
Если состояние термодинамической системы остается неизменным и причиной этого не является какой-либо внешний стационарный процесс, говорят, что система находится в равновесии. Если система состоит из одной фазы, то она гомогенная, в противном случае - гетерогенная.
Законы термодинамики применимы к закрытым системам. Поэтому для исследований и расчетов в биоэнергетике ввели понятие изолированной системы (минимальный обмен энергии).
Термодинамические системы можно классифицировать по совокупности их свойств. Свойства термодинамической системы - называются термодинамическими параметрами системы.
Экстенсивные свойства, такие как вес и объем, пропорциональны массе. Интенсивные свойства, такие как температура, давление, не зависят от массы. Состояние системы, находящейся в равновесии, можно описать совокупностью ее интенсивных свойств. Термодинамические параметры системы описывают только данное состояние, не учитывая предшествующих. Следовательно, изменение параметров при переходе системы из одного состояния в другое не зависит от пути реакции, а определяется только термодинамическими параметрами начального и конечного состояний.
Масса (М) и объем (V) - это общепринятые термины. Давление (Р) - характеризует взаимодействие с внешним окружением, измеряемое как сила, приходящаяся на единицу площади поверхности.
Температура (Т), которая определяется интенсивностью теплового движения молекул, образующих систему, не простое понятие, оно включает в себя понятие разности теплоты. Между телами различной температуры происходит теплоперенос, приводящий к выравниванию температур. Абсолютная шкала температур основана на втором законе термодинамики. Ее начало находится на абсолютном нуле (- 273,16о К).
При абсолютном нуле часть энергии любого вещества, которая зависит от температуры (тепловая энергия), равна нулю, хотя энергия частиц, составляющих вещество, при нулевой температуре, естественно, не исчезает.
2.1.2 Термодинамический процесс
Любое изменение параметров термодинамической системы, приводящее к изменению хотя бы одного термодинамического параметра, называется термодинамическим процессом (ТП).
Признаки равновесного термодинамического процесса. Если в ходе термодинамического процесса система проходит равновесные состояния, то при данных условиях работа, совершаемая самой системой, будет максимальна, а работа, свершаемая над системой, - минимальна, в таком случае говорят о равновесном ТП.
И наоборот, ТП, протекающий при некотором ограниченном воздействии на систему, определяется как неравновесный ТП. Работа, совершенная такой системой, меньше, чем максимальная работа в равновесном процессе.
Если единственным результатом обратного процесса в изолированной системе является возвращение системы из конечного состояния в исходное, то такой процесс называют обратимым ТП.
Если в результате прямой или обратной реакции в системе или в ее окружении имеют место длительные изменения термодинамических параметров системы, то ТП называют необратимым.
Причина необратимости в том, что процессы в ТС протекают через неравновесные состояния. Термодинамические параметры однозначны только для обратимых процессов, когда система находится в равновесии в любой момент времени и в каждой ее части. Если вывести систему из состояния устойчивого равновесия, то возникнет термодинамический процесс, препятствующий внешнему воздействию (принцип Ле Шателье - Брауна).
2.1.3 Первый закон термодинамики
Первый закон термодинамики гласит о том, что энергия в ТС не может быть получена из ничего и не может быть уничтожена, а может только превращаться из одного вида в другой. Это означает, что содержание энергии (U) в термодинамической системе увеличивается при совершении ТС работы (А) или передачи тепла (Q):
∆U = А + Q
где ∆U - изменение энергии ТС; А - работа ТС; Q - теплота ТС.
В случае ТП, когда изменение энергии системы ∆U = 0,
А = - Q (2.2)
Отсюда проистекает невозможность создания вечного двигателя первого рода.
Если над ТС не совершается никакой работы, т. е. ∆U = ∆Q, то при равновесном давлении (∆Р = 0) для объема V можно определить новую функцию:
H = U + PV (3.3)
где Н - энтальпия (или теплосодержание ТС); U - внутренняя энергия ТС; Р - давление в ТС; V - объем ТС.
Закон Гесса: теплота превращения в ТС не зависит от пути протекания ТП.
При экзотермическом процессе - выделенная ТС теплота считается отрицательной величиной (теплосодержание системы уменьшается), т. к. положительным условно считается тепло, полученное ТС (+Н)- это эндотермический процесс, сопровождающийся увеличением теплосодержания ТС. Протекающие в живых организмах анаболические процессы представляют собой эндотермические реакции, а катаболические - экзотермические.
2.1.4 Второй закон термодинамики
Все процессы в природе протекают в одном направлении, т. е. они необратимы. Необратимость в термодинамике означает, что ТП процесс не может идти в ТС в обратном направлении без изменения энтропии. Энтропия выражается следующим уравнением:
∆S = ∆Q / Т, (3.4)
где ∆S - изменение энтальпии ТС; ∆Q - изменение теплоты ТС; Т - температура ТС.
Дифференциальное изменение энтропии равняется отношению элементарного количества теплоты к абсолютной температуре. Основываясь на втором законе термодинамике, все природные процессы, не противоречащие первому закону термодинамики, можно разделить на две группы:
- самопроизвольные ТП при данных условиях;
- не самопроизвольные ТП.
Невозможна реакция, дающая только перенос тепла от тела с более низкой температурой к телу с более высокой температурой. Это означает, что работа в ТС не может быть выполнена исключительно за счет тепловой энергии окружающей среды, другими словами, невозможно создание вечного двигателя второго рода.
При обратимых ТП в изолированной ТС энтропия остается неизменной, при необратимых процессах она возрастает. Если в результате необратимого процесса изолированная система приходит в равновесие, то ее энтропия достигает максимума. Следовательно, изменение энтропии определяет направление ТП и одновременно условия термодинамического равновесия.
Принцип постоянства или увеличения энтропии справедлив только для изолированной системы. В изолированной системе увеличение энтропии служит мерой необратимости процесса. Живые организмы сохраняют внутреннюю упорядоченность (постоянную энтропию), получая дополнительную энергию в виде пищевых веществ (химическая энергия) или солнечного света (электромагнитная энергия) из окружающей среды и возвращают в нее такое же количество энергии в другой форме, главным образом в форме тепла, которое рассеивается во всей
остальной Вселенной. Живые организмы непрерывно должны повышать свою энтропию для поддержания внутреннего порядка.
2.1.5 Характеристические функции состояния ТС
Характеристической функцией называется такая функция ТС, посредством которой могут быть выражены ее свойства. Под потенциалом понимают функцию, изменение которой связано с работой ТС. В термодинамике наиболее широко используют следующие характеристические функции:
1) изохорно-изотермический потенциал ТС - энергия Гельмгольца (∆F);
2) изобарно-изотермический потенциал ТС - энергия Гиббса (∆G);
3) внутренняя энергия ТС (∆U);
4) энтальпия ТС (∆Н);
5) энтропия ТС (∆S).
Внутренняя энергия (∆U) ТС определяется согласно уравнения:
∆U = T∆S - Р∆V (2.5)
где ∆U -изменение внутренней энергии ТС; Т - температура; ∆S - энтропия; Р - давление; ∆V - объем.
Энтальпия ∆Н - это изменение теплосодержания системы при постоянном давлении и энтропии.
∆Н = T∆S + V∆P, (2.6)
где ∆Н - изменение теплосодержания ли энтальпии ТС; Т - температура; ∆S - энтропия; ∆Р - давление; V - объем.
Энтропия ∆S - это мера неупорядоченности ТС, величина, равная количеству теплоты, поступающей в ТС при постоянной температуре.
∆S = ∆Q / Т, (2.7)
где ∆S -изменение энтропии ТС; Т - температура; ∆S - энтропия; ∆Q - изменение теплоты.
Энергия Гельмгольца - это свободная энергия ТС, идущая на совершение полезной работы при постоянном объеме и температуре (изохорно-изотермический потенциал).
F = U - TS, (2.8)
где F - свободная энергия ТС; Т - температура; ∆S - энтропия; U - внутренняя энергия ТС.
Энергия Гиббса - это свободная энергия ТС, идущая на совершение системой полезной работы при постоянном давлении и температуре (изобарно- изотермический потенциал).
G = H — TS (2.9)
где G - энергия Гиббса; Т - температура; S - энтропия; Н - энтальпия.
Контрольные вопросы по изучаемой теме
1. Что изучает ферментативная кинетика?
2. Что такое термодинамический процесс и какие его виды?
3. Дайте понятие термодинамической системы?
4. Какие бывают термодинамические системы?
5. Что значит открытая термодинамическая система?
6. Сформулируйте первый закон термодинамики.
7. Сформулируйте второй закон термодинамики.
8. Термодинамический процесс и его виды.
9. Энтальпия и энтропия.
10. Характеристические функции в термодинамике.
2.2 Кинетика Михаэлиса - Ментена
2.2.1 Химическая кинетика. Понятие порядка реакции
Химическая кинетика - учение о химическом процессе, его механизме и закономерностях развитии во времени.
Химическая кинетика изучает скорость химической реакции с учетом различных условий: концентрации реагирующих веществ, температуры, pH среды, наличия или отсутствия катализаторов.
В химии одной молекуле вещества соответствует один моль вещества, а количество молей вещества обозначается коэффициентом реакции. В соответствии с законом действующих масс, порядок реакции определяется суммой степеней концентраций реагирующих веществ.
Например, в ходе химической реакции 1 моль вещества А превращается в 1 моль вещества В: 1 моль А —> 1 моль В
Это мономолекулярная реакция, или реакция первого порядка.
Если в ходе реакции, 1 моль вещества А взаимодействует с 1 молем вещества В и в результате их взаимодействия образуется 1 моль вещества С: А + В —> С, то эта реакция будет называться бимолекулярной или реакцией 2 порядка.
2.2.2 Кинетика Михаэлиса - Ментена
В 1835 году Ян Берцелиус впервые предположил, что реакции живого организма осуществляются благодаря «новой силе», которую он назвал «каталитической». Берцелиус сформулировал принцип катализа, включив в число каталитических агентов и фермент диастазу, которая катализировала гидролиз крахмал быстрее, чем серная кислота.
Предварительные эксперименты по изучению кинетики ферментативных реакций показали, что скорость ХФР, описываемой уравнением: Е + S —> Е + Р, не зависит от концентрации фермента и субстрата так, как в случае обычной химической реакции второго порядка.
Самая ранняя попытка математически описать ферментативные реакции была предпринята Дюкло в 1898 году. Браун (1902) и независимо от него Анри (1903) впервые выдвинули гипотезу об образовании в ходе реакции фермент - субстратного комплекса.
В 1913 году Михаэлис и Ментен опубликовали свою теорию общего механизма ферментативных реакций. Их уравнение стало фундаментальным принципом всех кинетических исследований ферментов.
Так, Михаэлис и Ментен предположили, что механизм обычной двухстадийной ХФР описывается схемой:
![]() (2.10),
(2.10),
где: Е - фермент; S - субстрат; ES - фермент - субстратный комплекс; Р - продукт ХФР; k1 - константа диссоциации первой стадии (реакция второго порядка);
к2 - константа диссоциации второй стадии распада фермент субстратного комплекса (реакция первого порядка).
В данной схеме k1 = кs, где кs - константа диссоциации фермент субстратного комплекса, а скорость ХФР определяется скоростью распада фермент - субстратного комплекса до продукта, т. е. скоростью второй стадии:
v0 = k2 [ES], (2.11)
где: k2 - константа диссоциации второй стадии распада фермент субстратного комплекса (реакции первого порядка); v0 — начальная скорость ХФР; [ES] - концентрация фермент - субстратного комплекса.
Модель предполагает, что равновесие первой стадии ХФР между свободными ферментом, субстратом и фермент - субстратным комплексом устанавливается быстро по сравнению со скоростью всей ХФР (быстро устанавливающееся равновесие первой стадии к2 «к1, k-1). В этом случае вторая стадия реакции практически не влияет скорость первой стадии, и поэтому для выражения концентрации фермента можно воспользоваться константой диссоциации фермент - субстратного комплекса Ks.
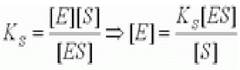 (2.12)
(2.12)
где Ks - константа диссоциации фермент субстратного комплекса; [Е] - концентрация фермента; [S] - концентрация субстрата; [ES] - концентрация фермент - субстратного комплекса.
Общая концентрация фермента в реакционной смеси выражается уравнением материального баланса по ферменту:
[E]0=[E] + [ES] = [ES] (Ks/[S]+1), (2.13)
где [Е]0 - начальная концентрация фермента; Ks - константа диссоциации фермент субстратного комплекса; [Е] - концентрация фермента; [S] - концентрация субстрата;
[ES] - концентрация фермент - субстратного комплекса.
Тогда концентрация фермент - субстратного комплекса равна:
![]() (2.14)
(2.14)
Реакция достигает максимальной скорости, когда весь фермент находится в комплексе с субстратом:
Vmax=ks[ES]=ks[E]0, (2.15)
где Vmax - максимальная скорость ХФР; ks - константа диссоциации фермент - субстратного комплекса; [Е]0 - начальная концентрация фермента; [S] - концентрация субстрата; [ES] - концентрация фермент - субстратного комплекса.
Это условие выполняется, если реакция протекает при избыточной концентрации субстрата: [S]0>> [Е]0. Из предыдущих уравнений получим:
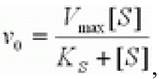 (2.16)
(2.16)
где v0 - начальная скорость ХФР; Vmax - максимальная скорость ХФР; Ks - константа диссоциации фермент - субстратного комплекса; [S] - концентрация субстрата.
Это и есть классическое уравнение Михаэлиса - Менте на, которым и сегодня пользуются для описания кинетики ХФР, а величина константы Михаэлиса при данных условиях Км = Ks и представляет собой меру сродства фермента субстрату. Максимальная скорость ХФР достигается тогда, года концентрация фермент - субстратного комплекса численно равна общей концентрации фермента (т. е. когда весь фермент связан с субстратом в комплекс).
В этом случае зависимость скорости ХФР от концентрации (Е) во многом зависит от соотношений концентрации фермента и субстрата. Если концентрация субстрата достигает максимальной и значительно превышает концентрацию фермента ([S]»[E]), то тогда скорость ХФР возрастает линейно прямо пропорционально концентрации фермента, т.е. чем выше концентрация [Е], тем выше будет скорость реакции.
2.2.3 Ограничения кинетики Михаэлиса-Ментена
Михаэлис и Ментен вывели уравнение с учетом двух условий: быстро устанавливающееся равновесие первой стадии и значительный избыток субстрата. Позднее было доказано, что уравнение справедливо, при выполнении семи условий или постулатов.
Постулаты выполнения уравнения Михаэлиса - Ментена:
1) в ходе реакции образуется кинетически устойчивый фермент-субстратный комплекс, который существует в определенной концентрации в течении определенного времени;
2) определяемая с помощью уравнения константа Ks является константой диссоциации фермент-субстратного комплекса: это справедливо, только если к2« к1, к-1;
3) концентрация субстрата не меняется в ходе реакции, то есть [S] = [S]0;
4) продукт реакции быстро отщепляется от фермента, то есть реакция двухстадийная;
5) вторая стадия реакции необратима. Так как это практически не выполнимо, мы принимаем во внимание только начальные скорости ХФР;
6) с каждым активным центром фермента связывается только одна молекула субстрата;
7) для всех реагирующих веществ вместо активностей можно использовать их концентрации.
2.2.4 Образование кинетически устойчивого фермент-субстратного комплекса (обоснование первого постулата)
К настоящему времени по данным рентгено - структурного анализа имеются сотни экспериментальных доказательств, демонстрирующих образование кинетически устойчивых фермент - субстратных комплексов в ходе ферментативных реакций. Хотя выдвигались также и другие теории, без образование в ХФР фермент - субстратного комплекса.
1. Теория телекинетических взаимодействий предполагает, что фермент увеличивает энергию молекулы субстрата с помощью каких-либо телекинетических взаимодействий (электростатическое притяжение или отталкивание, электромагнитное излучение и т. д.).
2. Теория упругих столкновений. Считается, что фермент передает энергию субстрату при упругих столкновениях. При этом молекула субстрата достигает энергии выше определенного уровня и может вступать в реакцию или разрушаться с образованием продуктов.
Несмотря на то, что для данных теорий были составлены кинетические уравнения, когда фермент отделен от субстрата растворителем (т. е. может происходить телекинез в передаче энергии субстрату), такие теории до сих пор не нашли экспериментального подтверждения.
Это означает, что образование кинетически устойчивого фермент- субстратного комплекса обязательно происходит во всех известных ферментативных реакциях. Поэтому первое условие, определяющее справедливость кинетики Михаэлиса - Ментена, можно считать доказанным.
2.3 Природа константы К в уравнении Михаэлиса - Ментена
2.3.1 Стационарная кинетика Бриггса и Холдейна (обоснование второго постулата)
Второй постулат формулирует, что константа Ks в уравнении (2.16) является константой диссоциации фермент-субстратного комплекса.
Бриггс и Холдейн в 1925 году доказали, что исходное уравнение Михаэлиса - Ментена справедливо только при условии к2 «к1, к-1 т. е. когда равновесие первой стадии (Е + S ⇄ES) устанавливается очень быстро по сравнению со скоростью установления равновесия второй стадии.
Поэтому такие кинетические механизмы, подчиняющиеся начальному условию Михаэлиса-Ментен и имеющие одну медленную стадию, относительно которой равновесия во всех других стадиях устанавливаются быстро, называются "быстрым равновесием".
Если к2 по порядку величины сравнима с к-1, то тогда используется кинетика Бриггса и Холдейна или кинетика стационарности: когда количество
образовавшегося фермент - субстратного комплекса равно количеству распавшегося. В этом случае уравнение начальной скорости ХФР будет следующим:
![]() (2.17)
(2.17)
Где V - скорость ХФР; Vmax - максимальная скорость ХФР; Км - константа Михаэлиса; [S] - концентрация субстрата; [Е] - концентрация фермента; К1 - константа диссоциации первой стадии (реакция второго порядка);
Данное уравнение аналогично уравнению (2.16), но оно расширяет область применимости исходного уравнения Михаэлиса-Ментена.
2.3.2 Природа константы К в уравнении Михаэлиса-Ментена
Если в ХФР выполняется условие быстро устанавливающегося равновесия первой стадии и k2«k1, к-1, то константа диссоциации К, которая будет найдена при исследовании зависимости скорости ХФР от концентрации субстрата, является константой диссоциации фермент - субстратного комплекса (первой стадии) Ks.
При выполнении условия стационарности: к2 = к1 (кинетика Бриггса и Холдейна), найденная тем же способом константа будет являться константой Михаэлиса, где Км= (к-1 + к2)/ к1.
В других реакциях, когда k1 «k2 константа Михаэлиса равняется k2/k1 и называется, согласно Ван Слайку, кинетической константой Кs.
При изменении условий реакции значение константы К также может изменяться. Так, например, в случае пероксидазы, при высокой концентрации субстрата - донора протонов, эта константа является кинетической константой (Кк). При уменьшении концентрации субстрата - донора протонов, константа превращается в константу Михаэлиса - Км, а при очень низких уровнях субстрата - донора протонов получаем константу диссоциации фермент - субстратного комплекса - Ks.
Поскольку значение константы Михаэлиса меняется в зависимости от условий реакции, константу Км также обозначают, как Км (каж.). График зависимости скорости ферментативной реакции от начальной концентрации субстрата S согласно уравнения (2.16) будет иметь гиперболическую форму (рисунок 2.1). На данном графике видно, что в начале реакции скорость реакции возрастает прямо пропорционально линейно с увеличением концентрации субстрата. Порядок реакции в этом случае будет первым. Скорость реакции на данном отрезке достигает максимальной (Vmax), когда весь субстрат будет связан с ферментом, и константа ХФР будет соответствовать Ks.
Рисунок 2.1 - График зависимости скорости ферментативной реакции от концентрации субстрата S.
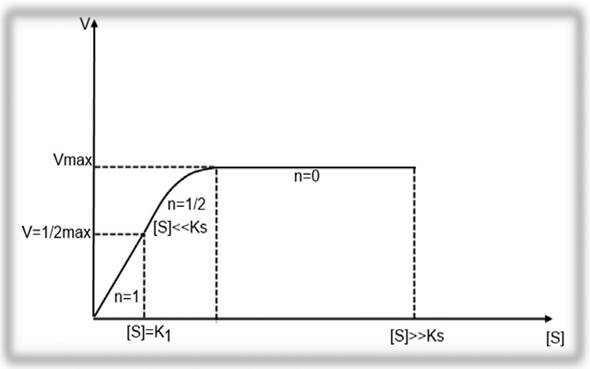
Далее при нарастании концентрации субстрата, график меняется с прямой на параболу. В этом случае порядок реакции становится дробным (п=1/2). В этой части реакции Sрасходуется, концентрация его уменьшается и становится [S] = Км, а скорость реакции равняется 1/2 от Vmax. При дальнейшем увеличении концентрации субстрата S, скорость реакции не увеличивается, а порядок реакции становится нулевым (n = 0), а скорость реакции V= const.
Таким образом, физический смысл константы Михаэлиса (Км) состоит в том, что это такая концентрация субстрата [S] при которой, скорость ХФР составляет 1/2 от максимальной.
Значение констант для каждой ферментативной реакции определяется экспериментально и их значение зависит от pH - среды, температуры, присутствия ингибитора (активатора). Если для фермента определена Vmах и Км, то можно рассчитать оптимальную концентрацию субстрата S.
2.3.3 Методы графического определения кинетических параметров
Для решения практических задач энзимологии график гиперболический зависимости скорости ферментативной реакции от концентрации субстрата S является весьма неудобным. Поэтому на практике используются методы линеаризации экспериментальных данных.
Наиболее часто для определения кинетических параметров ХФР используются координаты Лайнуивера - Берка (1/V и 1/S) и координаты Диксона - Ида (1/V и [S]).
Метод Лайнуивера - Берка называется методом двойных обратных величин. График зависимости скорости ХФР от концентрации субстрата имеет линейный вид и представлен на рисунке 2.2.
Рисунок 2.2 - График зависимости скорости ферментативной реакции от концентрации субстрата S по методу Лайнуивера - Берка.
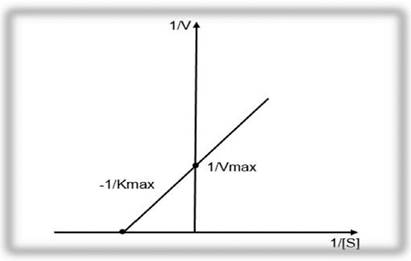
Определение обратных значений (1/V) скорости ХФР в координатах Лайнуивера - Берка ведется по формуле 2.18:
![]() (2.18)
(2.18)
где V - скорость ХФР; Vmах - максимальная скорость ХФР; Км - константа Михаэлиса; [S] - концентрация субстрата.
Контрольные вопросы по изучаемой теме
1. Порядок реакции и методы его определения.
2. История развития ферментативной кинетики.
3. Уравнение Михаэлиса-Ментена.
4. Ограничение кинетики Михаэлиса-Ментена.
5. Образование кинетически устойчивого фермент-субстратного комплекса.
6. Природа константы К в уравнения Михаэлиса-Ментена.
7. В чем физический смысл константы Михаэлиса.
8. Какой формы график зависимости скорости ХФР от концентрации субстрата согласно уравнения Михаэлиса-Ментена?
9. Какие координаты в зависимости Лайнуивера - Берка?
10. Что такое кинетическая константа?
11. Какие имеются доказательства первого постулата?
2.4 Кинетический анализ двухстадийных ферментативных реакций, не подчиняющихся уравнению Михаэлиса-Ментена
Третий постулат ферментативной кинетики гласит: концентрация субстрата не меняется в ходе реакции, то есть [S]t = [S]0. Это означает наличие достаточно большого избытка субстрата. Однако во многих случаях это условие не выполняется. С одной стороны, большой избыток субстрата не используется в реакциях «in vitro» с некоторыми ферментами из-за частого ингибирования субстратом ферментативной активности самого фермента. Обычно не достигается избыток субстрата и «in vivo».
В ферментативных реакциях, где субстрат не находится в избытке и, следовательно, его концентрация меняется с течением времени в ходе реакции, константа диссоциации примет вид:
![]() (2.19)
(2.19)
где Ks - константа диссоциации фермент - субстратного комплекса; [S]0 - начальная концентрация субстрата; [ES] - концентрация фермент - субстратного комплекса;
[Е]0 - концентрация фермента в начале реакции; [Р] - концентрация продукта ХФР.
Начальная скорость реакции тогда будет:
![]() (2.20)
(2.20)
где Vmax - максимальная скорость ХФР; Ks - константа диссоциации фермент - субстратного комплекса; [S]t -концентрация субстрата на данный момент времени.
2.4.1 Изменение концентрации субстрата в ходе ферментативной реакции (обоснование третьего постулата)
Уравнение (2.20) можно решить, используя два разных варианта условий ХФР, когда [S]0 ≠ [S]t:
1) если это неравенство выполняется из-за больших значений t, т. е. когда более 5% от начальной концентрации субстрата израсходовано за время реакции (в начале реакции условие избытка субстрата выполнялось);
2) если концентрацией фермента нельзя пренебречь по сравнению с концентрацией субстрата и, таким образом, нужно принимать во внимание концентрацию фермент - субстратного комплекса (время реакции мало, но условие избытка субстрата не выполнено изначально).
2.4.1.1 Решение первого варианта: Если t велико, a [ES] «[S]0, уравнение (2.20) переходит в следующее:
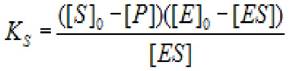 (2.21)
(2.21)
где Ks - константа диссоциации фермент - субстратного комплекса; [S]0- начальная концентрация субстрата; [ES] - концентрация фермент - субстратного комплекса;
[Е]0 - концентрация фермента в начале реакции; [Р] - концентрация продукта ХФР.
Для значения концентрации субстрата [S]t, которая меняется в ходе реакции, удовлетворительным приближением служит значение ([S]0+[S]t)/2. Тогда среднюю скорость можно выразить как:
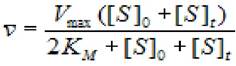 (2.22)
(2.22)
где Vmax - максимальная скорость ХФР; Км - константа Михаэлиса; [S]0- начальная концентрация субстрата; [S]t -концентрация субстрата на данный момент времени.
2.4.1.2 Решение второго варианта. Когда условие избытка субстрата не выполнено изначально, но расход субстрата не превышает 5%. В этом случае можно пренебречь концентрацией продукта [Р], но нельзя не учитывать концентрацию фермент-субстратного комплекса [ES],
![]() (2.23)
(2.23)
где Ks - константа диссоциации фермент - субстратного комплекса; [ES] - концентрация фермент - субстратного комплекса; [Е] - концентрация фермента;
Квадратное уравнение относительно концентрации субстрата:
![]() (2.24)
(2.24)
где Ks - константа диссоциации фермент - субстратного комплекса; [S]0 - концентрация субстрата в начале реакции; [S] - концентрация субстрата;
а - коэффициент, который равен:
а = Ks+[E]0 - [S]0, (2.25)
где Ks - константа диссоциации фермент - субстратного комплекса; [S]0 - концентрация субстрата в начале реакции; [S] - концентрация субстрата.
Решением данного квадратного уравнения является
 (2.26)
(2.26)
где Ks - константа диссоциации фермент - субстратного комплекса; [S]0 - концентрация субстрата в начале реакции; [S] - концентрация субстрата; а - коэффициент.
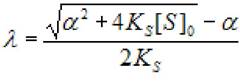 (2.27)
(2.27)
Тогда скорость реакции V можно выразить уравнением
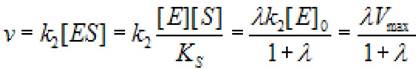 (2.28)
(2.28)
где к2 - константа диссоциации второй стадии; [S]0- начальная концентрация субстрата; [ES] - концентрация фермент - субстратного комплекса; [Е]0 - концентрация фермента в начале реакции; Vmax - максимальная скорость ХФР.
Выражая из последнего уравнения λ, получим
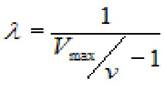 (2.29)
(2.29)
где V - скорость ХФР; Vmax - максимальная скорость ХФР.
При сравнении значений, рассчитанных данным методом, со значениями, полученными из точного, проинтегрированного уравнения Михаэлиса - Ментена, оказывается, что ошибка в определении Км составляет только 1% и 4% при расходовании 30% и 50% субстрата соответственно. Следовательно, данными уравнениями можно пользоваться для расчета кинетических параметром ХФР при больших промежутках времени реакции и расходовании субстрата.
2.4.2 Методика нахождения кинетических констант при условии [S]0 ≠ [S]t
Методика нахождения констант в данном случае выглядит следующим образом.
1. В предварительных экспериментах (при избытке субстрата) определяют Vmах;
2. В условиях [E]0~[S]0 определяют скорости реакции при разных концентрациях субстрата;
3. По уравнению (2.29) рассчитываем параметр λ для каждой вычисленной скорости;
4. По вычисленным параметрам λ определяем Ks.
По точке пересечения данной прямой с осью абсцисс находим Ks, тангенс угла наклона равен 1/[Е]0. Таким образом, изучение зависимости скорости ферментативной реакции от концентрации субстрата в условиях [E]0~[S]0позволяет определить абсолютную концентрацию активных центров фермента.
Контрольные вопросы по изучаемой теме
1. Что гласит третий постулат ферментативной кинетики?
2. Приближенное решение уравнения Михаэлиса-Ментен в случае больших времен протекания реакции.
3. Какие условия для первого варианта приближенного решения уравнения Михаэлиса-Ментен?
4. Какие условия для второго варианта приближенного решения уравнения Михаэлиса-Ментен?
5. Какова методика нахождения кинетических констант при условии [S]0 ≠ [S]t?
2.5 Влияние обратимых эффекторов на кинетику ферментативной реакции
2.5.1 Механизмы влияния обратимых эффекторов на кинетику ферментативной реакции
Вещества, изменяющие каталитическую активность фермента, называются эффекторами.
Взаимодействие фермента с эффектором представляет собой химическую реакцию и поэтому может быть полностью обратимым, частично обратимым или практически необратимым. Если процесс ингибирования необратим, то кинетическая реакция не подчиняется механизму Михаэлиса - Ментен, основой которого является наличие равновесия между свободной и связанной формами фермента.
В случае обратимых ингибиторов для описания кинетики ферментативной реакции можно воспользоваться уравнением Михаэлиса-Ментена. По влиянию ингибиторов на параметры ХФР их классифицируют:
а) конкурентные - ингибиторы, в присутствии которых повышается Км, a Vmax не меняется. Вызываемый такими ингибиторами эффект можно частично или полностью снять путем повышения концентрации субстрата. Примером может служить обратимое конкурентное ингибирование фермента сукцинилдегидрогеназы малоновой кислотой, субстратом которой является янтарная кислота (рисунок 2.3);
Рисунок 2.3 - Обратимое конкурентное ингибирование фермента сукцинилдегидрогеназы малоновой кислотой

б) неконкурентные - ингибиторы, инактивирующие фермент или фермент - субстратный комплекс путем уменьшения Vmax, но не влияющие на Км. В этом случае повышение концентрации субстрата не приводит к повышению скорости реакции. К неконкурентным ингибиторам относятся ионы тяжелых металлов, обратимо реагирующие с -SHгруппами цистеинов.
Многие из конкурентных ингибиторов по своей химической природе близки субстратам. Такие ингибиторы называются субстратными аналогами.
Неконкурентные ингибиторы связываются с аллостерическим центром фермента.
2.5.2 Кинетика ферментативных реакций, протекающих с участием эффектора
В общем случае влияние обратимого эффектора на двухстадийную ферментативную реакцию может быть передано схемой:
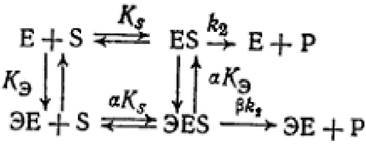 (2.30)
(2.30)
где Е - фермент; S - субстрат; Р - продукт реакции; ks - константа диссоциации фермент - субстратного комплекса; к2 - константа диссоциации второй стадии;
кэ - константа диссоциации комплекса фермент - эффектор; ЭЕ - комплекс фермент - эффектор; ЭES - тройной комплекс эффектор - фермент - субстрат.
Для начальной скорости ферментативной реакции (при условии [S]0, [Э]0>> [Е]0, где [Э] - концентрация эффектора, а - коэффициент, показывающий во сколько разменяется скорость первой стадии в присутствии эффектора, а β - коэффициент, изменения скорости второй стадии при установившихся равновесиях первой и второй стадиях ХФР, справедливо:
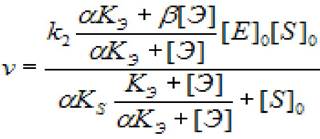 (2.31)
(2.31)
где [S]0 - начальная концентрация субстрата; [ES] - концентрация фермент - субстратного комплекса; [Е]0 - концентрация фермента в начале реакции; [Э] - концентрация эффектора; Ks - константа диссоциации фермент - субстратного комплекса; к2 - константа диссоциации второй стадии; кэ - константа диссоциации комплекса фермент - эффектор; а - коэффициент изменения скорости первой стадии; β - коэффициент, изменения скорости второй стадии.
В зависимости от численных значений α и β эффектор может выступать в роли либо ингибитора, либо активатора ферментативной реакции. Выделяют следующие виды ингибирования:
- полное конкурентное ингибирование;
- полное неконкурентное ингибирование;
- бесконкурентное ингибирование;
- простая активация;
- смешанное ингибирование;
- смешанное активирование.
2.5.2.1 Полное конкурентное ингибирование (α —> ∞, β не имеет определенного смысла), скорость ХФР определяется уравнением:
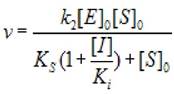 (2.32)
(2.32)
где [S]0 - начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; [I] - концентрация ингибитора; кs - константа диссоциации фермент - субстратного комплекса; к2 - константа диссоциации второй стадии; ki - константа диссоциации комплекса фермент - ингибитор.
Зависимость в координатах Лайнуивера - Берка имеет вид пучка прямых, пересекающихся на оси ординат (рисунок 2.4).
Рисунок 2.4 - График зависимости при полном конкурентном ингибировании
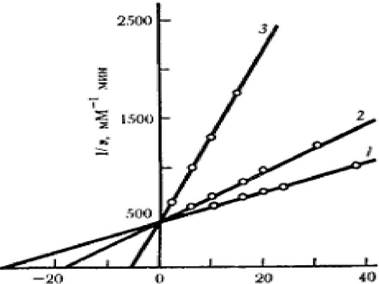
Если отложить экспериментальные данные в координатах (КМ(Каж), [I]), константу конкурентного ингибирования Кi можно определить по формуле 2.33:
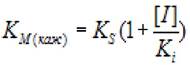 (2.33)
(2.33)
где Км - константа Михаэлиса; [I] - концентрация ингибитора; кs - константа диссоциации фермент - субстратного комплекса; ki - константа диссоциации комплекса фермент - ингибитор.
2.5.2.2 Полное неконкурентное ингибирование (α —> 1, β =0). В этом случае, скорость ХФР определяется уравнением:
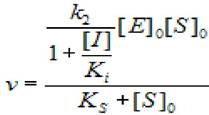 (2.34)
(2.34)
где [S]0 - начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; [I] - концентрация ингибитора; кs - константа диссоциации фермент - субстратного комплекса; к2 - константа диссоциации второй стадии; ki - константа диссоциации комплекса фермент - ингибитор.
Зависимость в координатах Лайнуивера - Берка имеет вид пучка прямых, пересекающихся на оси абсцисс (рисунок 2.5).
Рисунок 2.5 - График зависимости при полном неконкурентном ингибировании
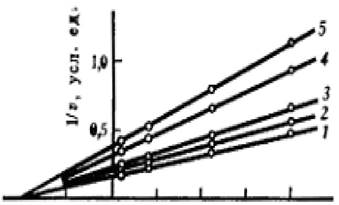
Если представить экспериментальные данные в координатах (1/kkat, [I], константу неконкурентного ингибирования К, можно определить, зная величину кк:
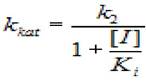 (2.35)
(2.35)
где кк - каталитическая константа; [I] - концентрация ингибитора; к2 - константа диссоциации второй стадии; кi - константа диссоциации комплекса фермент - ингибитор.
2.5.2.3 Бесконкурентное ингибирование (α = β ≤ 1). В этом случае скорость ХФР:
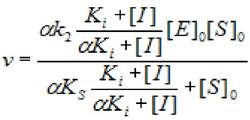 (2.36)
(2.36)
где [S]0 - начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; [I] - концентрация ингибитора; кs - константа диссоциации фермент - субстратного комплекса; к2 - константа диссоциации второй стадии; кi - константа ингибирования; α - коэффициент изменения скорости первой стадии; β - коэффициент, изменения скорости второй стадии.
Значения констант kkat и КМ(каж) ферментативной реакции при увеличении концентрации эффектора уменьшаются в одинаковой степени, поэтому графики в
координатах Лайнуивера - Берка имеют вид семейства параллельных прямых (рисунок 2.6).
Рисунок 2.6 - График зависимости при бесконкурентном ингибировании Для анализа уравнения выражение для каталитической константы
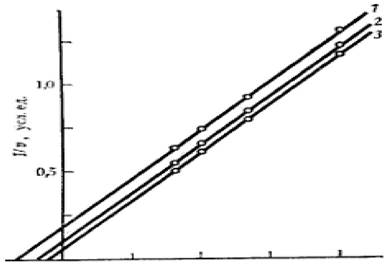
![]() (2.37)
(2.37)
где кк - каталитическая константа; [I] - концентрация ингибитора; к2 - константа диссоциации второй стадии; кi - константа ингибирования; α - коэффициент изменения скорости первой стадии, удобно преобразовать к следующему виду:
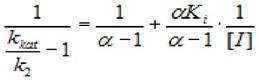 (2.38)
(2.38)
где кк - каталитическая константа; [I] - концентрация ингибитора; к2 - константа диссоциации второй стадии; кi - константа ингибирования; α - коэффициент изменения скорости первой стадии.
Из графика, построенного в координатах (1/(kkat/k2 -1), 1/[I]), можно раздельно найти значения α и Кi).
2.5.2.4 Неконкурентная активация (α = 1, β >1). В этом случае субстрат и активатор связываются независимо с активны центром, образуя тройной комплекс (фермент - субстрат - активатор), что приводит к увеличению скорости образования продукта ХФР. Поэтому начальная скорость ХФР определяется выражением:
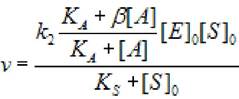 (2.39)
(2.39)
где [S]0 - начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; [А] - концентрация активатора; кs - константа диссоциации фермент - субстратного комплекса; к2 - константа диссоциации второй стадии; кА - константа активирования; β - коэффициент, изменения скорости второй стадии.
Зависимость в координатах Лайнуивера - Берка имеет вид пучка прямых, пересекающихся на оси абсцисс.
2.5.2.5 Смешанные типы ингибирования и активации (α ≠ 1, β ≠ 1). В случае смешанных типов ингибирования или активации графики в координатах Лайнуивера - Берка имеют вид пучка прямых, соответствующих различным концентрациям эффектора, и пересекающихся в общей точке в правом верхнем, левом верхнем или левом нижнем квадранте в зависимости от значений α и β (рисунок 2.7).
Рисунок 2.7 - Графики зависимости при смешенном типе ингибирования
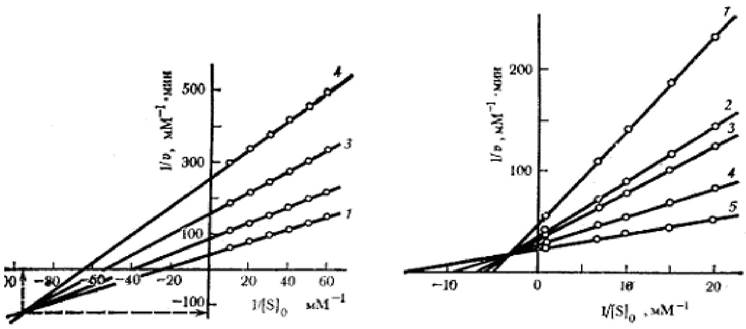
Координаты точки пересечения пучка прямых определяется значениями констант α и β.
Контрольные вопросы по изучаемой теме
1. Какие могут быть варианты взаимодействия фермента с эффектором?
2. Что обозначает обратимое ингибирование?
3. Что обозначает не обратимое ингибирование?
4. Что обозначает конкурентная активация?
5. Что обозначают коэффициенты α и β?
6. Как будет выглядеть график зависимости при смешенном типе ингибирования?
7. Как будет выглядеть график зависимости при неконкурентной активации?
8. Как будет выглядеть график зависимости при бесконкурентном ингибировании?
9. Как будет выглядеть график зависимости при полном неконкурентном ингибировании?
10. Как будет выглядеть график зависимости полном конкурентном ингибировании?
2.6 Ингибирование и активация избытком субстрата
2.6.1 Механизмы ингибирования субстратом
Для многих ферментов установлено, что при добавлении избытка субстрата скорость катализируемой реакции далее не увеличивается и не остается постоянной при концентрации выше насыщающей, а понижается, т. е. развивается ингибирование. Это явление было названо ингибированием избытком субстрата.
Что касается его механизмов, можно предложить пять различных типов ингибирования:
1) субстрат связывается с ферментом двумя или более группами, и только субстрат, связанный таким образом, может принимать участие в реакции. Если присутствует много молекул субстрата, то может возникнуть такая ситуация, что на одном связывающем центре фермента связывается одна молекула субстрата, в то время как на другом участке связывается другая молекула субстрата вместо того, чтобы взаимодействовать с другой группой первой молекулы субстрата. Так как в реакции может принимать участие только молекула, связанная с ферментом двумя точками, молекула фермента, удерживающая две молекулы субстрата, будет неактивна, т. е. будет развиваться ингибирование;
2) при высокой концентрации субстрат может связываться с другим участком, отличающимся от активного центра белка. В этом случае он может ’'неконкурентно’' ингибировать скорость распада субстрата, связанного в активном центре;
3) фермент требует для проявления активности присутствия необходимого активатора. Если субстрат способен образовывать комплекс с активатором, избыток субстрата удаляет активатор, таким образом уменьшая активность фермента;
4) для реакции с двумя или несколькими субстратами избыток одного из субстратов способен связываться с участком связывания другого, ингибируя реакцию;
5) увеличение концентрации субстрата выше определенного предела неспецифически ингибирует реакцию вследствие увеличения ионной силы.
2.6.2 Кинетический анализ ХФР при ингибировании субстратом
Для многих ферментов зависимость v от [S]0можно количественно описать, исходя из предположения об образовании тройного комплекса ES2, не обладающего ферментативной активностью:
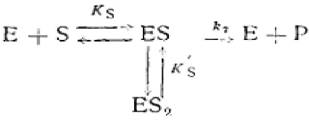 (2.39)
(2.39)
где Е - фермент; S - субстрат; Р - продукт реакции; ES - фермент - субстратный комплекс; ES2 - тройной фермент - субстратный комплекс; Ks'— константа диссоциации тройного фермент — субстратного комплекса; к2 - константа диссоциации второй стадии.
В этом случае уравнение скорости ферментативной реакции будет иметь вид:
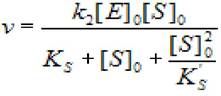 (2.40)
(2.40)
где [S]0 - начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; Ks - константа диссоциации фермент - субстратного комплекса;
к2 - константа диссоциации второй стадии.
Анализ уравнения разбивают на две части:
1) при низких концентрациях субстрата ([S]02«Ks') уравнение (2.40) упрощается до классического уравнения Михаэлиса - Ментена (не наблюдается ингибирование субстратом). Построением графика в координатах Лайнуивера - Берка находим к2 и Ks;
2) при высоких концентрациях субстрата ([S]0» Ks) уравнение (2.40) примет вид:
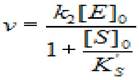 (2.41)
(2.41)
где v - скорость ХФР; [S]0- начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; Ks - константа диссоциации фермент - субстратного комплекса; Ks'— константа диссоциации тройного фермент — субстратного комплекса; к2 - константа диссоциации второй стадии.
Уравнение (2.41) можно привести к виду:
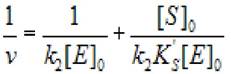 (2.42)
(2.42)
и построив зависимость 1/v от [S]0, найти значения к2 и Ks'. Если в обеих областях найденные значения к2 совпадают, значит схема (2.39) применима для формального описания кинетики изучаемой ферментативной реакции.
Во второй модели тройной комплекс ES2 обладает активностью, но меньшей по сравнению с фермент-субстратным комплексом ES (β<1).
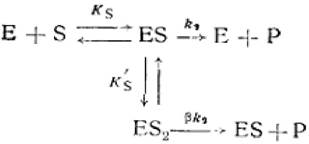 (2.43)
(2.43)
где Е - фермент; S - субстрат; Р - продукт реакции; ES - фермент - субстратный комплекс; ES2 - тройной фермент - субстратный комплекс; β - коэффициент, изменения скорости второй стадии; Ks'— константа диссоциации тройного фермент — субстратного комплекса; к2 - константа диссоциации второй стадии.
В этом случае скорость ферментативной реакции при установившемся равновесии и [S]0» [Е]0 будет описываться уравнением:
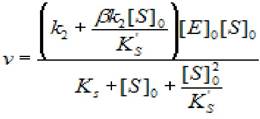 (2.44)
(2.44)
где v - скорость ХФР; [S]0- начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; Ks - константа диссоциации фермент - субстратного комплекса; Ks'— константа диссоциации тройного фермент — субстратного комплекса; β - коэффициент, изменения скорости второй стадии; к2 - константа диссоциации второй стадии.
Обработка схемы также разбивается на две области. При низких концентрациях субстрата определяем к2 и Ks. При высоких концентрациях уравнение упрощается до зависимости:
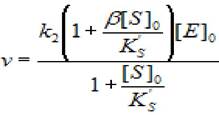 (2.45)
(2.45)
где v - скорость ХФР; [S]0- начальная концентрация субстрата; [Е]0 - концентрация фермента в начале реакции; Ks - константа диссоциации фермент - субстратного комплекса; Ks'— константа диссоциации тройного фермент — субстратного комплекса; β - коэффициент, изменения скорости второй стадии; к2 - константа диссоциации второй стадии.
Построив график в координатах (1/(1 -кэфф/к2), 1/[S]0) для высоких концентраций субстрата найдем значения β и Кs'.
Третий тип субстратного ингибирования, когда к фермент-субстратному комплексу присоединяется несколько молекул субстрата, переводя его в неактивное состояние.
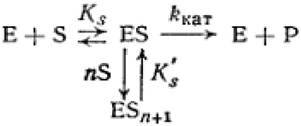 (2.46)
(2.46)
где Е - фермент; S - субстрат; Р - продукт реакции; ES - фермент - субстратный комплекс; ESn+2- комплекс фермент - субстрат - 2 и более молекул; n - количество молекул субстрата, связанных с ферментом; Ks'- константа диссоциации тройного фермент — субстратного комплекса; ккат - каталитическая константа или константа диссоциации второй стадии.
Для анализа подобных случаев разработан графический способ, позволяющий определить число молекул субстрата в неактивном фермент-субстратном комплексе. Обработка экспериментальных данных в этих случаях проводится следующим образом:
1) по графику в координатах (v, lg[S]0) определяем [S]opt;
2) при различных n по формуле (83) находим произведение KSKS';
3) для каждого n строим график в координатах (1/[S]0 + [S]onKsKs', 1/v). Значение n, при котором график линеен, соответствует зависимости (2.44), и, следовательно, модели (2.45) с найденным значением n.
Мы рассмотрели 3 схемы возможного ингибирования ферментативной активности избытком субстрата. Чтобы выбрать механизм ингибирования, сначала надо построить зависимость экспериментально найденных значений скорости в координатах (v, lg[S]0).
Симметричный вид полученной колоколообразной кривой указывает на отсутствие ферментативной активности комплекса SES (рисунок 2.8).
Рисунок 2.8 - Зависимость в координатах для всех моделей ингибирования субстратом

Если же правая ветвь графика (при больших концентрациях субстрата) более пологая по сравнению с левой ветвью, это говорит о ферментативной активности
тройного комплекса (0 <β <1). Если же субстрат ингибирует ферментативную активность, то правая часть графика будет более крутой.
2.6.2 Активация субстратом
В некоторых случаях при увеличении концентрации субстрата скорость ферментативной реакции превышает теоретическую максимальную скорость ХФР, рассчитанную из данных, полученных при использовании небольших концентраций субстрата. Простейшая модель такой активации соответствует схеме, в которой β>1. Анализ экспериментальных данных проводится аналогично (2.43). Единственное отличие заключается в том, что удобнее строить график в координатах (1/(кэфф/к2-1), 1/[S]0) согласно зависимости:
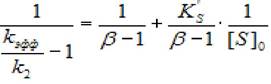 (2.47)
(2.47)
где [S]0 - начальная концентрация субстрата; Ks - константа диссоциации фермент - субстратного комплекса; Ks'— константа диссоциации тройного фермент —субстратного комплекса; β - коэффициент, изменения скорости второй стадии; к2 - константа диссоциации второй стадии.
Контрольные вопросы по изучаемой теме
1. Какие существуют варианты взаимодействия между ферментом и избытком субстрата?
2. Напишите схему реакции при ингибирование избытком субстрата с образованием тройного комплекса субстрат - фермент -субстрат?
3. Как найти скорость ХФР в этом случае?
4. Напишите схему реакции при активации субстратом.
5. Как определить кинетические параметры ХФР в этом случае?
2.7 Факторы, влияющие на ферментативную активность. Влияние pH и температуры на кинетику ферментативных реакций
2.7.1 Факторы, влияющие на ферментативную активность
На каталитическую активность ферментов влияют многие факторы, которые могут изменять строение или химическую природу ферментов. К числу таких факторов относятся:
1) pH;
2) температура;
3) силы, действующие в текучих средах (гидродинамические силы, гидростатическое давление и поверхностное натяжение);
4) химические агенты (спирт, мочевина или пероксид водорода);
5) облучение (свет, звук, ионизирующая радиация).
Иногда снижение каталитической активности, вызванное, например, изменением pH, обратимо. В таких случаях возврат к первоначальным условиям сопровождается восстановлением активности фермента. В известном смысле такая ситуация аналогична рассмотренному случаю обратимого ингибирования. Небольшие изменения одного из перечисленных выше факторов, только слегка сдвигают равновесие (или квазистационарное состояние), характерное для данной ферментативной реакции. В общем случае отклонение от условий, типичных для биологического окружения нативного фермента, должно быть относительно небольшим (или кратковременным). В противном случае возрастает вероятность инактивации фермента.
2.7.2 Обратимое влияние температуры на каталитическую активность фермента
Граница между "обратимой" и "необратимой" инактивацией белков не всегда четко определена. Например, подвергнутый кратковременному нагреванию фермент при охлаждении до свойственной ему "рабочей" температуры может полностью восстановить свою активность. С другой стороны, более продолжительное нагревание при той же температуре или столь же кратковременная термообработка при более высокой температуре могут привести к тому, что при последующем охлаждении активность фермента восстановится лишь частично. Такое поведение белков - ферментов становится понятным, если учесть связь между их строением и функцией, влияние молекулярной динамики на функцию белка и возможность разрыва некоторых слабых связей в нативной структуре фермента при изменении условий среды.
При высокой температуре, когда начинает доминировать процесс термической инактивации фермента, нарушаются зависимости скорости реакции от температуры.
Так ферментативные реакции имеют колоколообразную зависимость скорости реакции от температуры, что объясняется наложением двух эффектов - возрастанием скорости реакции при увеличении температуры и ускорением тепловой денатурации белковой молекулы, приводящей к инактивации фермента при высоких температурах. Денатурация большинства белков начинается в диапазоне температур от 45° С до 50° С и завершается очень быстро при 55° С.
2.7.3 Влияние pH на кинетику ферментативных реакций в растворах
Ферменты, как и все белки, состоят из аминокислот. В зависимости от pH радикалы некоторых аминокислот, а значит, и белок в целом могут приобретать заряд. Заряженные группы часто входят в состав активных центров ферментов, так как в основе целого ряда механизмов ферментативного катализа лежит катализ
кислотного или основного типа. Необходимым условием для осуществления кислотного или основного катализа может быть наличие определенного заряда на ионизируемых группах активного центра. Отсюда следует, что каталитически активная форма фермента существует только в одном строго определенном состоянии ионизации, и в зависимости от pH в нее может превращаться большая или меньшая часть всего имеющегося в смеси фермента (рисунок 2.9).
Рисунок 2.9 - Зависимость активности ферментов от pH
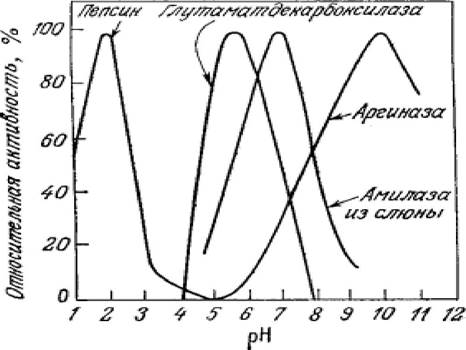
При значениях pH, значительно отличающихся от оптимальных, происходит нарушение сил, стабилизирующих конформацию нативного белка - фермента, что может привести к его денатурации - утрате третичной конформации, и соответственно потери каталитической активности. В этом случае даже после восстановления оптимального pH ренатурация фермента становится маловероятной.
Контрольные вопросы о изучаемой теме
1. Какие факторы влияют на ферментативную активность?
2. Влияние pH на кинетику ферментативных реакций в растворах.
3. Как изменяется скорость ХФР при изменении температуры?
4. Какие процессы происходят при денатурации в структуре фермента?
5. Что такое ренатурация?