Принципы структурной организации белков - Г. Шульц 1982
Эволюция белков
Обнаружение отдаленных родственных связей
Сравнение аминокислотных последовательностей
Априорная значимость является верхней границей значимости родства. Аналогия между двумя отдаленно родственными белками не всегда очевидна, и для ее нахождения нужны эффективные критерии. В качестве примера рассмотрим a-цепи гемоглобина человека и миоглобин спермы кашалота, сопоставленные Дейхофом [20] при пренебрежении вставками и делециями. В этом случае длина совмещаемой цепи составляет 142 остатка, 37 из которых идентичны. «Априорная вероятность» нахождения общих остатков в любой из 37 позиций этих цепей очень мала:
![]()
И напротив, наблюдение такого подобия свидетельствует о том, что оно не может быть случайным и что имеет большую значимость. Соответственно «априорную значимость» определяют как величину, обратную «априорной вероятности». Высокая значимость подобия для биологических объектов указывает на эволюционное родство.
Биологические ограничения заметно снижают априорную значимость. Априорная вероятность является математическим понятием. Чтобы получить более реальные значения, следует учесть биологические ограничения. Так, не все аминокислоты встречаются с одинаковой частотой (табл. 1.1), в связи с чем вероятность появления данного остатка в данном положении не будет составлять 1/20 для каждого из остатков. Кроме того, все остатки представляют собой составные элементы вполне определенной трехмерной структуры. Например, заряженный остаток, как правило, не может находиться внутри белка. Это повышает вероятность нахождения других остатков в этой области от 1/20 до более высокого значения.
Биологические ограничения отражены в относительной частоте замен. Наилучшим образом эти ограничения можно учесть путем проведения анализа на основе экспериментальных данных по природным белкам. Для этой цели можно использовать матрицу частот относительных замен (табл. 1.2). Элементы этой матрицы представляют отношение частоты наблюдаемых аминокислотных замен к частоте, ожидаемой при случайных заменах для данного распределения частот встречаемости аминокислот (табл. 1.1). Поэтому эти элементы в среднем отражают природные ограничения, налагаемые на замены аминокислот.
При выявлении подобия двух последовательностей с помощью этой матрицы ответ для некоторого положения последовательности получают не в виде «да» (подходит) или «нет», а в более «сравнительной» форме: замена Ilе ↔ Ilе происходит с высоким уровнем значимости, а Ilе ↔ Val (часто встречающаяся замена), Ilе ↔ Thr и Ilе ↔ Arg отвечают последовательно понижающимся абсолютным величинам элементов матрицы (табл. 1.2). Элементы, отвечающие всем положениям последовательности, можно сложить и сопоставить со случайными последовательностями. При этом необходимо предусмотреть, чтобы частота встречаемости аминокислот в случайных последовательностях была той же самой, что и в рассматриваемых белках. С помощью этой схемы можно обнаружить родство двух совершенно различных последовательностей, содержащих большое число вероятных замен. И напротив, последовательности с 15% идентичности и с большим числом маловероятных замен следует рассматривать как неродственные.
Эта схема была предложена Мак-Лахланом [598]. Он преобразовал матричные элементы m(і, j) табл. 1.2 в целые числа от 0 до 7 путем пропорционального уменьшения всех недиагональных элементов до уровня 0—5. Диагональные элементы оказались равными 6 и 7, что отражает ненамного большую значимость идентичности остатков по сравнению с часто встречающимися заменами. Для получения критерия подобия матричные элементы mr(i, j) для каждого положения r цепи, содержащей аминокислоту і в одной цепи и аминокислоту j в другой, суммируют. В пашем примере (миоглобин и a-цепь гемоглобина) этот критерий равен сумме:
![]()
Затем методами комбинаторики рассчитывают распределение всех сумм М, ожидаемое для случайных последовательностей с той же самой частотой встречаемостей аминокислот (см. работу [598]). Этот расчет заметно облегчается благодаря использованию в качестве элементов mr(i, j) небольших целых чисел.
Поскольку основной интерес заключается не в вероятности получения самих сумм М, а в вероятности того, что полученная сумма М будет означать родство, необходимо сравнивать совокупную вероятность (сумму всех вероятностей) всех сумм, больших или равных М, с совокупной вероятностью всех сумм, меньших М. Последняя кумулятивная вероятность может быть положена равной 1,0, поскольку представляют интерес только высокие значения М, т. е. низкие кумулятивные вероятности всех сумм, больших или равных М, и поскольку сумма обоих типов кумулятивных вероятностей равна 1,0. Распределение кумулятивных вероятностей всех сумм, больших или равных М, приведено на рис. 9.5. При сравнении миоглобина кашалота с a-цепью гемоглобина человека эта кумулятивная вероятность достигает 2 ∙ 10-9 [598], что на восемь порядков больше рассчитанной выше априорной вероятности.
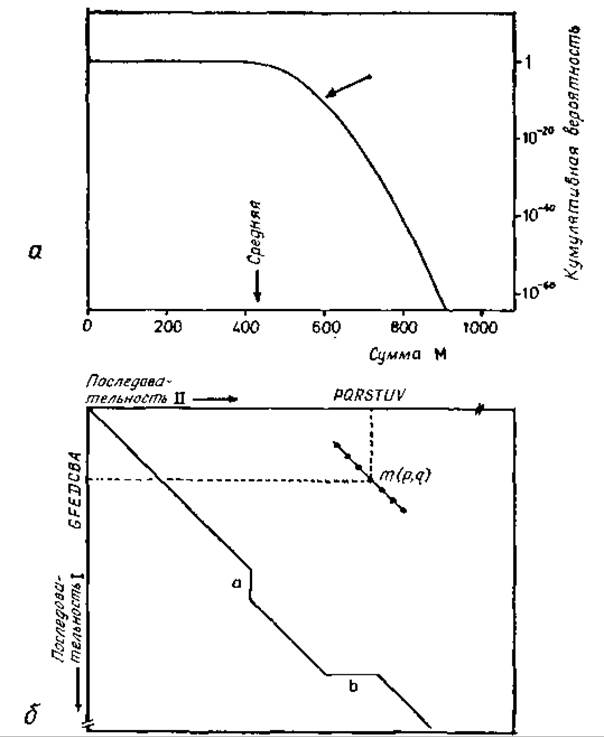
Рис. 9.5. Сравнения аминокислотных последовательностей. а — распределение кумулятивных вероятностей всех сумм, больших или равных М, для случайных последовательностей в цепях, состоящих из 142 остатков [598]. О расчете М см. текст. Сумма и соответствующая кумулятивная вероятность для сравнения миоглобина кашалота и a-цепи гемоглобина человека указаны стрелкой, б — схема матрицы сравнения двух последовательностей I и II [598]. Оба отрезка ABCDEFG и PQRSTUV имеют длину 7 и при сравнении дают одни элемент матрицы. Диагональ показывает корреляцию между последовательностями, которая выявляет вставки в последовательности I в положении а и в последовательности II в положении.
Метод Мак-Лахлана дает стандартную значимость для родства двух последовательностей. Поскольку кумулятивная вероятность учитывает биологические ограничения, налагающиеся на замену аминокислот (хотя и в весьма обобщенном виде), она намного более достоверна, чем априорная вероятность. Такую биологически согласованную вероятность называют «стандартной вероятностью», а обратную ей величину — «стандартной значимостью» [387]. Уровень, выше которого стандартная значимость означает эволюционное родство, не является достаточно четким. Ясно, что для величин, бoльших 100, такое родство может рассматриваться как рабочая гипотеза. В принципе высокая стандартная значимость может исключить случай конвергентной эволюции, так как конвергенция определяется биологическими ограничениями, а они уже были учтены. В действительности, однако, никогда нельзя быть уверенным, что все ограничения известны.
Матрица сравнения может помочь в правильном расположении последовательностей. Рассчитанная выше стандартная значимость предполагает точное совпадение без вставок и делений, что мало вероятно в случае такого большого эволюционного расстояния, как между миоглобином и гемоглобином. Чтобы каким-то образом учесть вставки и делеции, необходимо произвести сдвиги определенных участков последовательности. Однако такие сдвиги увеличивают вероятность высоких значений суммы М, поскольку поиск хорошего соответствия осуществляется автоматически. Поэтому исходное распределение вероятностей (рис. 9.5, а) применять уже нельзя.
В этом случае прежде всего необходимо локализовать вставки и делеции. Для этой цели выбирают последовательность конечной длины (например, из семи остатков) и предполагают, что внутри ее не происходит сдвигов (т. е. вставок и делеций). Затем совмещают все возможные пары (р, q) нарушений, относящихся соответственно к положению р первой цепи и к положению q второй цепи. Каждая суперпозиция дает сумму М(р, q), как показано на рис. 9.5, б. Эту сумму (или соответствующие обозначения) вносят в матрицу сравнения (рис. 9.5, б). В этой матрице линии высоких значений сумм означают наилучшее совпадение, нарушения этих линий указывают на вставки или делеции.
После установления совпадения по матрице, показанной на рис. 9.5, б, можно рассчитать с помощью процедуры, описанной выше для сравнения миоглобина с гемоглобином, кумулятивные вероятности, а следовательно, стандартную значимость родства.
Качественный критерий родства можно вывести из наблюдаемого распределения сумм М. Очень часто, однако, явного совпадения обнаружить не удается. В таких случаях наблюдаемое распределение всех значений М(р, q) (20 000 при сравнении цепи из 100 остатков с цепью из 200 остатков) можно сравнить с распределением, ожидаемым при сравнении случайных последовательностей. Если высокие значения М(р, q) встречаются намного чаще, чем можно было ожидать, то в последовательностях имеется много совпадающих участков и белки родственны друг другу. Однако степень этого родства трудно выразить количественно, поскольку стандартная значимость не может быть рассчитана.
Система суммирования исключает ложные признаки. Она может выявить структурные повторения. Поскольку этот метод очень высоко оценивает подобие аминокислот и не придает слишком большого веса их идентичности, он нечувствителен к неправильному выстраиванию, связанному сложной маркировкой остатков, например Тrр-59 и Тrр-56 соответственно в цитохромах с и с551 (разд. 9.5).
Этот метод можно также применять и к сравнениям в пределах одной цепи для поиска повторений, которые могут указывать на дупликацию гена. Такие повторения могут проявляться в виде линий высокой значимости, параллельных диагонали.
В особых случаях, когда можно ожидать высокоупорядоченные повторения, как, например, в коллагене или в тропомиозине, такие упорядоченности можно выявлять с помощью одномерного анализа Фурье [599]. В этом случае каждому типу остатков приписывается определенное число, например от 1 до 20 для аминокислот, расположенных в порядке табл. 1.2. Такое расположение есть одномерное представление вероятностей аминокислотных замен. Пользуясь этим распределением, данную последовательность переводят в непрерывную функцию, высота которой характеристична для свойств данной аминокислоты (очень высокие значения, например, отвечают ароматическим боковым цепям). Затем фурье-преобразование этой функции выявляет периодичности, т. е. повторения аминокислот с аналогичными свойствами.