Принципы структурной организации белков - Г. Шульц 1982

Статистическая механика перехода спираль - клубок
Модель Зимма - Брэгга для перехода спираль - клубок

Член, учитывающий взаимодействие ближайших соседей, вводится в упрощенную формулу. Зимм и Брэгг [789] применили модель Айзинга к переходу спираль — клубок гомополипептидных цепей. Для этой цели они разделили конформационное пространство на две области аR или «а», но не a_R или «клубок». Кроме того, они использовали приближенное уравнение (А.4), не учитывающее взаимодействия остаток — остаток, а затем ввели член, учитывающий взаимодействие между ближайшими соседями. Для цепи, состоящей из N остатков данного типа, уравнение (А.4) принимает вид:

После перемножения получаем сумму 2^N слагаемых

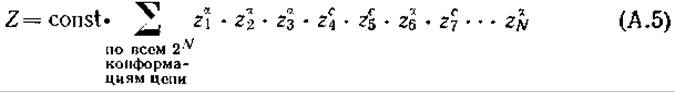
Для каждого возможного сочленения спираль — клубок и клубок — спираль вводится дополнительный множитель

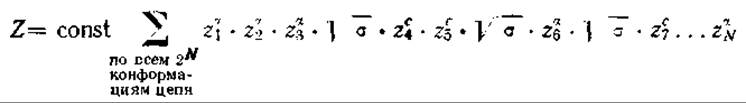
Это можно выразить в форме

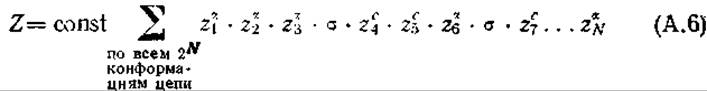
путем попарного объединения множителей и использования их только для сочленении спираль — клубок. Это допустимо, поскольку а-сегментов столь же много, как и клубковых сегментов; в том случае, если один структурный тип превосходит по числу сегментов другой, различиями пренебрегают.

Множитель а приводит к отрицательным результатам, если сочленений слишком много, и отдает предпочтение протяженным сегментам идентичной конформации. Это — альтернативное описание «кооперативности остатков идентичной конформации», или в данном случае «кооперативности остатков спиральной конформации». Можно также говорить о выгодности «нуклеаций клубка или спирали». Поэтому величину а называют «параметром неоперативности или нуклеации».