Принципы структурной организации белков - Г. Шульц 1982
Предсказание вторичной структуры по аминокислотной последовательности
Физико-химические методы
Методы, основанные на статистической механике
Физико-химические методы в отличие от вероятностных основываются не только на известных корреляциях между аминокислотной последовательностью и структурой в базовом наборе глобулярных белков, а используют также другие экспериментальные и теоретические данные. Эти методы можно подразделить на применяющие стереохимический анализ и статистическую механику. В приложении рассмотрены некоторые важные аспекты статистики полипептидных цепей, необходимые для понимания методов статистической механики и физических основ укладки цепи.
Расчеты энергии
Статистические веса можно рассчитать на основании геометрии и вандерваальсовых сил. Идея использования для предсказания методов статистической механики наиболее широко разрабатывалась Шерагой и сотрудниками. Котельчук и Шерага [363, 364] основывали свои предсказания на упрощенном методе, описанном в приложении при выводе уравнения (А.4). Они рассчитали статистические веса zaR , zaL и zsε для каждого остатка* кроме Gly и Pro, которые были рассмотрены отдельно. В расчетах они учитывали вандерваальсовы взаимодействия (гл. 3) между различными частями цепи. Поскольку рассматривалась система, состоящая из цепи и растворителя, был включен также член, учитывающий вклад свободной энергии растворителя. Для каждого остатка конформация с наибольшей величиной z принята за его склонность (табл. 6.1). Поскольку предпочтения состояния аL обнаружено не было, то выявились только «спиральные» (≡аR) и «случайные» (клубок ≡ не аR) склонности. Отметим, что сделанные с помощью этих расчетов оценки хорошо согласуются с экспериментальными данными по синтетическим полипептидам [328] и с эмпирическими данными, типа триплета в базовом наборе. Затем средние значения всех углов ∅, ψ’ найденные в четырех позициях таблицы, используются в качестве предсказанных величин (∅, ψ) для положения i'-го остатка цепи, свернутой общим для данной группы белков образом.
* Статистические веса zaR, zaL a zε — значения вероятности того, что данный остаток принимает в основной цепи конформацию, находящуюся соответственно в аR-, aL- и ε-(растянутая цепь)-областях. Эти области определены на рис. 2.3.
полученными из рассмотрения базового набора по глобулярным белкам (табл. 6.1).
Расчет спиральных потенциалов по склонностям может учитывать кооперативность. Исходя из склонностей, Котельчук и Шерага [364] предложили простой алгоритм предсказания, согласно которому спирали инициируются в том случае, когда располагаются подряд четыре остатка со склонностью к спирали; спирализация в сторону С-конца продолжается до тех пор, пока процесс не затормаживается двумя последовательно расположенными остатками со склонностью к беспорядочному свертыванию. Направленное наращивание явилось следствием расчетной схемы, согласно которой влияние данного остатка на соседа осуществлялось только в направлении С-конца, но не N-конца. Использование такого алгоритма предполагает отказ от простой схемы невзаимодействующих остатков уравнения (А.4). Вводятся инициация спирали и ее роста и тем самым в неявном виде учитывается взаимодействие между соседними остатками.
Идея инициации спирали четырьмя остатками и рост спирали в одном направлении вплоть до появления двух последовательных остатков с тенденцией встраиваться в беспорядочный клубок была также использована Леберманом [365], который несколько модифицировал методику для получения лучшего соответствия в базовом наборе.
Эмпирическая функция распределения
Склонности остатков образовывать спирали, основанные на частотах встречаемости и найденные с помощью эмпирических функций, эквивалентны. Поскольку объем данных о структуре глобулярных белков в настоящее время уже достаточно велик, становится возможным нахождение статистических весов zaR и zε по уравнению (А. 4). Для этой цели Бэджисом и сотр. [31] уравнение (А.4) было представлено в виде:
![]()
где χ = aR или в; очень малой величиной пренебрегали. Интеграл в скобках представляет собой вероятность того, что у рассматриваемого остатка будут наблюдаться данные углы — и ψ на карте (—, ψ) (рис. 2.3). Это есть не что инcе, как распределение Больцмана, усредненное по всем ориентациям боковой цепи. Поскольку функция Е(—, ψ, χ) не известна с достаточной точностью, рассчитать распределение вероятностей невозможно. Однако они должны коррелироваться с наблюдаемыми частотами встречаемости остатков данного типа на карте (∅, ψ) (рис. 2.4). Поэтому выражение в скобках можно удовлетворительно описать непрерывной функцией — и ψ, подогнанной к наблюдаемым частотам встречаемости. Такие эмпирические функции могут быть затем использованы для расчета интеграла (6.1) по (аR- и ε-областям, что дает вероятность или частоту встречаемости aR и ε-конформаций zaR и zε. Полученные таким способом величины zε приведены в табл. 6.2*. Однако основанный на статистической механике подход к определению склонности остатка принимать то или иное конформационное состояние в действительности близок к чисто статистическому анализу.
Описанный выше способ не позволяет определять склонности к поворотам цепи, поскольку при соответствующих конформациях углы (∅, ψ) остатков не находятся в определенной области, а рассеяны по карте (∅, ψ). Для этого случая Бэджис и сотр. [31] избрали статистический подход Льюиса и сотр. [326], использовав расширенный базовый набор.
Склонности нонапептидов были использованы для нахождения потенциала центрального остатка встраиваться в спираль. При предсказаниях вторичной структуры Шерага и сотр. [31, 366] рассмотрели комбинации склонностей остатков от і — 4 до i + 4 и применили их для расчета аR-, ε- и rt-потенциалов (см. определение в разд. 6.1) остатка і. Причина рассмотрения именно девяти остатков связана с тем обстоятельством, что, согласно более ранним энергетическим расчетам [367], нонапептид представляет как раз тот фрагмент, который существенно определяет конформацию центрального остатка. Затем для всех сегментов, включающих более четырех остатков, была предсказана конформация спирали (≡aR), если aR-потенциал был выше, чем ε- и rt-потенциалы, а также больше порогового значения. Этот порог был определен как средневзвешенное по всем aR-потенциалам цепи. Таким же способом были сделаны ε- и rt-предсказания.
Модель Зимма — Брэгга в применении к гетерополимерам
Модель Зимма — Брэгга применима к природным белкам. Алгоритм предсказания спирали, основанный на модели Зимма — Брэгга, был предложен Льисом и сотр. [368, 369]; при этом в уравнении (А.9) учитываются индивидуальные относительные статистические веса si для каждого положения і цепи в отличие от равенства всех величин si в уравнении (А.8) для гомополимера. Вероятность Pi нахождения остатка в положении і в а-конформации задается выражением:
![]()
* В табл. 6.2 ε-склонности обозначены как ß-склонности. Шерага и сотр. отметили, что можно предсказать только ε-, а не ß-структуру, поскольку конформация остова не определяет полностью водородных связей.
с помощью которого из всех возможных 2N конформаций цепи отбираются только те, которые являются спиральными в положении і (уравнение (А.6)). Нормирование выполняется, как обычно, путем деления на Z, характеризующую распределение возможных конформационных состояний полипептидной цепи (разд. А.1). В качестве примера получим Р1 для случая N — 2 (см. уравнение (А.7)):
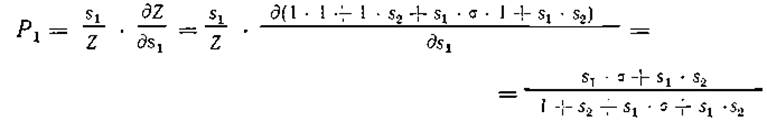
Остатки с низкими относительными статистическими весами значительно укорачивают среднюю длину спирали. Чтобы оценить спиральный потенциал данного белка, было использовано одно значение параметра инициации σ = 5 ∙ 10-4 (разд. А.4). Кроме того, были введены три различные значения s для всех типов остатков. Так, s = 0,385 соответствовало остаткам, прерывающим спираль (В), s = 1, 00 — индифферентным к спирали (I) и s = 1,5 — образующим спираль (Н)(табл. 6.1)*. Значения σ и s получают по наклонам и температурным переходам зависимостей, описывающих переходы спираль — клубок в синтетических полипептидах, используя уравнения (А. 18) и (А.20). Спиральная конформация предсказывается для всех положений остатков i, для которых Pi больше средней величины Pi. В результате получаются непрерывные потенциальные функции, поскольку уравнение (6.2) учитывает кооперативность модели Зимма — Брэгга, согласно которой спирали должны иметь определенную длину (рис. А. 1). Этот метод предсказания дает спиральные сегменты длиной около 10 остатков, что намного меньше длины, ожидаемой для данного значения а гомополимеров при s = 1, т. е. ![]() (уравнение (А. 17)).
(уравнение (А. 17)).
Такое укорочение спирали является следствием включения остатков с низкими значениями s.
Модифицированная модель Зимма—Брэгга. Аналогичным образом модель Зимма—Брэгга была применена Птицыным и сотр. [370], которые использовали для всех типов остатков один параметр инициации σ = 5 ∙ 10-4 и шесть различных значений si, базирующихся на экспериментальных данных по синтетическим полипептидам. Значения si остатков, для которых отсутствовали экспериментальные данные, были выбраны по методу Льюиса и сотр. [368]. В последующих работах [371—374] для определения величин s (табл. 6.1) привлекались также стереохимические данные. Модель Зимма — Брэгга была модифицирована путем учета влияния соседних остатков (например, остатков і и і + 3 в а-спирали). Кроме того, авторы ввели индивидуальные значения о для каждого типа остатка и расширили алгоритм, сделав попытку предсказать уже не две (спираль и клубок), а до шести различных конформаций.
Параметры Зимма—Брэгга, полученные из данных по глобулярным белкам и синтетическим полипептидам
* Как отмечено в разд. А. 2, относительные статистические веса s соответствуют склонностям. В уравнении (А.8) s есть склонность к спирализации.
Вероятностный характер метода предсказания Чоу и Фасмана; учет кооперативности. Метод предсказания Чоу и Фасмана [201, 340] во многих отношениях основывающийся на модели Зимма — Брэгга, имеет вероятностную природу. Авторы определяли склонности к a-, ß- и rt-конформациям по частотам встречаемости в базовом наборе. Для заданной аминокислотной последовательности они последовательно проанализировали точки инициации а- и ß-конформаций путем комбинирования соответственно а- и ß-склонностей в гекса- и пентапептидах. От каждой найденной точки инициации затем производилось наращивание цепи в обоих направлениях до тех пор, пока не встречались остатки с малыми склонностями. Для предсказания реверсивных поворотов авторы пользовались схемой Льюиса и сотр. [326]. Применение метода Чоу и Фасмана описано в разд. 6.3, где приведены дальнейшие подробности.
Склонности к спирали, полученные с помощью статистической механики синтетических полипептидов, соответствуют склонностям, основанным на частотах встречаемости в глобулярных белках. В своих последующих работах Чоу и Фасман [201] сопоставили склонности к спирали, определенные но наблюдаемым частотам встречаемости в глобулярных белках, с данными, полученными на основании температур 0 переходов спираль — клубок синтетических полипептидов, согласно модели Зимма — Брэгга. Как показано в разд. А.5, по температуре перехода θ можно определить относительные статистические веса s, а следовательно и склонности к спиралеобразованию. Чоу и Фасман показали, что величины s семи типов остатков, для которых имеются данные по синтетическим полипептидам, в пределах 10% согласуются со склонностями к спирали, полученными по частотам встречаемости в глобулярных белках. Это соответствие было более подробно исследовано Судзуки и Робсоном [352].
Параметры инициации, полученные из данных по синтетическим полимерам, хорошо коррелируют с частотами встречаемости остатков на концах спирали. Чоу и Фасман [201] сравнили также параметры инициации σ, полученные при рассмотрении переходов спираль — клубок (разд. А.5), с частотами встречаемости остатков на концах спиралей в глобулярных белках. Как и в работах Лифсона и Ройга [375], в данном случае было проведено усреднение по обоим концам спирали. Кроме того, рассматривались частоты встречаемости трех остатков на каждом конце (а не только одного остатка по модели Зимма—Брэгга), поскольку каждый из трех концевых остатков а-спирали образует только одну водородную связь. При сопоставлении найденных частот с шестью значениями о, полученными при изучении переходов спираль — клубок, несмотря на различие абсолютных величин, была обнаружена хорошая корреляция (коэффициент корреляции между логарифмами составлял +0,75). Поскольку переходы беспорядочный клубок — ß-складчатый лист в синтетических полимерах значительно менее изучены, то таких корреляций для ß-структур пока установить не удалось.