Структура и функционирование белков. Применение методов биоинформатики - Джон Ригден 2014
Динамика белков: от структуры к функционированию
Молекулярно-динамические расчеты
Ограничения и улучшенные алгоритмы сэмплирования
Несмотря на то, что молекулярно-динамические расчеты стали цельной частью структурной биологии и неоднократно представляли бесценную возможность взглянуть на биологические процессы на атомарном уровне, в этой области остаются ограничения как методологического характера, так и связанные с вычислительными ресурсами. Методологические ограничения возникают из классического описания атомов и приближения взаимодействия простыми энергетическими термами вместо уравнение Шредингера. Это означает, что химические реакции (разрыв и образование химических связей) не могут быть описаны. Поляризационные эффекты и туннелирование протона также оказываются вне области классических МД расчетов.
Вторая группа ограничений возникает из вычислительных потребностей МД расчетов. Несмотря на то, что связи обычно рассматриваются в качестве пространственных ограничений, налагаемых на атомы, что позволяет исключить наиболее высокочастотные движения, длина шага по времени в МД расчетах, как правило, не может быть выбрана более 2 фс. Наносекундный расчет, следовательно, требует 500 000 кратного вычисления сил и такого же количества шагов интегрирования. При нынешних алгоритмах и вычислительной мощности времена порядка 100 нс оказываются достижимыми после 3-4 недель расчетов для сольватированного белка, имеющего 200 остатков.
Однако биологически важное движение белков, такое как масштабные конформационные переходы, сворачивание или денатурация происходят за времена от микро- до миллисекунд. Таким образом, становится очевидным, что несмотря на все возрастающую производительность вычислительной техники, чей рост можно охарактеризовать как примерно стократный за 10 лет, МД расчеты в обозримом будущем не смогут решить проблему сэмплирования исключительно за счет быстродействия компьютеров. Поэтому специально для решения проблемы сэмплирования конформаций и предсказания функционально значимых движений белков были предложены альтернативные методы, отчасти основанные на МД.
Один из подходов состоит в уменьшении числа частиц. Поскольку белки, как правило, рассматриваются в окружении растворителя, и большая часть моделируемой системы представлена молекулами воды, то создание неявных моделей растворителя является многообещающим способом уменьшения ресурсоемкости вычислений (Still et al. 1990; Gosh et al. 1998; Jean-Charles et al. 1991; Luo et al. 2002). Другим способом уменьшения числа частиц является использование так называемых крупнозернистых (coarse-grained) моделей (Bond et al. 2007), в которых атомы объединены в группы, называемые псевдоатомами (зернами). Например, обычно четыре молекулы воды рассматриваются как один псевдоатом. Такое объединение приводит к двум эффектам: во-первых, сокращается число частиц, а во-вторых, может быть увеличен шаг по времени, который зависит от частоты наиболее быстрых колебаний в системе. Но крупнозернистое представление не ограничивается молекулами воды. Например, аминокислоты могут быть также представлены одним или несколькими зернами. Это позволяет резко снизить требования к ресурсам, делая возможным расчет крупных макромолекулярных агрегатов на временах до микро- и миллисекунд. Этот выигрыш в эффективности, однако, невольно сопровождается проигрышем в точности по сравнению с полноатомным описанием белков, что позволяет получать лишь полуколичественные результаты. Принципиально важным для успешности крупнозернистых моделей является параметризация силовых полей, которые должны быть одновременно и точными, и универсальными, то есть подходить для описания систем различного состава и конфигурации. Чем более крупными являются зерна, тем сложнее процесс параметризации, поскольку более специфические взаимодействия должны быть эффективно учтены в небольшом числе параметров и термов. Это привело к множеству моделей белков, липидов и воды, являющихся различными компромиссами между точностью и универсальностью (см., например, Marrink et al. 2004).
Другие улучшенные методы сэмплирования, основанные на МД расчетах и сохраняющие атомарное представление структуры, включают в себя метод обмена репликами (replica exchange molecular dynamics, REMD) и коллективную динамику (essential dynamics, ED), которые обсуждаются в следующих разделах. Кроме того, обсуждается и ряд не имеющих отношения к МД методов, направленных на предсказание того, каким образом функционируют белки.
9.1.3.1. Метод обмена репликами
Целью большинства работ по компьютерному моделированию био-молекулярных систем является расчет макроскопического поведения исходя из микроскопических взаимодействий. Согласно равновесной статистической механике, любая наблюдаемая величина, которая может быть связана с макроскопическим экспериментом, определяется как среднее по ансамблю всех возможных состояний системы. Однако из-за ограниченных возможностей вычислительного оборудования полностью сошедшееся сэмплирование всех возможных конформационных состояний с соответствующими статистическими весами по Больцману достижимо только для простых систем, содержащих небольшое число аминокислот (см., например, Kubitzki and de Groot 2007). Для белков же, состоящих из сотен и тысяч аминокислот, традиционные МД расчеты зачастую не обладают сходимостью, и по этой причине не может быть проведена надежная оценка экспериментальных величин.
Неэффективность сэмплирования является результатом холмистой поверхности свободной энергии системы - понятия, введенного Фрауэнфельдером (Frauenfelder et al. 1991; Frauenfelder and Leeson 1998). Предполагается, что в целом поверхность является воронкообразной, причем нативные состояния системы заселяют глобальный минимум свободной энергии (Anfmsen 1973).
При более пристальном взгляде видно, что сложная многомерная поверхность свободной энергии характеризуется множеством локальных минимумов с почти одинаковой энергией, которые разделены барьерами различной высоты. Каждый из этих минимумов соответствует одному конкретному конформационному подсостоянию, причем соседние минимумы соответствуют схожим конформациям. В терминах этого наглядного представлення структурные переходы являются преодолением барьеров, причем скорость перехода зависит от высоты барьера. Для МД расчетов при комнатной температуре возможно легкое преодоление только тех барьеров, которые меньше или сравнимы с тепловой энергией квТ, что соответствует лишь небольшим внешним структурным изменениям, например переупорядочиванию боковых цепей. По этой причине система будет проводить большую часть времени в локально стабильных состояниях (кинетический захват, kinetic trapping) вместо перемещения по различным конформационным состояниям. Такое перемещение представляет огромный интерес, поскольку связано с биологической функцией, но требует от системы способности преодолевать высокие энергетические барьеры. К сожалению, поскольку МД расчеты в основном ограничены наносекундным диапазоном, функционально значимые конформационные переходы наблюдаются редко.
Чтобы попытаться найти решение этой проблемы многих минимумов было предложено множество улучшенных методов сэмплирования (см., например, Van Gunsteren and Berendsen 1990; Tai 2004; Adcock and McCammon 2006 и ссылки в них), среди которых можно упомянуть алгоритмы обобщенного ансамбля, широко используемые в последние годы (см. например, обзоры Mitsutake et al. 2001; Iba 2001). Эти алгоритмы сэмплируют искусственный ансамбль, который создается путем комбинаций или вариаций исходного ансамбля. Алгоритмы второй категории (например, Berg and Neuhaus 1991) в основном изменяют исходное колоколообразное распределение импульсов p(V) в системе, вводя так называемый мультиканонический весовой фактор w(V), так что итоговое распределение оказывается постоянным p(V)w(V) = const. Затем это плоское распределение может быть широко сэмплировано методами МД и Монте-Карло, поскольку барьеров потенциальной энергии больше нет. Из-за введенных модификаций оценки средних значений физических величин по каноническому ансамблю должны быть получены с помощью перенормировки (Kumar et al. 1992; Chodera et al. 2007). Основной недостаток этих алгоритмов, однако, состоит в нетривиальном определении различных мультиканонических весовых факторов с помощью итеративного процесса, использующего короткие пробные расчеты. Для сложных систем эта процедура может оказаться очень громоздкой, в связи с чем были предприняты попытки улучшить сходимость итеративного процесса (Berg and Celik 1992; Kumar et al. 1996; Smith and Bruce 1996; Hansmann 1997; Bartels and Karplus 1998).
Метод обмена репликами (replica exchange (REX) algorithm), paзpaботаный как расширение метода имитации отпуска (Marinari and Parisi 1992), устраняет проблему множителей. Он относится к первой категории сэмплируется обобщенный ансамбль, построенный на основе нескольких копий исходного ансамбля. Благодаря простоте и легкости в реализации, этот алгоритм широко использовался в последнее время. Чаще всего используется формулировка алгоритма REX при стандартной температуре (Sugita and Okamoto 1999), причем структура общего гамильтониана в этом алгоритме привлекает все большее внимание (Fukunishi et al. 2002; Liu et al. 2005; Sugita et al. 2000; Affentranger et al. 2006; Christen and van Gunsteren 2006; Lyman and Zuckerman 2006).
В МД расчетах по методу обмена репликами при стандартной температуре (Sugita and Okamoto 1999), обобщенный ансамбль создается из М + 1 невзаимодействующей копии, или реплики; системы в диапазоне температур {Т0,...,ТМ} (Тm≤ Тm+1; m = 0,...,М), что может быть сделано, например, распределением вычислений по М + 1 узлу на компьютере с параллельной архитектурой (Рис. 9.6 слева). Состояние этого обобщенного ансамбля описывается набором состояний S = {...,sm,...}, где sm описывает состояние реплики m, имеющей температуру Тm. Теперь алгоритм состоит из двух последовательных шагов: (а) независимый расчет каждой реплики при постоянной температуре, и (b) обмен репликами S = {...,sm,...,sn,...} → S'= {...,sn',..., sm,...} согласно критерию, подобному критерию Метрополиса. Вероятность принятия обмена задается выражением
![]()
где Vm является потенциальной энергией, а ßm-1 = kBTm. Чередуя шаги (а) и (b) траектория обобщенного ансамбля блуждает в пространстве температур, что в свою очередь приводит к блужданию в пространстве энергий. Это облегчает эффективное и статистически обоснованное конформационное сэмплирование на энергетической поверхности системы даже при наличии большого количества локальных минимумов.
Выбор температуры сильно влияет на производительность алгоритма. Температуры реплик должны быть выбраны так, чтобы а) низшая температура была достаточно малой для эффективного сэмплирования низкоэнергетических состояний, б) высшая темература была достаточно большой для преодоления энергетических барьеров в рассматривамой системе и в) вероятность принятия P(S→S’) была досточно высока, что требует подходящего перекрывания распределений потенциальной энергии для соседних реплик. Для больших систем с явно заданным растворителем это последнее условие является наиболее затруднительным. Простая оценка (Cheng et al. 2005; Fukunishi et al. 2002) показывает, что наибольший вклад в разность свободных энергий ∆V ~ Ndf∆T вносит растворитель, число степеней свободы которого Ndf sol составляет большую долю общего числа степеней свободы системы Ndf. Таким образом, получения разумной вероятности принятия можно достичь лишь сохраняя температурные интервалы ∆T = Tm+1 - Tm малыми (обычно несколько градусов), что резко увеличивает вычислительные требования для систем, имеющих несколько тысяч атомов и более. Несмотря на это жесткое ограничение, алгоритмы REX стали общепризнанным методом для изучения сворачивания и денатурации пептидов (Zhou et al. 2001; Rao and Caflisch 2003; Garcia and Onuchic 2003; Pitera and Swope 2003; Seibert et al. 2005), предсказания структуры (Fukunishi et al. 2002; Kokubo and Okamoto 2004), фазовых переходов (Berg and Neuhaus 1991) и вычисления свободной энергии (Sugita et al. 2000; Lou and Cukier 2006).
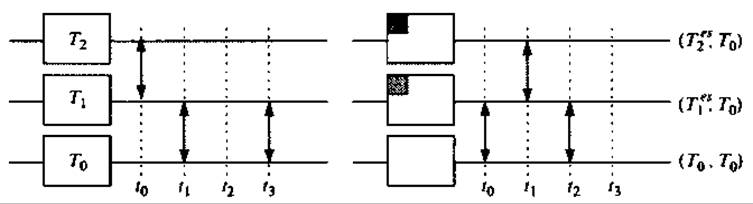
Рис. 9.6. Схематическое сравнение алгоритма REX при стандартной температуре (слева) и алгоритма TEE-REX (справа) для случая расчета с тремя репликами. Температуры расположены по возрастанию, Ті+1 > Т. Попытки обмена (↔) предпринимаются (...) с частотой vex. В отличие от REX, в методе TEE-REX возбуждению подвергается только коллективное подпространство {es} (essential subspace) (серые квадраты), содержащее несколько коллективных мод в каждой реплике. Референсная реплика (Т0, Т0), содержащая приблизительно больцмановский ансамбль, используется для анализа
Для решения задачи выяснения функционирования белка успешно применяется и другой класс методов улучшенного сэмплирования, который выходит за рамки традиционной МД. Эти алгоритмы используют то наблюдение, что флуктуации в белках в общем случае скоррелированы. Выделение таких коллективных мод движения и их применение к новым алгоритмам сэмплирования будет предметом рассмотрения в двух следующих разделах.