Структура и функционирование белков. Применение методов биоинформатики - Джон Ригден 2014
Предсказание структуры белков ab initio
Энергетические функции
Сочетание эмпирических энергетических функций и сборки из фрагментов
В основу эмпирического потенциала положены эмпирические энергетические термы4, которые установлены на основе статистических данных об известных белковых структурах, размещенных в базе данных PDB. Эти энергетические термы, согласно Сколнику (2006), можно разделить на две группы. К первой группе принадлежат общие энергетические члены и энергетические члены, не зависящие от аминокислотной последователь ности, например, вклад водородных связей или жесткость основной цепи пептида (Zhang et al. 2003). Вторая группа содержит энергетические термы, зависящие от аминокислотного состава или последовательности белка, например, потенциал парных взаимодействий остатков (Skolnick et al. 1997), потенциал атомных взаимодействий, зависящих от расстояния (Samudrala and Moult 1998; Lu and Skolnick 2001; Zhou and Zhou 2002; Shen and Sali 2006), член, отражающий предрасположенность к формированию той или иной вторичной структуры (Zhang et al. 2003, 2006; Zhang and Skolnick 2005a).
4 По устоявшейся терминологии, терм - это одно из слагаемых энергетической функции. Прим. перев.
В большинстве эмпирических силовых полей учитывается предрасположенность вторичной структуры, однако локальную структуру белка, вероятно, довольно сложно воспроизвести при упрощенном моделировании. Иными словами, в природе для разнообразных белковых последовательностей характерны, как правило, либо спиральные, либо распрямленные элементы структуры в зависимости от едва уловимых различий в локальном и глобальном окружении последовательностей, однако пока еще не созданы силовые поля, которые могут воспроизводить такие тонкие различия должным образом. Один из способов обойти эту проблему состоит в непосредственном использовании для сборки пространственных моделей фрагментов вторичной структуры, полученных на основе анализа последовательностей или в ходе выравнивания профилей. Дополнительное преимущество такого подхода заключается в том, что использование вырезанных фрагментов вторичной структуры может значительно снизить энтропию при конформационном поиске.
В настоящем разделе представлены два метода предсказания структуры белков, в основу которых положены эмпирические энергетические функции. Показано, что эти методы принадлежат к числу наиболее успешных методов предсказания структуры белков ab initio (Simons et al. 1997; Zhang and Skolnick 2004a).
Одна из наиболее широко известных идей в моделировании ab initio была впервые предложена Боуи и Эйзенбергом. Они создавали белковые модели, собирая небольшие фрагменты (преимущественно нонамеры), взятые из базы данных PDB (Bowie and Eisenberg 1994). Используя аналогичную идею, Бейкер и его коллеги разработали метод ROSETTA (Simons et al. 1997), который оказался весьма успешным при свободном моделировании мишеней в экспериментах CASR. Это привело к тому, что подход, основанный на сборке фрагментов, стал очень популярным в научном сообществе. В последних версиях ROSETTA (Bradley et al. 2005; Das et al. 2007) авторы сначала создавали упрощенные модели, конформации которых были представлены тяжелой основной цепью белка и атомами Cß. На второй стадии ряд отобранных моделей низкого разрешения проходил процедуру уточнения структуры с использованием полноатомной рациональной энергетической функции, которая включала взаимодействия Ван- дер-Ваальса, свободную энергию парных взаимодействий с растворителем и зависящий от ориентации потенциал водородных связей. Блок-схема двухстадийного моделирования представлена на рис. 1.2; подробности описания энергетических функций можно найти в ссылках (Bradley et al. 2005; Das et al. 2007). В ходе конформационного поиска осуществляется большое количество циклов минимизации энергии методом Монте-Карло (Li and Scheraga 1987). Наиболее ярким примером применения этого двухстадийного протокола является слепое предсказание структуры мишени ab initio (Т0281 из CASP6, 70 остатков), для которой СКО атомов Са от кристаллографической структуры составило 1,6 A (Bradley et al. 2005). В CASP7 широкое сэмплирование осуществлялась с помощью распределенных сетевых вычислений Rosetta@home, что давало возможность использовать около 500000 часов процессорного времени для каждого домена мишени. Одна из мишеней, Т0283, была создана в ходе моделирования по шаблону, однако моделирование осуществлялось ROSETTA с использованием протокола ab initio. Полученная таким образом модель имела CKO = 1,8 А для 92 остатков из 112 (рис. 1.3, слева). Несмотря на значительные успехи, описанная процедура является довольно затратной в отношении вычислительных ресурсов, что препятствует ее повседневному использованию.
Заметные успехи алгоритма ROSETTA, а также ограниченная доступность энергетических функций этого метода привели к тому, что некоторые исследовательские группы приступили к самостоятельной разработке энергетических функций, основанных на идее ROSETTA. К числу программ - производных ROSETTA принадлежат Simfold (Fujitsuka et al. 2006) и Profesy (Lee et al. 2004); их энергетические функции содержат следующие термы: потенциал взаимодействий Ван-дер-Ваальса, потенциалы двугранных углов основной цепи белка, потенциал гидрофобных взаимодействий, потенциал водородных связей для основной цепи белка, ротамерный потенциал, терм энергии парных взаимодействий, потенциал парных взаимодействий ß-тяжей и терм, контролирующий радиус компактизации белка. Однако результаты, полученные при предсказании этими методами, были лишь отчасти успешными по сравнению с ROSETTA.
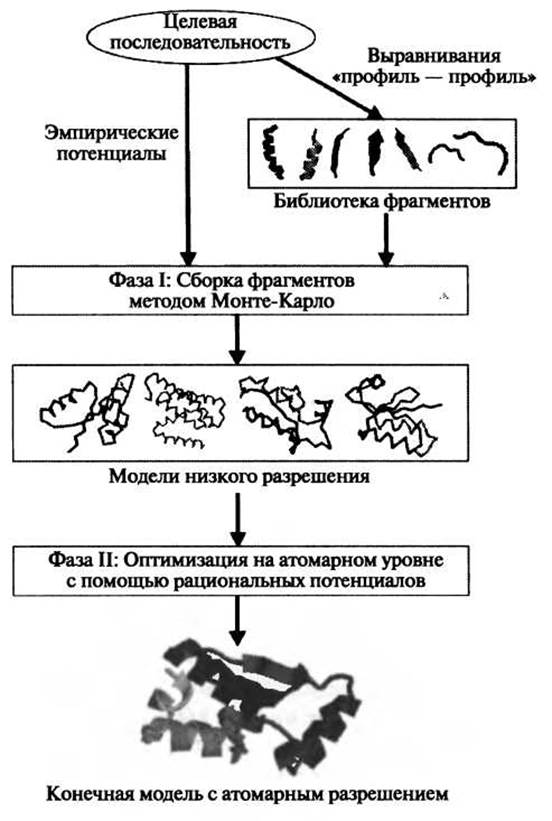
Рис. 1.2. Блок-схема протокола программы ROSETTA
Еще один успешный подход свободного моделирования - это программа TASSER Чжана и Сколника (2004а), которая строит пространственные модели белков исключительно с использованием эмпирических методов. Последовательность мишени сначала “протягивается” через набор репрезентативных белковых структур в процессе поиска возможных
способов укладки. Затем близкие фрагменты (более 5 остатков) извлекают из областей, выровненных в ходе протягивания, и используют при повторной сборке полноразмерных моделей. Области, которые не удалось выровнять, строят с помощью методов моделирования ab initio (Zhang et al. 2003). Конформация белка в TASSER представлена набором Ca-атомов и центрами масс боковых цепей. Процесс повторной сборки осуществляется с помощью параллельного моделирования методом Монте-Карло. Энергетические потенциалы TASSER содержат информацию о предсказанных предрасположенностях вторичной структуры, водородных связях основной цепи, различных коротко- и дальнодействующих корреляциях и энергии гидрофобных взаимодействий, которая основана на статистических данных о структурах из библиотеки PDB. Вклады эмпирических энергетических потенциалов оптимизированы с использованием большого набора структурных макетов (Zhang et al. 2003), что приводит к согласованию сложных взаимосвязей между различными потенциалами взаимодействия.

Рис. 1.3. (Цветную версию рисунка см. на вклейке.) Два примера успешного свободного моделирования из CASP7. Т0283 (слева) - мишень сравнительного моделирования (из Bacillus halodurans) размером 112 остатков. Модель построена с помощью полноатомного метода ROSETTA (гибридный подход, сочетающий в себе физические и эмпирические методы) (Das et al. 2007) на основе свободного моделирования. Оценка (TM-score) составляет 0,74 (Zhang and Skolnick 2004b); значение CKO - 1,8 A для 92 остатков (общее значение CKO - 13,8 Å из-за неправильной ориентации С-концевой спирали). Т0382 (справа) - мишень сравнительного моделирования (из Rhodopseudomonas palustris CGA009) размером 123 остатка. Модель построена с помощью метода I-TASSER (исключительно эмпирический подход) (Zhan 2007). Оценка составляет 0,66; СКО - 3,6 А. Синим и красным цветами показаны модельная и кристаллографическая структуры, соответственно
Существует несколько новых версий TASSER. Одна из них - Chunk-TASSER (Zhou and Skolnick 2007), принадлежащая группе Сколника. Здесь последовательности мишени сначала разделяют на подпоследовательности (“куски”, англ. “chunks”), каждая из которых содержит три последовательных стандартных элемента вторичной структуры (спирали и/или тяжа). Такие подпоследовательности затем сворачиваются независимо. Наконец, на основе моделей подпоследовательностей устанавливаются пространственные ограничения, которые используются для последующего моделирования TASSER.
Еще одна версия - I-TASSER (Wu et al. 2007) - уточняет положение центров масс кластеров TASSER в ходе многократных этапов моделирования методом Монте-Карло. На основании моделей, полученных в первом цикле моделирования TASSER, и структурных шаблонов, определенных с помощью выравнивания в ходе моделирования по шаблону с использованием данных библиотеки PDB, устанавливаются пространственные ограничения, которые затем используются во втором цикле моделирования. Целью моделирования является устранение стерических наталкиваний и уточнение топологии. Блок-схема алгоритма I-TASSER приведена на рис. 1.4. Несмотря на то, что в ходе процедуры используются структурные фрагменты и пространственные ограничения шаблонов, полученных в ходе протягивания, с помощью метода часто удается построить модели, обладающие корректной топологией, даже в тех случаях, когда топологии шаблонов, составляющих модель, некорректны. В CASP7 из 19 мишеней для свободного моделирования и моделирования по шаблону с помощью І-TASSER удалось построить модели с корректной топологией (3-5 А) для 7 последовательностей размером до 155 остатков. На рис. 1.3 (справа) приведен пример Т0382 (123 остатка), для которого начальные шаблоны имели неверную топологию (более 9 Å), однако окончательная модель на 3,6 Å отличалась от структуры, полученной методом рентгеноструктурного анализа. Недавно Хеллесом было проведено сравнительное исследование 18 алгоритмов прогнозирования ab initio. Он пришел к заключению, что I-TASSER - один из лучших методов по таким показателям, как точность моделирования и затраты процессорного времени, приходящиеся на мишень (Helles 2008).
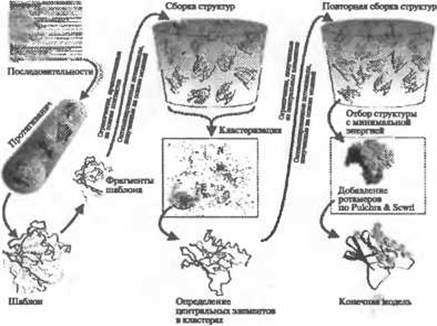
Рис. 1.4. (Цветную версию рисунка см. на вклейке.) Блок-схема программы моделирования структуры белков I-TASSER