БИОЛОГИЯ Том 1 - руководство по общей биологии - 2004

2. РАЗНООБРАЗИЕ ЖИЗНИ НА ЗЕМЛЕ

2.3. Прокариоты

2.3.5. Рост популяции бактерий

2.1. Рассмотрим ситуацию, когда одиночная бактериальная клетка помещена в питательную среду и находится в условиях, оптимальных для роста. Перепишите табл. 2.4 и заполните ее, исходя из предположения, что эта клетка и все ее потомки делятся каждые 20 мин.

На основе данных заполненной вами таблицы постройте графики.

По вертикальной оси отложите число бактерий (кривая А) и десятичный логарифм этого числа (кривая Б), а по горизонтальной оси - время.

Что можно сказать о форме этих кривых?

Когда число клеток увеличивается, как видно из заполненной вами табл. 2.4, говорят о логарифмическом, экспоненциальном или геометрическом росте. В этом случае мы получим экспоненциальный ряд чисел. Это гораздо легче понять, если посмотреть на строку В в табл. 2.4, где число бактерий выражено в виде числа 2, возведенного в соответствующую степень. Показатель степени можно назвать логарифмом или экспонентной числа 2. Логарифмы, или экспоненты, образуют линейный ряд 0, 1, 2, 3 и т. д., соответствующий числу генераций.

Таблица 2.4. Рост модельной популяции бактерий

Вернемся к табл. 2.4; вместо чисел, расположенных в строке А, можно записать их логарифмы по основанию 2 следующим образом:

Сравните строки В и Г. Однако обычно пользуются десятичными логарифмами (см. строку Б). В этом случае 1 = 10⁰, 2 = 10^0,3, 4 = 10^0,6 и т. д.

Кривая, полученная на основе данных строки А (табл. 2.4.), называется логарифмической или экспоненциальной кривой. Такую кривую можно преобразовать в прямую, построив график изменения числа клеток во времени. Тогда в идеальных условиях рост бактерий теоретически должен быть экспоненциальным.

Сравним эту математическую модель с кривой роста реальной популяции бактерий, изображенной на рис. 2.15. Отчетливо видны четыре фазы роста.

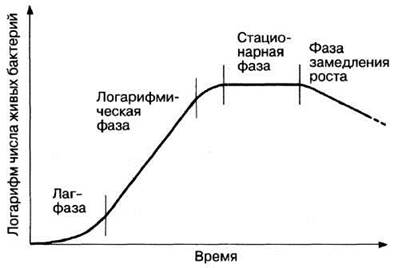
Рис. 2.15. Типичная кривая роста популяции бактерий.

1. Во время лаг-фазы бактерии адаптируются к новой среде обитания, и поэтому рост пока еще не достигает максимальной скорости. В этот период у бактерий могут, например, синтезироваться новые ферменты, необходимые для усвоения тех питательных веществ, которые содержатся в новой среде.

2. Логарифмическая фаза — это фаза, когда бактерии растут с максимальной скоростью, число клеток увеличивается почти экспоненциально, а кривая роста представляет собой практически прямую.

3. В конце концов рост колонии начинает замедляться, и культура входит в стационарную фазу, когда скорость роста равна нулю и когда резко возрастает конкуренция за пищевые ресурсы. Образование новых клеток замедляется, а затем совсем прекращается. Увеличение числа клеток компенсируется одновременной гибелью других клеток, поэтому число жизнеспособных клеток остается постоянным (табл. 2.5). Переход к этой фазе обусловлен действием нескольких факторов: снижением концентрации питательных веществ в среде, накоплением токсичных продуктов метаболизма, а в случае аэробных бактерий и уменьшением содержания кислорода в среде.

4. Во время последней фазы — фазы замедления роста — ускоряется гибель клеток и прекращается их размножение. Способы подсчета клеток описаны в практических занятиях в конце гл. 12.

Таблица 2.5. Культура бактерий при 30 °С