БИОЛОГИЯ Том 2 - руководство по общей биологии - 2004
12. МИКРОБИОЛОГИЯ И БИОТЕХНОЛОГИЯ
12.5. Рост бактерий
12.5.1. Рост популяции
Когда бактериальные клетки достигают определенных размеров, они переходят к бесполому размножению, которое называется простым делением; при этом клетка делится на две идентичные дочерние клетки (рис. 2.11). Детали этого процесса описаны в разд. 2.5.3. В этой главе мы подробно рассмотрим рост целой популяции.
Если одиночную бактерию поместить в питательную среду в оптиматьных условиях роста, то она и ее потомки будут делиться каждые 30 мин, как показано в табл. 12.2.
Таблица 12.2. Рост модельной популяции бактерий
Время, ч |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
5,5 |
4 |
4,5 |
5 |
|
* |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
А |
** |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
Б |
*** |
0,0 |
0,3 |
0,6 |
0,9 |
1,2 |
1,5 |
1,8 |
2,1 |
2,4 |
2,7 |
3,0 |
В |
**** |
2° |
2' |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
210 |
Г |
***** |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
* Число делений ** Число бактерий *** lg числа бактерий **** Число бактерий, выраженное в виде степени числа 2. ***** log2 числа бактерий |
||||||||||||
12.5. Если вы еще не ответили на вопрос 2.1 в гл. 2, то используйте данные из таблицы 12.2 для построения графиков зависимости числа бактерий (график А) и lg числа бактерий (график Б) от времени. Что можно сказать о форме таких графиков?
Увеличение числа клеток, как показано в табл. 12.2, характерно для логарифмического, или экспоненциального, роста. Его легко объяснить, если рассмотреть строку В в табл. 12.2, где число бактерий выражено в виде числа 2, возведенного в определенную степень. Показатель степени можно назвать логарифмом (log), или экспонентой. Логарифмы, или экспоненты, образуют линейно увеличивающийся ряд 0, 1,2, 3, и т. д., соответственно числу делений.
Числа в графе А таблицы 12.2 можно представить в виде логарифмов по основанию 2, как показано в строке Г. (Сравните строку В со строкой Г.) Однако принято использовать логарифмы с основанием 10, как в строке Б. Таким образом, 1 это 100, 2 это 100,3, 4 это 100,6, и т. д.
Кривая на графике А в вопросе 12.5 представляет собой логарифмическую, или экспоненциальную, кривую. Такие кривые роста можно преобразовать в прямые, построив графики в полулогарифмическом масштабе. Таким образом, в идеальных условиях рост бактерий является экспоненциальным. При экспоненциальном росте время, которое требуется для удвоения числа бактерий, постоянно. Оно называется временем удвоения, или временем генерации, и его можно рассчитать, исходя из графика.
Идеальную модель роста популяции бактерий можно сравнить с ростом реальной популяции в закрытом сосуде, где нет внешних воздействий, например не добавляются питательные вещества (рис. 12.8). Заметьте, что приведены две кривые, одна из которых отражает общее число бактерий, включая погибших. На практике легче всего определить именно это число (разд. 12.6.2). Второй график, наиболее интересный для изучения, отражает число жизнеспособных бактерий (разд. 12.6.1). Эта кривая имеет четыре фазы. Первая — это лаг-фаза, в ходе которой бактерии адаптируются к новой среде обитания, и максимальная скорость роста не достигается. В этот период в клетках бактерий могут, например, синтезироваться новые ферменты, необходимые для усвоения тех питательных веществ, которые присутствуют в новой среде.
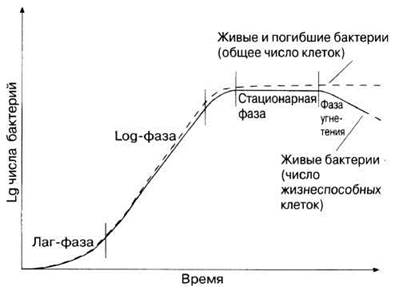
Рис. 12.8. Типичный рост бактериальной популяции.
Следующая фаза — логарифмическая, когда бактерии растут с максимальной скоростью, число бактерий увеличивается почти экспоненциально, т. е. кривая роста представляет собой почти прямую линию. В ходе этой фазы время удвоения остается постоянным и имеет минимальное значение. Со временем рост колонии начинает замедляться, время удвоения начинает увеличиваться, и культура входит в стационарную фазу, когда скорость роста популяции равна нулю и когда резко возрастает конкуренция за пищевые ресурсы. Образование новых клеток замедляется и затем совсем прекращается. Любое увеличение числа клеток компенсируется одновременной гибелью других клеток, поэтому суммарная численность живых клеток остается постоянной. Переход к этой фазе определяется действием ряда факторов: истощением необходимых питательных веществ, накоплением токсичных продуктов распада, таких как спирт, а в случае аэробных бактерий еще и ограничением доступа кислорода. Рост бактерий замедляется также при изменении pH.
Во время последней фазы — фазы замедления роста — возрастает скорость гибели клеток, и она становится выше, чем скорость размножения. Со временем клетки вообще прекращают воспроизводиться. Методы подсчета числа бактерий описаны в следующем разделе.
12.6. Какой вид будет иметь график роста, если пробу бактерий отобрали в начале стационарной фазы роста культуры, засеяли в свежую среду и измеряли рост популяции?
12.7. Культура бактерий была посеяна в питательную среду и выдерживалась при 30 °С. Начиная с точки 0 через определенные интервалы времени, указанные в табл. 12.3, подсчитывали число бактериальных клеток в культуре. Используя данные табл. 12.3, начертите графики роста. Объясните, используя ваши графики, чем вызваны изменения числа клеток.
12.8. Каково минимальное время удвоения (время генерации) бактерий в вопросе 12.7?
Таблица 12.3. Культура бактерий при 30 °С
Время, ч |
Число клеток, млн. |
|
живых |
живых и мертвых |
|
0 |
9 |
10 |
1 |
10 |
11 |
2 |
11 |
12 |
5 |
18 |
20 |
10 |
400 |
450 |
12 |
550 |
620 |
15 |
550 |
700 |
20 |
550 |
850 |
30 |
550 |
950 |
35 |
225 |
950 |
45 |
30 |
950 |
Те же принципы применимы к росту любых популяций, даже популяций человека. Теоретически любая популяция может достичь экспоненциального роста, если время удвоения остается постоянным. Однако рано или поздно в дело вступают лимитирующие факторы, и изучение этих факторов составляет основу популяционной экологии (разд. 10.7).