Фізіологія людини - Вільям Ф. Ґанонґ 2002
Додаток
ГОЛОВНІ ДЖЕРЕЛА
Для вивчення фізіології доцільно користуватися фундаментальними вичерпними підручниками. До найліпших, виданих за останні десять років, належать:
Berne RM, Levy MN (editors): Physiology, 3rd ed. Mosby, 1993.
Guyton AC, Hall JE: Textbook of Medical Physiology, 9th ed. Saunders, 1996.
Johnson LR (editor): Essential Medical Physiology, Raven- Press, 1992.
West JB (editor): Best and Taylor s Physiological Basis of Medical Practice, 12th ed. Williams & Wilkins, 1990.
McPhee, Lingappa, Ganong, and Lange нещодавно опублікували третє видання підручника з патофізіології для студентів, які вивчають клінічну медицину:
McPhee SJ et al: Pathophysiology of Disease: An Introduction to Clinical Medicine, 3rd ed. McGraw-Hill, 2000.
Зазначимо ще такі підручники патофізіології:
Frоhlich ED (editor): Pathophysiology, 3rd ed. Lippincott, 1984.
Sodeman WA Jr, Sodeman WA: Pathologic Physiology, 6th ed. Saunders, 1979.
Класичним підручником з анатомії є:
Bannister LH et al (editors): Grays Anatomy: The Anatomical Basis of Medicine and Surgery, 38th ed. Churchill Livingstone, 1995.
Сучасні візуальні методи досліджень, що стали ключовою частиною сучасної фізіології та медицини, викладені в:
Haaga JR, Alfidi RJ (editors): Computed Tomography of the Whole Body, 2nd ed. Mosby, 1988.
Von Schultress GR: Clinical Positron Emission Tomography. Lippincott Williams & Wilkins, 1999.
Чудові огляди сучасних досліджень у різних ділянках фізіології дібрані у розділах новин, оглядів та перспектив у журналах Nature і Science. Проблемні статті та різні огляди з’являються в New England Journal of Medicine. Це, зокрема, оглядові статті про сучасні дослідження у фізіології та біохімії, які дають найновішу інформацію для лікарів-практиків. Найдоречнішими є серії оглядових публікацій у PhysilogicalReviews, Pharmacilogical Reviews, Annual Reviws of Physiology та в журналах інших серій.
Нещодавно виданий підручник Handbook of Physiology, Oxford University Press, New York складається з окремих томів, які покривають усі розділи фізіології. Розділи є науково цінними, проте надзвичайно деталізовані.
ПОКАЗНИКИ НОРМИ ТА СТАТИСТИЧНЕ ОПРАЦЮВАННЯ ДАНИХ
Межі показників людей у нормі для деяких загально- вимірюваних складників плазми наведені у таблицях, розміщених на внутрішньому боці обкладинки книги. У цілому світі триває спроба перейти до єдиної стандартизованої номенклатури на базі системи СІ. Система побудована на семи незалежних фізичних величинах (див. табл. 1). Похідні одиниці наведені у табл. 2, а префікси, що уживаються - у табл. 3. Трапляються труднощі під час уживання таких одиниць - наприклад, проблема вираження одиниці ензимів - їх мало обговорюють в медичній літературі. У нашій книзі значення величин у тексті наведені в традиційних одиницях, однак у більшості випадків супроводжуються значеннями у системі СІ.
Точність методів, які використовують для лабораторних досліджень, різна. Важливо для оцінки будь-якого окремого вимірювання знати можливі похибки вимірювань. Для хімічного визначення рідин організму вони складаються з похибки, що виникає під час проб, та похибки хімічного методу. Однак, навіть застосовуючи найточніші методи, результати, отримані для різних нормальних осіб, відрізнятимуться внаслідок так званої біологічної варіації. Варіаційність результатів виникає тому, що у будь-якій системі - живому організмі чи тканині - є багато особливостей, які впливають на конкретне вимірювання. Такі показники, як вік, стать, час вимірювань, час після споживання їжі тощо треба брати до уваги.
Показники меж у нормі для будь-якого фізіологічного або клінічного вимірювання можна визначити за допомогою стандартного статистичного аналізу, якщо вимірювання виконано на належній вибірці у нормальній популяції (найліпше понад 20 осіб). Важливо знати не тільки середнє значення для такої вибірки, а й межі розкиду значень осіб від середнього значення.
Таблиця 1. Головні одиниці СІ
Величина |
Назва |
Скорочення |
Довжина |
метр |
м |
Маса |
кілограм |
кг |
Час |
секунда |
с |
Електричний струм |
ампер |
А |
Термодинамічна температура |
кельвін |
К |
Інтенсивність світла |
кандела |
кд |
Кількість речовини |
моль |
моль |
Середнє значення (середнє арифметичне, М) показників обчислюють за формулою
![]()
де X - окремі заначення; n - кількість окремих показників у серії.
Середнє відхилення - це середнє значення відхилень кожного з показників від середнього арифметичного значення. З математичного погляду найліпше визначити відхилення за допомогою середнього геометричного значення відхилень від М, що називають стандартним відхиленням вибірки (s):
![]()
З математичних міркувань використовують n-1, а не n. Значення s може відрізнятися від стандартного відхилення середнього значення для всієї популяції, яке позначають σ. Однак якщо вибірка є справді репрезентативною, то s і σ будуть сумірними.
Іншим уживаним показником розкиду значень є стандартна похибка середнього значення (СПСЗ):
![]()
СПСЗ відображає надійність середнього значення вибірки як представника справжнього середнього значення для загальної популяції, від якої вибірка була зроблена.
Крива частотного розподілу може бути побудована з окремих значень популяції з нанесенням частоти, з якою будь-яке окреме значення трапляється у серії стосовно інших значень. Якщо група осіб, яку тестують, гомогенна, то крива розподілу є симетричною (рис. 1) з найбільшою частотою для середнього значення і ширина кривої залежить від а (крива нормального розподілу). В межах ідеальної кривої нормального розподілу відсоток спостережень, що належать до різних меж, наведений у табл. 4. Середнє значення і s у репрезентативній вибірці наближаються до середнього значення і а цілої популяції. Тому можна передбачити на підставі середнього значення і s вибірки ймовірність того, що будь-яке окреме значення у загальній популяції є нормальним. Наприклад, якщо розкид між таким значенням і середнім дорівнює 1,96s, то ймовірність того, що воно є нормальним становить 1 з 20 (5 зі 100). Звичайно, ймовірність того, що значення є анормальним, становить 19 з 20.
Таблиця 2. Похідні одиниці СІ
Величина |
Назва одиниці |
Скорочення |
Площа |
квадратний метр |
м2 |
Кліренс Концентрація |
літр/секунда |
л/с |
Маси |
кілограм/літр |
кг/л |
Речовини |
моль/літр |
моль/л |
Густина |
кілограм/літр |
кг/л |
Електричний потенціал |
вольт |
В |
Енергія |
джоуль |
Дж |
Сила |
ньютон |
Н |
Частота |
герц |
Гц |
Тиск |
паскаль |
Па |
Температура |
градус Цельсія |
°С |
Об’єм |
кубічний метр |
м3 |
літр |
Л |
Статистичний аналіз використовують також для визначення різниці між двома середніми значеннями. У фізіологічних та клінічних дослідженнях вимірювання часто виконують на групі тварин чи хворих, які отримують лікування. Такі вимірювання порівнюють з такими ж вимірюваннями, зробленими на контрольній групі, що ідеально була піддана тотожному впливу, і має однакові стани, окрім того, що лікування не проводилось. Якщо середнє значення для групи, що отримувала лікування відрізняється від відповідного середнього значення для контрольної групи, то постає питання, чи отримана різниця є наслідком лікування чи розкиду значень. Ймовірність того, що різниця репрезентує розкид значень, можна визначити у багатьох випадках за допомогою показника Стюдента t. Показник t є відношенням різниці між середніми значеннями
Таблиця 3. Стандартні префікси1
Префікс |
Абревіатура |
Значення |
екса- |
Е |
1018 |
пета- |
П |
1015 |
тера- |
Т |
1012 |
гіга- |
г |
109 |
мега- |
м |
106 |
кіло- |
к |
103 |
гекто- |
г |
102 |
дека- |
да |
101 |
деци- |
деци |
10-1 |
санти- |
санти |
10-2 |
мілі- |
мл |
10-3 |
мікро- |
мк |
10-6 |
нано- |
н |
10-9 |
піко- |
пк |
10-12 |
фемто- |
Ф |
10-15 |
атто- |
а |
10-18 |
1 Такі префікси використовують для одиниць СІ та інших. Наприклад, мікрометр (мкм) - це 10-6 метра (також називають мікрон); піколітр (пл) - 10-12 літра; кілограм (кг) - 103 грама
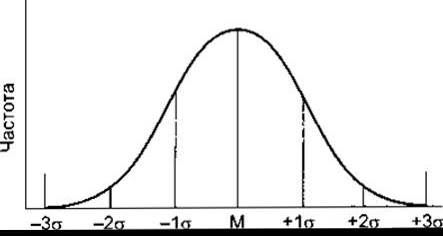
Рис. 1. Крива нормального розподілу (крива частотного розподілу значень для гомогенної популяції).
двох серій (Ма і Мb) і похибки цих середніх. Формула, яку використовують для розрахунків, має вигляд
![]()
де na і nb - кількість окремих показників у серіях а і b, відповідно. Якщо na = nb, то формула для визначення t стає простішою:
![]()
Чим більше значення t, тим менша ймовірність, що різниця репрезентує розкид значень. Ця ймовірність зменшується, якщо кількість осіб n у кожній групі зростає, оскільки чим більша кількість вимірювань, тим менша похибка вимірювань. Математичний вираз ймовірності Р для будь-якого значення t за різних значень n можна відшукати у таблицях, наведених у більшості книжок зі статистики. Величина Р - це дробове число, яке відображає ймовірність того, що різниця між двома середніми значеннями є наслідком розкиду значень. Наприклад, якщо Р дорівнює 0,10, то ймовірність того, що різниця є наслідком розкиду значень, становить 10% (1 шанс на 10). Показник Р < 0,001 свідчить, що ймовірність того, що різниця виникла внаслідок розкиду значень, є меншою, ніж 1 до 1000. Якщо Р < 0,05, то більшість дослідників називають різницю «статистично достовірною»; тобто уважають, що різниця є наслідком дії певного чинника, а не випадковістю. Використання t-тесту має сенс лише для порівняння двох груп. У випадку експериментів, що налічують більше двох груп, з’явиться систематична похибка, яка спричинить завищене значення ймовірності. У таких випадках застосовують дисперсійний аналіз. Ця та інші методики описані у книгах зі статистики.
Таблиця 4. Відсоток значень популяції, які відповідають різним межам для кривої нормального розподілу
Середнє значення ± s |
68,27% |
Середнє значення ± 1,96 s |
95,00% |
Середнє значення ± 2 s |
95,45% |
Середнє значення ± 3 s |
99,73% |
Згадані елементарні методи та багато інших, придатних для статистичного аналізу в дослідних лабораторіях та клініках, забезпечують визначення об’єктивних середніх значень. Статистична значимість не є свавільною для середнього фізіологічного значення і протилежне є інколи правильним; проте заміна суб’єктивних вражень результатами статистичного аналізу є важливою метою у медицині.
До корисних книг зі статистики належать:
Dawson-Saunders В, TrappRG: Basic and Clinical Biostatistics, 2nd ed. Appleton & Lange, 1994.
Rosner B: Fundamentals of Biostatistics. Duxbury, 1982.
The SI for the Health Professions: World Health Organization, 1977.
Zar JH: Biostatistical Analysis. Prentice-Hall, 1974.
Стандартні респіраторні позначення
(див. Handbook of Physiology, Section 3: The Respiratory System. American Physiological Society, 1986)
Головні змінні |
А |
Альвеолярний газ |
|
V |
Об’єм газу |
Д |
Дихальний газ |
V |
Об’єм газу/одиницю часу. (Крапка зверху - позначка, |
М |
Газ мертвого простору |
що означає швидкість) |
В |
Барометричний |
|
р |
Тиск газу |
а |
Артеріальна кров |
р |
Середній тиск газу |
к |
Капілярна кров |
ЧДР |
Частота дихання (кількість дихальних рухів/одиницю часу) |
в |
Венозна кров |
D |
Дифузійна ємність |
Молекулярні різновиди |
|
F |
Фракційна концентрація у фазі сухого газу |
Позначають хімічними формулами, надрукованими у індексі |
|
R Q |
Співвідношення респіраторного газообміну= VCО2/VО2 Об’єм крові Локалізація (букви для нижніх індексів) |
Приклади |
|
І |
Інспіраторний газ |
РІО2 |
- Тиск кисню у інспіраторному газі |
Е |
Експіраторний газ |
VM |
- Об’єм газу у мервому просторі |
Еквіваленти метричних, американських та англійських вимірювань
(значення заокруглені до двох цифр після десяткової коми)
Довжина
1 кілометр = 0,62 милі
1 миля = 5280 футів = 1,62 кілометри
1 метр = 39,37 дюймів
1 дюйм = 1/12 фута =2,54 сантиметра
Об’єм
1 літр = 1,06 американської кварти
1 американська кварта = 32 унції = 1/4 американського галону = 0,95 літра
1 мілілітр = 0,03 унції
1 унція = 29, 57 мілілітрів
1 американський галон = 0,83 англійського галону
Маса
1 кілограм = 2,2 фунта (британського) = 2,68 фунта (аптекарського)
1 фунт (британський) = 16 унцій = 453,60 грама
1 гран = 65 міліграма Енергія
1 кілограм-метр = 7,25 футів-фунтів
1 фут-фунт = 0,14 кілограм-метрів
Температура
Для перетворення градусів Цельсія у градуси Фаренгейта помножте на 9/5 і додайте 32
Для перетворення градусів Фаренгейта у градуси Цельсія віднімінь 32 і помножте на 5/9
Грецький алфавіт
Символ |
Назва |
Символ |
Назва |
||
А |
а |
Альфа |
N |
ν |
Ню |
В |
β |
Бета |
Е |
ξ |
Ксі |
Г |
y |
Гамма |
О |
o |
Омікрон |
Δ |
δ |
Дельта |
П |
п |
Пі |
Е |
ε |
Епсилон |
Р |
р |
Ро |
Z |
ζ |
Зета |
І |
σ,ς |
Сигма |
H |
η |
Ета |
Т |
т |
Тау |
Θ |
θ,ϑ |
Тета |
Y |
ν |
Іпсілон |
І |
ι |
Йота |
Ф |
ϕ,φ |
Фі |
Κ |
κ |
Каппа |
X |
χ |
Хі |
Λ |
λ |
Ламбда |
ψ |
ψ |
Псі |
М |
μ |
Мю |
Ω |
ω |
Омега |