Основы биоинформатики - Огурцов А.Н. 2013
Методы биоинформационного анализа
Алгоритмы выравнивания последовательностей
Значимость выравниваний
Для оценки биологической значимости выравнивания данной последовательности с другими последовательностями из баз данных принято сравнивать полученные результаты с результатами выравнивания данной последовательности с последовательностями, полученными с помощью статистически случайных перестановок элементов (рандомизации) в последовательностях из баз данных.
Очевидно, что если рандомизированные (случайные) последовательности дают такой же результат, как и исходные, то, скорее всего, выравнивание не имеет биологического смысла.
Для оценки значимости выравниваний обычно используют такие статистические параметры, как Z-score, P-value и E-value.
Z-score показывает, насколько необычно обнаруженное нами совпадение, то есть в терминах статистики — это расстояние (измеряемое как среднеквадратическое отклонение) данного уровня от среднего значения по набору данных. Если вес исходного выравнивания данной последовательности с другой последовательностью равен S, то
![]()
где μ - среднее значение выравниваний данной последовательности с рандомизированными вариантами второй последовательности; а - стандартное отклонение.
При Z = 0 для двух белковых последовательностей - эти белки похожи друг на друга, не сильней, чем (в среднем) на белки из некоторой контрольной группы, по которой и производится сравнение, что, впрочем, вполне может произойти случайно. Чем больше Z-score, тем больше вероятность того, что наблюдаемое выравнивание появилось неслучайно. Опыт показывает, что Z-score > 5 уже говорит о значимости исходного выравнивания.
P-value. Многие программы выдают величины Р (Р-value) - вероятности того, что выравнивание не лучше, чем случайное. Связь Z-score и Р зависит от распределения весов контрольных выравниваний, которое не соответствует нормальному распределению.
Ориентировочно значения P-value можно интерпретировать следующим образом:
|
P ≤ 10-100 |
точное совпадение; |
|
10-100 < Р < 10-50 |
последовательности почти идентичны, например, аллели или полиморфизмы; |
|
10-50 < Р < 10-10 |
близкородственные последовательности; гомология очевидна; |
|
10-10 < Р < 10-1 |
обычно дальнеродственные последовательности; |
|
Р > 10-1 |
по-видимому, соответствие незначимо. |
E-value. Программы поиска по базам данных, в том числе и PSI- BLAST, указывают E-value.
E-value выравнивания - это ожидаемое количество последовательностей, которые бы имели Z-score такой же (или лучше), как если бы мы в качестве запроса дали программе случайную последовательность.
Ориентировочно значения E-value можно интерпретировать следующим образом:
|
Е < 0,02 |
вероятно, последовательности являются гомологами; |
|
0,02 < Е < 1 |
гомология не очевидна; |
|
Е > 1 |
следует ожидать, что это случайное совпадение. |
Следует отметить, что статистические оценки полезны и необходимы, но они не могут заменить здравый смысл и тщательный и аккуратный анализ биологичности результатов.
Существует множество эмпирических правил интерпретации процента идентичных аминокислотных остатков в оптимальном выравнивании белковых последовательностей.
Если два белка содержат более 45% идентичных остатков в их оптимальном выравнивании, то есть все основания предполагать, что эти белки имеют подобные структуры и, скорее всего, общую или, по крайней мере, сходную функцию.
Если они содержат более 25% идентичных остатков, они, вероятно, имеют подобный фолдинг.
С другой стороны, низкая степень сходства последовательностей не может исключить возможность гомологии.
Рассел Дулитл (Russell F. Doolittle) определил область 18-25% сходства последовательностей как область двусмысленности (или, область неоднозначности), для которой предположение о гомологии можно высказывать только в качестве гипотезы. Парные выравнивания, которые находятся ниже этой области, малоинформативны.
При этом отсутствие значимого сходства последовательностей совсем не означает отсутствие сходства структур.
Например, аминокислотные последовательности гомологичных белковых ДНК-захватов (DNA sliding clamps) дрожжей (белок lplq) и Е. coli (белок 2ро1) подобны только на 12%, но они практически одинаковы по структуре и функциям (рисунок 58).
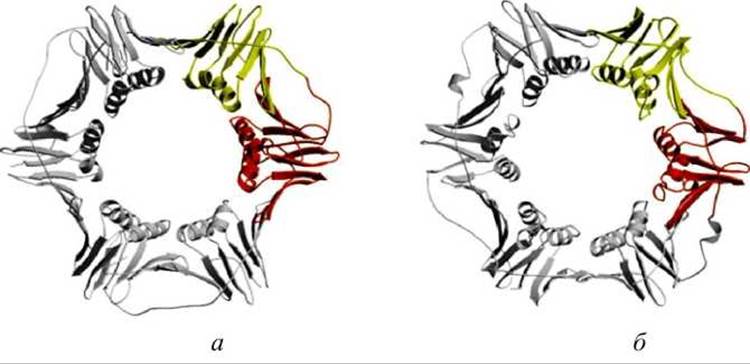
Рисунок 58 - Белки ДНК-захваты: а - дрожжевой белок lplq; б - белок 2ро1 Escherichia coli
Хотя область неоднозначности и ненадежна для выводов, но для решения вопроса об истинном родстве важна также "текстура" (профили) выравнивания - изолированы ли эти сходные остатки и распределены по всей последовательности или же они образуют "айсберги" - локальные участки высокого сходства (ещё один термин Дулитла), которые могут соответствовать общему активному центру. Также полезно использовать дополнительную информацию об общих лигандах или функциях. В случае если пространственные структуры известны, то мы можем проверить их сходство непосредственно.
Эмпирические правила являются скорее рекомендациями, чем закономерностями. Приведём ещё несколько характерных примеров.
Миоглобин кашалота и леггемоглобин люпина имеют 15% идентичных остатков в оптимальном выравнивании. Это также ниже определённой Дулитлом области неоднозначности. Однако известно, что обе молекулы имеют сходные трехмерные структуры, содержат гемовые простетические группы и связывают кислород. Они действительно являются удалёнными гомологами.
Последовательности N- и С-концевых частей в одном и том же белке роданез имеют 11% идентичных остатков в оптимальном выравнивании. Если бы они возникли в разных белках, нельзя было бы судить об их родстве, исходя лишь из последовательностей. Однако такая ситуация в одном белке дает основание полагать, что они произошли путём дупликации и дивергенции генов. Очевидное сходство их структур подтверждает их родство.
Две протеазы химотрипсин и субтилизин имеют последовательности схожие на 12%. Эти сериновые протеазы выполняют сходную функцию и их активный центр образован тремя характерными для них остатками. Тем не менее, они имеют разную пространственную укладку и не родственны (рисунок 59).
Схожесть их каталитических функций - это пример конвергентной эволюции. Поэтому не стоит предполагать родственную связь между белками с непохожими последовательностями, основываясь только на схожести их функций.
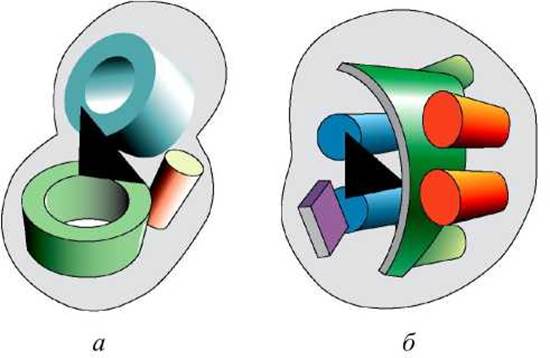
Рисунок 59 - Схема строения сериновых протеаз: а - типа трипсина; б - типа субтилизина. Схематически изображены а-спирали, ß-листы и ß-цилиндры. Район активного центра показан чёрным треугольником
Контрольные вопросы и задания
1. Каковы недостатки метода динамического программирования?
2. За счёт чего сокращается время расчётов в методе динамического программирования?
3. Чем отличаются методы Нидлмена-Вунша и Смита-Уотермана?
4. Каков алгоритм заполнения ячеек F(i,j) матрицы динамического программирования?
5. Используя матрицу замен аминокислот BLOSUM62 и фиксированный штраф за пропуски d = 8, методом Нидлмена-Вунша построить глобальное выравнивание двух фрагментов (и вычислить его счёт (вес))
![]()
6. Какие существуют два отличия алгоритма локального выравнивания от алгоритма глобального выравнивания?
7. Что такое k-кортеж?
8. Какие три статистических параметра используют для оценки значимости выравнивания?