Ускорение - Кинематика

Цели: познакомить учащихся с понятием ускорения - важнейшей характеристикой равноускоренного движения.

Демонстрации: движение тележки с капельницей по наклонной плоскости.

Ход урока

I. Повторение. Проверка домашнего задания

При проверке домашнего задания основное внимание следует уделить четкому усвоению основных определений и положений механики.

Можно провести краткий фронтальный опрос по изученному материалу:

- Что изучает механика? Из каких разделов она состоит?

- Что изучает кинематика?

- Что такое материальная точка? Что такое траектория?

- Что такое механическое движение?

- Как найти путь в прямолинейном равномерном движении?

- Что такое система отсчета?

- При наличии скольких тел можно говорить о механическом движении?

Можно предложить одну-две задачи на более глубокое понимание изученных терминов, например:

а) Во время равномерного движения поезда с верхней полки падает мяч. Будет ли он падать вертикально? Одинаково ли ответят на этот вопрос наблюдатели, находящиеся в вагоне и на платформе?

б) Траектории движения двух материальных точек пересекаются. Означает ли это, что тела сталкиваются? Приведите пример, подтверждающий ваш ответ.

в) Как должен прыгнуть наездник, скачущий на лошади по прямой с постоянной скоростью, чтобы, проскочив сквозь обруч, снова встать на лошадь? Сопротивлением воздуха можно пренебречь.

II. Изучение нового материала

План изложения нового материала:

1. Понятие ускорения.

2. Вывод формулы для ускорения при равноускоренном движении.

3. Графическое описание движения.

1. Переходя к изучению основного материала, следует обратить внимание учащихся на то, что прямолинейное равномерное движение встречается в жизни достаточно редко. Обычно в своем движении тела движутся, меняя свою скорость.

На примере опыта с тележкой учитель показывает, как изменяется скорость тела. Во время демонстрации опыта учитель обращает внимание на то, что с увеличением угла наклона доски скорость тележки изменяется по-разному. При большем угле наклона расстояния между каплями на соответствующих отрезках становятся больше.

Для угла наклона α = 10° имеем (рис. 78):

А для α = 25° получаем (рис. 79):

Такой тип движения, когда скорость тела за равные промежутки времени изменяется на одинаковую величину, называется равноускоренным.

Основной характеристикой такого движения является ускорение (а).

В системе СИ за единицу ускорения принято:

а = [м/с²].

Если, скажем, ускорение тела а = 2 м/с², то это значит, что за 1 секунду скорость тела изменяется на 2 м/с.

Проще говоря, ускорение характеризует быстроту изменения скорости. Диапазон возможных ускорений для различных тел легко проиллюстрировать на примере таблицы № 1 учебника (с. 8).

2. Ускорение, как любая физическая величина, должно быть измерено. Если тело начинает движение из состояния покоя равноускоренно и за время 4 с достигает скорости v = 16 м/с, то ускорение можно найти так:

Если тело движется равнозамедленно, и скорость перед началом торможения равна v₀, то ускорение можно найти так:

Будет полезным, если учащиеся усвоят более общую форму определения ускорения. Если тело уже имеет начальную скорость v₀ и начинает равноускоренно, то через время t оно достигнет скорости:

Откуда:

Именно эта формула является основной в определении ускорения.

Необходимо отметить, что ускорение - векторная величина. Кроме численного значения она имеет направление. При равноускоренном движении ускорение совпадает по направлению со скоростью, при равнозамедленном - направлена в противоположную скорости тела сторону.

3. Далее следует рассмотреть возможность графического построения зависимости скорости тела от времени. Важно понять, что наличие графика скорости дает достаточно полную характеристику движения.

Например (см. рис. 80).

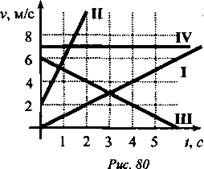
Тело I начинает двигаться равноускоренно из состояния покоя с ускорением а = 1 м/с².

Тело III, имея v₀ = 6 м/с, начинает двигаться равнозамедленно с ускорением по модулю а = 1 м/с². И так далее.

III. Повторение изученного

С целью закрепления понятия ускорения в конце урока можно предложить для коллективного обсуждения ряд качественных задач, например:

1. Поезд начинает тормозить. Как направлено его ускорение? Скорость?

2. Ускорение тела равно -2 м/с². Как это понимать?

3. За 3 с скорость шарика возросла с 2 м/с до 5 м/с. Определите ускорение шарика.

Домашнее задание

1. § 2 учебника; вопросы и задания к параграфу; экспериментальное задание к параграфу (движение монеты по наклонной плоскости).

2. Задачи и упражнения (учебник, с. 126) № 10-14.

Дополнительный материал

Принцип относительности Галилея

Помимо пространственно-временной законы природы обладают еще другой симметрией. Одним из тех, кто первым обратил на нее серьезное внимание, был Галилео Галилей. «Уединитесь, - писал он, - с кем-либо из друзей в просторное помещение под палубой какого-либо корабля, запаситесь мухами, бабочками и другими подобными мелкими летающими насекомыми. Пусть будет у вас там также большой сосуд с водой и плавающими в нем маленькими рыбками. Подвесьте наверху ведерко, из которого вода будет падать капля за каплей в другой сосуд с узким горлышком, подставленный внизу. Пока корабль стоит неподвижно, наблюдайте прилежно, как мелкие летающие животные с одной и той же скоростью движутся во все стороны помещения; рыбы, как вы увидите, будут плавать безразлично во всех направлениях; все падающие капли попадут в подставленный сосуд, и вам, бросая какой-нибудь предмет, не придется бросать его с большей силой в одну сторону, чем в другую, если расстояния будут одни и те же... Прилежно наблюдайте все это, хотя у нас не возникает никакого сомнения в том, что пока корабль стоит неподвижно, все должно происходить именно так. Заставьте теперь корабль двигаться с любой скоростью, и тогда (если только движение будет равномерным и без качки в ту или другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно».

В частности, утверждает Галилей, если с высокой мачты сбросить камень, то он «всегда упадет в одно и то же место корабля, неподвижен ли тот или движется с какой угодно скоростью». Это утверждение многим современникам Галилея показалось сомнительным: тогда была распространена точка зрения, согласно которой чем быстрее движется корабль, тем дальше от подножия мачты должен упасть камень. Нужен был эксперимент, чтобы установить истину. Однако Галилей заявил, что он и без опыта уверен: результат будет таким, как он говорит, ибо «необходимо, чтобы он последовал».

Прошло девять лет, прежде чем был поставлен соответствующий опыт. В 1641 г. вблизи Марселя французский физик Пьер Гассенди в присутствии большого числа свидетелей, находясь на галере, несколько раз (при разных скоростях движения судна) бросил камень с мачты. Однако даже при наибольшей возможной скорости, которую могли обеспечить гребцы, «камень все же падал во всех случаях вдоль мачты к ее подножию, и с той же стороны». После этого все сомнения в справедливости утверждений Галилея отпали.

Итак, одинаково поставленные механические опыты и в системе отсчета, неподвижной относительно Земли, и в тех, что движутся относительно нее равномерно и прямолинейно, приводят к совершенно одинаковым результатам. Эти системы отсчета оказываются физически равноправными - среди них нет никакой преимущественной, как-то выделенной по сравнению с другими системы.

Таким образом, если имеется система отсчета, которую с известной точностью можно считать инерциальной, то с той же самой точностью будут инерциальными и все остальные системы отсчета, движущиеся относительно нее равномерно и прямолинейно.

Позднее закономерность, описанную Галилеем, стали рассматривать в качестве одного из основных принципов механики, для которого впоследствии было предложено название «принцип относительности Галилея».

Одна из первых его формулировок, предложенная Исааком Ньютоном в 1687 г., звучала так: «Относительные движения друг по отношению к другу тел, заключенных в каком-либо пространстве, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно без вращения».

В настоящее время принцип относительности Галилея формулируют следующим образом: законы механики во всех инерциальных системах отсчета имеют один и тот же вид. Именно поэтому, в частности, находясь в закрытом вагоне и проводя в нем различные механические эксперименты, невозможно по их результатам определить, покоится ли этот вагон или движется относительно Земли равномерно и прямолинейно.

Стоит, однако, вагону изменить свою скорость, например, резко затормозить (и тем самым превратиться в инерциальную систему), как падающие с полок вещи сразу дадут понять, движется он или нет.

Во времена Галилея практически вся физика сводилась к механике. Отсюда и «механический» характер принципа относительности Галилея. Но было и другое обстоятельство. В XIX столетии физики считали, что электромагнитные процессы нe подчиняются принципу относительности. В результате получалось, будто этот принцип справедлив для одних явлений природы и несправедлив для других.

Однако в начале XX в. Жюль Анри Пуанкаре и Альберт Эйнштейн сняли имеющиеся несообразности, распространив принцип относительности на все явления природы (при этом, однако, пришлось радикально пересмотреть привычные представления о пространстве и времени). Оказалось, что не только законы механики, но и все другие законы физики во всех инерциальных системах отсчета имеют один и тот же вид.

В современной физике принцип относительности часто формулируют как принцип симметрии: уравнения, выражающие физические законы, должны иметь такой вид, который не меняется при переходе от одной инерциальной системы отсчета к другой. В подобной форме он используется на «переднем крае» физики, при подстроении новых научных теорий. Требуя от уравнений определенной симметрии, такой принцип позволяет установить один из основных критериев для выбора вербного закона из множества различных математических выражений, получаемых учеными в результате тех или иных теоретических построений.

Проиллюстрируем это простым примером. Пусть имеется система из двух частиц, одна из которых (А) действует на другую (В) с силой . По Ньютону, такая сила связана с ускорением частицы В:

А согласно воззрениям, высказывавшимся еще Аристотелем, она должна определять не ускорение, а скорость этой частицы:

где k - некий постоянный (для данного тела) коэффициент пропорциональности.

Какому из уравнений следует отдать предпочтение с точки зрения принципа относительности? Для того чтобы выяснить это, перейдем в другую инерциальную систему отсчета и посмотрим, что произойдет с каждым из уравнений.

Поскольку масса, ускорение и сила во всех инерциальных системах отсчета имеют одинаковые значения, а скорость - разные, нетрудно сообразить, что ньютоновский закон в данном случае сохранит свой вид, а аристотелевский - нет (в нем левая часть останется без изменения, а правая изменится).

Таким образом, из предлагаемых уравнений лишь закон Ньютона, обладая должной симметрией, удовлетворяет требованию принципа относительности, и потому только он может претендовать на роль основного закона механики.