Первый закон Ньютона - Динамика

Цели: знакомство с новым разделом механики — динамикой; изучение содержания Первого закона Ньютона.

Демонстрации: движение шара по гладкой горизонтальной опоре; взаимодействие тел с опорами и подвесами.

Ход урока

I. Анализ итогов тестирования н самостоятельной работы

Перед началом изучения нового материала следует коротко подвести итоги уже изученного материала. Остановившись на контрольной работе, можно проанализировать наиболее типичные ошибки, а также выяснить причины их возникновения.

Далее можно остановиться на кроссворде учебника (с. 18). Обычно ученики успешно справляются с подобными заданиями.

II. Изучение нового материала

План изложения нового материала:

1. Динамика как раздел механики.

2. Демонстрация опытов по взаимодействию тел.

3. Первый закон Ньютона.

4. Область применения законов Ньютона.

5. Доклад о роли И. Ньютона в развитии механики.

1. Прежде всего важно подчеркнуть, что новый раздел механики - динамика - есть логическое продолжение кинематики. Динамика как наука была сформирована и построена в рамках классической физики великим английским ученым И. Ньютоном. При этом Ньютон явился последователем таких ученых, как Галилео Галилей, Коперник и других, которые построили основы науки, развитые и систематизированные Ньютоном.

2. Далее учитель задает вопрос классу:

- Что же изучает динамика, кто может сформулировать? (Ответы учащихся.)

Динамика изучает причины, которыми обусловлено движение.

Учитель демонстрирует различные виды движения тел: движение шара по гладкой опоре (горизонтальной и наклонной); столкновение шаров; движение тела на подвесе и так далее.

Ранее, в 7-ом классе, было сказано, что мерой взаимодействия тел являются возникающие при этом силы. Так как абсолютно изолированных тел в природе нет, то в природе всегда можно обнаружить различные силы.

- Какие силы действуют на тела в показанных опытах? (Ответы учеников.)

- Как двигаются тела под действием названных сил?

На примере движения шара по гладкой поверхности стола (рис. 94) можно заметить, что его скорость заметно не меняется. При этом на шар действуют две заметные по величине вертикальные силы: сила тяжести mg и сила реакции опоры (N), а также одна малозаметная по величине горизонтальная сила - сила трения.

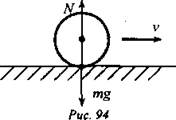
Две вертикальные силы - mg и N себя уравновешивают. Говорят, что эти силы компенсированы. Так как сила трения мала, то скорость шара практически не меняется.

Если бы сила трения строго равнялась нулю, шар сколь угодно двигался бы прямолинейно и равномерно.

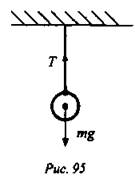
Другой пример. Рассмотрим шарик, который висит на жесткой нити (рис. 95). На него действуют две вертикальные силы: сила тяжести mg и сила натяжения Т. Силы mg и Т компенсированы, в результате чего шар по отношению к опоре неподвижен. В противном случае шар бы перемещался по направлению действия большей силы.

3. В результате многолетних исследований И. Ньютон создал фундаментальный руд «Математические начала натуральной философии». Эта книга и определила основные понятия механики: масса, сила, ускорение. Наиболее важным содержанием труда явились аксиомы, или законы движения. Эти формулировки получили названия законов Ньютона.

Первый закон механики Ньютон сформулировал в виде:

Любое тело, до тех пор пока оно остается изолированным, сохраняет свое состояние покоя или равномерного прямолинейного движения.

Под изолированным телом понимают любую материальную точку, бесконечно удаленную от других материальных объектов.

Важно понять, что в природе нет абсолютно изолированных тел. Мы всегда упрощаем рассматриваемый процесс. В то же время, если силы, действующие на тело, скомпенсированы, результирующая сила равна нулю, и движение тела описывается первым законом Ньютона. В этом случае тело либо покоится, либо двигается прямолинейно и равномерно.

4. Особенным для законов Ньютону, в том числе и для первого, является то, что они выполняются не во всех системах отсчета, а лишь в одном виде Систем отсчета, которые называются инерциальными.

Если связать систему координат с Солнцем, а оси выставить на удаленные звезды, то такая система будет инерциальной, и скорость изолированного тела относительно осей такой системы будет постоянной.

Если систему отсчета построить, связав начало координат с Землей, то она, строго говоря, инерциальной не будет из-за вращения Земли относительно своей оси. Но так как скорость вращения Земли относительно своей оси мала, то во многих случаях такую систему отсчета также можно назвать инерциальной: в рамках физики малых скоростей погрешности такой системы отсчета малозаметны, и ими можно пренебречь.

5. Далее можно заслушать доклад одного из учеников о жизни И. Ньютона и его роли в развитии физики.

III. Закрепление изученного

С целью закрепления материала можно предложить ряд качественных задач по изученной теме, например:

1. Может ли шайба, брошенная хоккеистом, двигаться равномерно по льду?

2. Назовите тела, действие которых компенсируется в следующих случаях: а) айсберг плывет в океане; б) камень лежит на дне ручья; в) подводная лодка равномерно и прямолинейно дрейфует в толще воды; г) аэростат удерживается у земли канатами.

3. При каком условии пароход, плывущий против течения, будет иметь постоянную скорость?

Можно предложить и ряд чуть более сложных задач на понятие инерциальной системы отсчета:

1. Система отсчета жестко связана с лифтом. В каких из приведенных ниже случаев систему отсчета можно считать инерциальной? Лифт: а) свободно падает; б) движется равномерно вверх; в) движется ускоренно вверх; г) движется замедленно вверх; д) движется равномерно вниз.

2. Может ли тело в одно и то же время в одной системе отсчета сохранять свою скорость, а в другой - изменять? Приведите примеры, подтверждающие ваш ответ.

3. Строго говоря, связанная с Землей система отсчета не является инерциальной. Обусловлено ли это: а) тяготением Земли; б) вращением Земли вокруг своей оси; в) движением Земли вокруг Солнца?

Домашнее задание

1. § 7 учебника; вопросы и задания к параграфу.

2. Задачи и упражнения (учебник, с. 126) № 37-40.

3. Сборник задач В. И. Лукашика, Е. В. Ивановой, № 195, 196, 197.