Практическая химия белка - А. Дарбре 1989
Предсказание конформации пептидов и белков
Традиционные методы
Любому научному прогрессу всегда сопутствует противостояние позиций экспериментаторов, осторожно относящихся к новым концепциям, и теоретиков, которые устоявшиеся представления почти всегда рассматривают как приближенные и ограниченные. В настоящем разделе в самом общем виде излагаются некоторые предсказательные приемы, которые экспериментаторы считают достаточно хорошими и охотно используют в своих работах. А затем уже обсуждаются некоторые теоретические возражения против применения этих приемов, а также дается описание улучшенных методов.
Согласно модели твердых сфер, атомы представляют собой шары, размер которых определяется вандерваальсовыми радиусами. Допустимыми считаются конформации, в которых атомы не перекрываются. Если это условие не выполняется хотя бы для одной пары атомов, то такая конформация отвергается. Метод имеет ограниченное применение, поскольку допускает набор слишком многих конформаций и выбор какой-либо из них осуществляется чисто интуитивно. В этом подходе все взаимодействия между атомами игнорируются, за исключением вандерваальсовых сил отталкивания, которым соответствует бесконечная энергия при перекрывании атомов и нулевая энергия в остальных случаях. Однако при усложнении такого подхода путем количественного учета других хорошо изученных взаимодействий, например водородных связей, оказывается удобно изучать конформации стереорегулярных молекул. Именно благодаря такому комбинированному подходу Полинг и Кори предсказали существование а-спирали и β-структуры в белках, а Уотсон и Крик — двойную спираль ДНК.
Модель твердых сфер встречается на практике при построении объемных моделей молекул. В ЭВМ (компьютер) вводят следующее выражение:
![]()
где энергия Е конформации X равна сумме парных взаимодействий всех атомов молекулы; с помощью индексов і и j учитываются все атомы от первого до последнего, а еij зависит от типа атомов і и j. Энергия взаимодействия еij между атомами і и j может быть представлена разными способами, и один из них отвечает модели твердых сфер:
![]()
Здесь еij — функция расстояния eij между центрами атомов; она имеет разрыв при rij = Rij (Rij — сумма вандерваальсовых радиусов атомов і и j). Радиусы і и j определяются только типом атомов (алифатический углерод, кетонный кислород и т.д.). Для простых молекул обычно радиусы атомов находят из величин расстояний между атомами в кристаллической решетке. В общем случае еij представляет собой функцию потенциальной энергии, зависящую только от набора значений Rij.
Уравнение (21.2) легко распространить па случай наличия водородных связей, тогда разрешенными конформациями считаются те, в которых: а) нет перекрывающихся атомов и б) присутствует максимальное число водородных связей.
Ограничения модели твердых сфер связаны с тем, что реальные атомы не являются ни жесткими, ни сферическими. Более того, в молекулах действуют также иные силы, а не только стерическое отталкивание. Как отмечалось выше, учет водородных связей совершенно необходим, чтобы модель твердых сфер реже применялась в самом примитивном виде. В молекулах существенную роль играют электростатические взаимодействия, возникающие между атомами, несущими единичный или дробный заряд, обусловленный различием электроотрицательности атомов. Эти взаимодействия нельзя, однако, описать с помощью простой функции от rij, имеющей разрыв. Уместно отметить также, что модель твердых сфер вообще может применяться только потому, что области с наибольшей электронной плотностью не изменяются радикальным образом при объединении изолированных атомов в молекулу. Однако отклонение формы атомов от сферической, возможность образования водородных связей, а также дробные заряды, локализованные на атомах,— все это и есть те заметные изменения, которые происходят с атомами при их объединении в молекулы.
Модель деформируемых (мягких) сфер также основана на уравнении (21.2), но здесь еij — непрерывная функция от rij. Вообще говоря, непрерывные потенциальные функции выполняют роль не более чем аналитических соотношений, выражающих примерную зависимость изменения энергии от rij, и совсем не обязательно вкладывать какой-либо физический смысл в отдельные составляющие функции.
Тем не менее в известной степени удобно и оправданно представлять непрерывную потенциальную функцию в виде суммы вкладов, каждый из которых отвечает либо энергии вандерваальсова отталкивания, либо энергии электростатического взаимодействия, либо энергии водородной связи и т. д. Используемые потенциальные функции могут быть записаны в виде различных математических выражений; с учетом современных обозначений наиболее простое выражение для энергии eij можно записать в следующем общем виде:
![]()
Здесь Аij, Bij, Cij — параметры, зависящие от типов двух взаимодействующих атомов (алифатический углерод, кетонный углерод и т. п.). Вклад А в основном определяет потенциальную энергию модели твердых сфер [уравнение (21.2)], поскольку с увеличением показателя а зависимость от расстояния rij первого слагаемого в уравнении (21.3) быстро растет. Однако, чтобы значение функции еij с ростом rij быстрее сходилось к нулю, требуется дополнительная составляющая В, которую обычно истолковывают как вклад, отвечающий за слабые вандерваальсовы силы притяжения между взаимодействующими атомами (дисперсионные силы Лондона, вызываемые возникновением наведенных дипольных моментов). Величина этого вклада по сравнению с общей ошибкой вычислений достаточно мала, и основная роль второй составляющей — обеспечить равенство близкодействующих сил на коротких расстояниях. Третья составляющая энергии С отвечает за кулоновское электростатическое взаимодействие, обусловленное наличием дробных зарядов, помещаемых для простоты в центры атомов. Энергия водородной связи не представлена в виде отдельной составляющей, так как в биологических молекулах этот вид взаимодействий можно отнести к электростатическим. Поэтому при использовании уравнения (21.3) энергия и ориентация водородной связи не учитываются.
Две первые составляющие (А и В) всегда вместе присутствуют в уравнении (21.3), и вторая из них обеспечивает наличие минимума функции потенциальной энергии. Пусть еijvw — энергия межатомного вандерваальсова взаимодействия [т. е. уравнение (21.3) без третьего слагаемого — электростатического вклада]. Способ определения значений Аij и Вij для различных пар атомов более удобен, если эти параметры представлены в виде функции еij0 (минимальное значение eijvw) и rij (расстояние, при котором имеет место этот минимум). Существование минимума обусловлено тем, что а>b, и соответствует равновесному расположению пары атомов і и j, т. е. случаю, когда значительные силы отталкивания и слабые силы притяжения уравновешивают друг друга. Заметим, что в реальной молекуле вследствие наличия взаимодействия между остальными парами атомов такая ситуация может только случайно отвечать равновесной. Тем не менее можно записать:
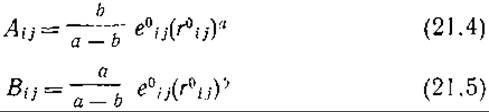
Здесь rij играет более существенную роль, чем eij0, которая близка к 0,4 кДж/моль, и результаты расчетов мало зависят от ошибки определения последней величины. Параметр rij0 должен, очевидно, зависеть от размера атомов и принимается равным сумме вандерваальсовых радиусов Rij. Однако радиусы атомов, наблюдаемые в кристаллах, редко соответствуют равновесным из-за наличия других взаимодействий, включая электростатические, которые и обусловливают особенности данной кристаллической упаковки. Обычно, если принять rij0 = Rij, величины rij0 оказываются слишком заниженными; поэтому для некоторых применений были испытаны и более сложные способы определения параметров [17]. Но при всех способах расчета с использованием уравнения (21.3) достигается более правильный учет влияния размеров атомов по сравнению с моделью твердых сфер.
Последнюю составляющую энергии обычно представляют в виде
![]()
где qіи qj — парциальные заряды на атомах і и j, а ε — параметр, соответствующий диэлектрической проницаемости. В то время как присутствие в уравнении (21.6) произведения qi∙qj-представляется теоретически вполне обоснованным, использование здесь параметра є вызывает некоторые сомнения. Скорее є можно рассматривать просто как некоторый вспомогательный множитель, призванный привести в соответствие расчетные и экспериментальные данные, поскольку очень редко наблюдается совпадение значения є со значением макроскопической диэлектрической проницаемости системы. При квантовомеханических расчетах, а также интерпретации данных при экспериментальных исследованиях обычно принимают ε=1. До недавнего времени при относительно простых вычислениях, как правило, испытывали все значения є от единицы до бесконечности и анализировали влияние этого параметра па получаемые результаты. В последние годы, кроме этого, учитывают несколько различных моделей растворов.
a, b и с — расчетные константы. В разных работах используются различные наборы этих констант; потенциальные функции классифицируют с помощью набора этих констант, например 12-6-1, 9-6-1, 9-6-2 и т. д. Имеются серьезные теоретические основания для выбора b = 6 и с=1, хотя при учете водородной связи или в целях экономии расчетного времени (rij2 вычисляется из значений атомных координат быстрее, чем rij) иногда принимают с>1. Выбор значения а вызывает большие затруднения, так как для вычисления составляющей А теоретически более оправданно использование экспоненциальной функции Aijехр(—μif∙rij). Однако при грубых расчетах, если значение а достаточно велико, можно этого не делать. Экспоненциальная функция используется редко, так как в нее входит дополнительный параметр μij; кроме того, на вычисление этой функции требуется больше машинного времени. Следует отметить, что Аij, Bij, Cijзависят от а, b, с и при любом изменении последних необходимо проводить расчеты заново.
Модели твердых сфер и модель деформируемых (мягких) сфер используют почти всегда в приближении жесткой геометрии. Это означает, что при изменении конформации и поиске минимума конформационной энергии разрешается варьировать только двугранные углы вращения вокруг одиночных связей. Длины связей, валентные и торсионные углы при двойных и тройных (или частично двойных или тройных) связях обычно считаются неизменными и равными значениям, полученным из кристаллографических данных. При этом считается, что последние отвечают равновесному состоянию, для выхода из которого требуется значительная энергия. Принимаемые ограничения оправдываются двумя практическими соображениями, во-первых, расчетная задача существенно упрощается, так как сокращается число рассматриваемых конформаций, и во-вторых, выполняемые расчеты становятся нечувствительными к взаимодействиям, отвечающим за энергию валентных связей. Важнее всего, что при этом не учитывается вклад в конформационную энергию изменений длин связей и валентных углов.
Таблица 21.1. Параметры Хаглера — Хьюлера — Лифсона при использовании потенциальной функции 9-6-1а
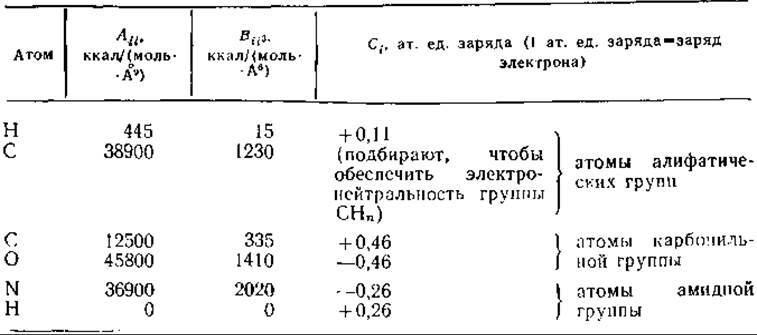
а Используется в уравнении ![]()
![]()
Значения параметров получены Хаглером с сотр. [17] и Хаглером и Лифсоном [15] из данных для кристаллов пептидоподобных молекул. Было показано, что приведенные значения параметров хорошо согласуются с экспериментальными данными о конформационных возможностях молекул [67] и квантовомеханическими расчетами ab initio [24]. Данные можно использовать при расчетах в приближении валентного силового поля (см. ниже). Хотя приведенный набор параметров заслуженно считается одним из лучших, в каждом конкретном случае он был уточнен в лаборатории автора и лаборатории Хаглера.