Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Кинетика катализируемых ферментами реакций
Определение констант скоростей элементарных стадий ферментативной реакции
Релаксационные методы изучения кинетики

В этом разделе мы несколько подробнее остановимся на релаксационных методах, основанных на скачкообразном изменении условий реакции. Теория и практика релаксационных методов была разработана также в применении к осциллирующим возмущениям условий реакций. Сначала рассмотрим равновесие только между субстратом, ферментом и фермент-субстратным комплексом:

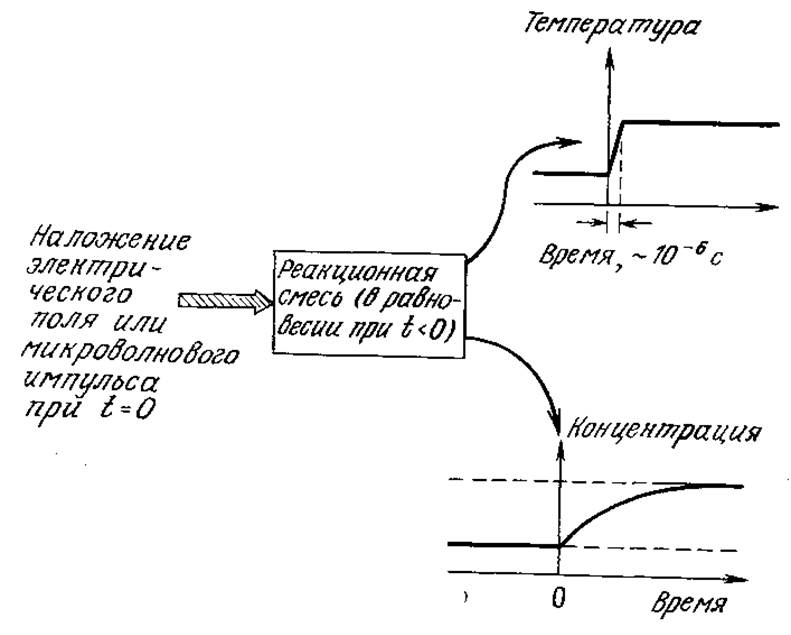
РИС. 3.13. В релаксационных методах небольшое скачкообразное изменение условий реакции, например температуры, вызывает быстрый переход в новое равновесное состояние.

Мы знаем, что для этой реакции

S + (es) =s₀ и е + (es) = е₀

Поэтому для эффективно перемешиваемой реакционной смеси, находящейся в реакторе периодического действия, уравнение материального баланса для s

принимает форму

Если мы символом s* обозначим концентрацию s в равновесном состоянии после скачкообразного изменения условий реакции, то s* можно определить, решив уравнение

f(s*)= 0      (3.30)

где f(s)—правая часть уравнения (3.29), равная dsjdt. В любом релаксационном эксперименте s будет близко s*, и приближенно можно считать, что f(s) равно первым членам в разложении Тейлора типа

(s—s*)+члены порядка (s—s*)²и высших порядков. (3.31)

Здесь f(s*), согласно уравнению (3.30), равно нулю. Обозначив символом χ отклонение от равновесной концентрации

χ = s — s*      (3.32)

и принимая во внимание, что s* не зависит от времени, путем преобразования уравнений (3.29) — (3.32) можно получить линейное уравнение следующего вида [если пренебречь членами второго и высшего порядков в уравнении (3.31)]:

Если система сначала находится в состоянии исходного равновесия, которое отвечает условиям, предшествующим скачкообразному возмущению, то

χ(0) = ∆χ₀      (3.34)

а затем

где

В уравнении (3.36) е* выражает концентрацию не связанного в комплекс фермента в состоянии конечного равновесия. Уравнение (3.35) свидетельствует о том, что т можно определить по наклону прямой, отражающей полулогарифмическую зависимость χ(t) от ∆χ₀. Другими словами, τ представляет собой время, в течение которого χ(t) уменьшается до 37% от своего первоначального значения. Определив τ, χ* и е* (или е₀ и s₀), далее по уравнению (3.36) можно найти взаимосвязь между k₁ и k_-1, не зависящую от уравнения равновесия. Таким путем можно вычислить как k₁, так и k_-1.

Этот метод нашел широкое применение в химической кинетике, в том числе и в кинетике рассматриваемого здесь ферментативного катализа.