Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Кинетика катализируемых ферментами реакций
Другие факторы, влияющие на ферментативную активность
Скорость ферментативных реакций и температура

При изучении любых проблем химической кинетики одним из основных теоретических положений является уравнение Аррениуса, выражающее зависимость константы скорости реакция от температуры:

где Е_а — энергия активации реакции; R — газовая постоянная; А — предэкспоненциальный множитель; 7 — абсолютная температура.

При графическом изображении зависимость Ink от 1/7 выражается прямой с тангенсом угла наклона — E_a/R [конечно, если соблюдается условие уравнения (3.66)]. Аррениусовской зависимости константы скорости реакции от температуры подчиняются и многие реакции, катализируемые ферментами; примером могут служить экспериментальные данные, представленные на рис. 3.24.

Следует подчеркнуть, однако, что температурный диапазон, в котором были получены приведенные на рис. 3.24 данные, очень узок. В этом эксперименте не рассматривались температуры, значительно превышающие обычные в биологических условиях пределы. Что же произойдет, если мы попытаемся заставить фермент катализировать процесс еще быстрее, подняв температуру еще выше? Как показано на рис. 3.25, в большинстве случаев результат окажется очень печальным.

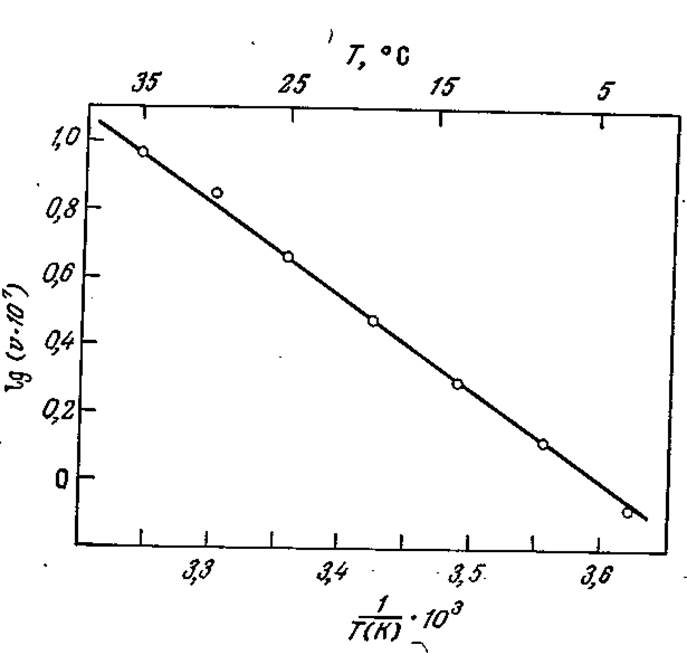
РИС. 3.24. Аррениусовская зависимость скорости ферментативной реакции (катализируемый миозином гидролиз АТР) от температуры. [Воспроизведено из работы: Laidler К. J., The Chemical Kinetics of Enzyme Action, p. 197, The Clarendon Press, Oxford, 1958; данные из статьи Quellet L., Laidler K. Morales M. F., Molecular Kinetics of Muscle Adenosine Triphosphate, Arch. Biochem. Biophys., 39, 37 (1952).]

Денатурация большинства белков начинается в диапазоне температур от 45 до 50 °С и завершается очень быстро при 55°С. Один из механизмов термической денатурации белков очевиден: по мере повышения температуры атомы в молекуле белка приобретают все более высокую энергию, в том числе кинетическую, и в конце концов становится возможным разрушение слабых связей, стабилизирующих глобулярную структуру белка, что и приводит к его инактивации.

Термическая инактивация ферментов может быть обратимой, необратимой или смешанной. Зависимость скорости реакции ферментативного катализа от температуры в достаточно широком диапазоне температур может быть описана с помощью простой модели обратимой термической инактивации. Согласно этой модели, мы принимаем, что неактивная (і) и активная (а) формы фермента находятся в равновесии:

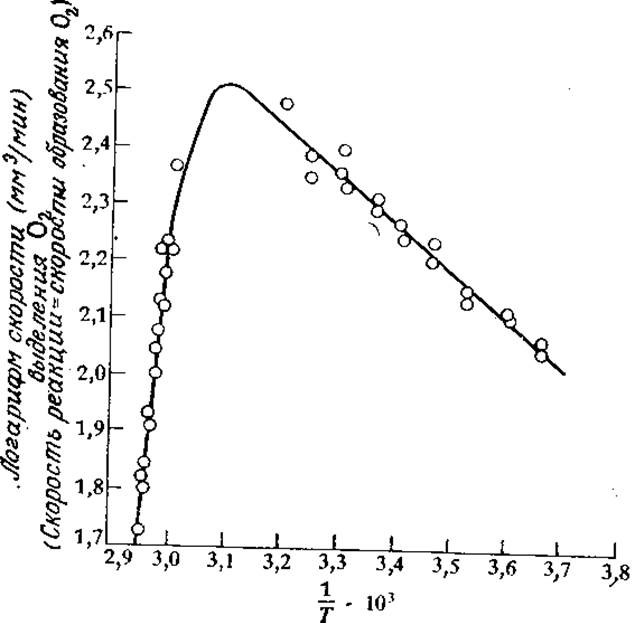
РИС. 3.25. При высоких температурах, когда начинает доминировать процесс термической инактивации фермента, аррениусовская зависимость скорости реакции от температуры нарушается (приведен пример разложения Н₂О каталазой). Сплошная кривая вычислена по уравнению (3.73) при следующих значениях параметров: E = 3,5 ккал/моль, ∆H_d = 55,5 ккал/моль, ∆S_d = 168 ккал/(моль∙К), ß = 258 мм³/мин. [Воспроизведено из статьи: Sizer I.W., Temperature Activation and Inactivation of the Crystalline Catalase-Hydrogen Peroxide System, J. Biol. Chem., 154, 461 (1944).]

Константу равновесия этой реакции можно выразить следующим уравнением:

В этом уравнении символами ∆G_d, ∆Н_d и ∆S_dобозначены свободная энергия, энтальпия и энтропия инактивации соответственно.

Хотя изолированные водородные связи сравнительно слабы (их энергия обычно изменяется в пределах от 3 до 7 ккал/ /моль), энтальпия инактивации ферментов ∆Нd достаточно высока, составляя, например, для трипсина и лизоцима белка куриных яиц соответственно 68 и 73,5 ккал/моль. Инактивация этих ферментов сопровождается изменением энтропии, равным + 213 кал/(моль∙К). Благодаря высокой энтальпии денатурации уже небольшие изменения температуры существенно изменяют относительное количество активной формы фермента. При таких высоких значениях ∆Н_d фермент инактивируется практически полностью в диапазоне тридцати градусов.

Поскольку весь фермент существует либо в активной, либо в неактивной форме, т. е.

e_а + e_i = e₀      (3.69)

из уравнения (3.68) следует, что

Согласно теории переходного состояния, скорость реакций (3.4) при высоких концентрациях субстрата может быть выражена следующим образом:

v_max = e_a∙k(T)      (3.71)

где

Здесь k_B и h — константы Больцмана и Планка соответственно, а а — коэффициент. Из уравнений (3.68), (3.70) — (3.72) следует, что

В уравнении (3.73) коэффициент ß включает a, k_B, h, е₀ и ехр(∆S*/R).

Это уравнение и представляет собой математическое выражение, описывающее схематично изображенное на рис. 3.25 поведение систем фермент — субстрат. Показанная на этом рисунке сплошная линия, проходящая через экспериментально найденные точки, фактически была вычислена по уравнению (3.73) после определения параметров ß, Е, ∆S_d и ∆Н_d на основе тех же экспериментальных данных. При больших значениях 1/Т тангенс угла наклона кривой приближенно равен —Е/R (погрешность равна Т (К) и обычно не вносит большого вклада). Тангенс угла наклона другого прямого участка кривой при более высоких температурах равен приблизительно (∆На—Е)/ R. Величину ∆S_d можно определить, используя тот факт, что при температуре Т_mах, когда lnv_max принимает наивысшее значение,

[Это выражение легко получить, приняв d(lnv_max)/d_T равным нулю.] Поскольку Т_max известна из измерений, а величины Е и ∆Н_d мы уже определили, то не представляет труда вычислить правую часть уравнения (3.74). Теперь, зная величину K_d(T_mах), возвратимся к уравнению (3.68) и найдем AS_d. Наконец, подберем такое значение коэффициента ß, чтобы v_mах [T_mах в уравнении (3.73)] стало равным измеренной величине. При необходимости более точные значения параметров можно получить методом последовательного приближения. В частности, очень большое влияние на результаты может оказывать значение Тmax. Конечно, от температуры зависят и другие параметры уравнений скорости реакции, например константа Михаэлиса или ингибиторная константа. Если эти параметры считать константами равновесия, как это часто бывает в действительности, то мы должны прийти к температурной зависимости типа той, которая выражается уравнением (3.68). Тогда график зависимости lnК (или рК) от 1/T будет представлять собой прямую линию, по наклону которой можно определить стандартную свободную энергию.

В некоторых случаях графическая зависимость в этих координатах изображается не прямой линией, иными словами, наклон линии меняется при изменении диапазона температур. Причиной подобных осложнений могут быть неоправданные упрощения в интерпретации К_m или K_iили даже в последовательности катализируемых ферментом реакций. Напомним, например, что для случая простейшей последовательности реакций (3.4) К_m представляет собой не что иное, как отношение констант скоростей элементарных стадий реакции, выражаемое уравнением (3.5). Если каждую из этих констант элементарных стадий в свою очередь выразить в форме уравнения Аррениуса [уравнение (3.66)] или в форме уравнения теории переходного состояния [уравнение (3.72)], то получится весьма сложная форма зависимости от температуры. Другим возможным источником затруднений в определении зависимости некоторых параметров скорости реакции от температуры может служить существование нескольких промежуточных фермент-субстратных комплексов (или комплексов фермента с продуктом реакции).

Подобные соображения были положены в основу полезного и довольно широко применяемого способа проверки корректности кинетических моделей и соответствующих гипотетических последовательностей реакций. Если зависимость кинетических параметров в аррениусовских координатах выражается не прямой, то исходная модель или чрезмерно упрощена, или вообще неверна.