Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Применение реакций, катализируемых ферментами
Кинетика реакций, катализируемых иммобилизованными ферментами
Моделирование диффузии и реакций внутри частицы катализатора

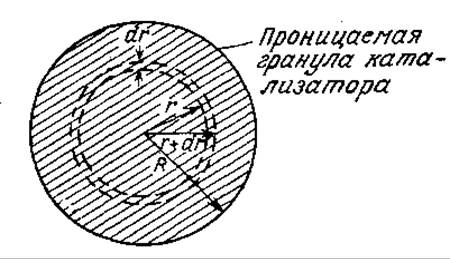
Как мы уже не раз упоминали выше, обычно ферменты иммобилизуют путем связывания с внутренними поверхностями пористых носителей или путем включения в матрицы, через которые может диффундировать субстрат. В таких системах для расчета наблюдаемой скорости трансформации субстрата необходимо знать профиль изменения его концентрации в частице катализатора. Для этого в свою очередь прежде всего надо найти уравнение материального баланса в стационарном состоянии для тонкого слоя проницаемого катализатора. Предположим, что фермент иммобилизован в грануле, форму которой можно считать сферической. Тогда необходимый тонкий слой будет заключен между двумя концентрическими сферами радиусов r и r+dr соответственно (рис. 4.20). Толщина этого слоя настолько мала, что все условия внутри него можно считать постоянными независимо от положения.

Символами D_es и v обозначают эффективный коэффициент диффузии субстрата и локальную скорость его трансфорхмации соответственно. Оба этих параметра принципиально отличаются от аналогичных параметров для процессов в растворе; существенна и количественная разница между ними. Рассмотрим сначала эффективный коэффициент диффузии, учитывая, что скорость диффузии любых веществ через носитель зависит от следующих факторов:

1. Часть поперечного сечения частицы катализатора занята молекулами твердого носителя и поэтому не может использоваться для диффузионного транспорта субстратов (соответствующий параметр — пористость частицы ε_р).

2. Сеть пор переплетена очень сложным образом, поэтому диффузия может происходить только в разрешенных, часто меняющихся направлениях (соответствующий параметр — коэффициент извилистости τ).

3. Поры могут иметь очень небольшой диаметр, сравнимый с размерами молекул субстрата (ограниченная диффузия; соответствующий параметр К_p/К_r).

Уравнение материального баланса для стационарного состояния в тонком слое, ограниченном радиусами r и r+dr, можно записать в следующем виде:

Если принять, что эффективный коэффициент диффузии субстрата Des постоянен, то, разделив на 4пdr, получим

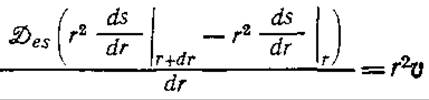
В пределе при dr→0

или

РИС. 4.20. Вывод уравнения стационарного состояния сферической проницаемой гранулы иммобилизованного фермента с помощью концепции тонкого слоя.

Теперь мы можем выразить эффективный коэффициент диффузии через эти параметры:

Здесь Ds₀ — коэффициент диффузии субстрата в жидкой реакционной среде. Параметр пористости ε_р необходимо определять экспериментально для каждого конкретного носителя. Для коэффициента извилистости обычно принимают значения, расположенные в диапазоне от 1,4 до 7. Что касается ограниченной диффузии, то соответствующий параметр К_р/К_r в первом приближении можно оценить, воспользовавшись следующим уравнением:

где r_s и r_р— (эквивалентный) радиус молекул субстрата и характеристический радиус поры соответственно. Неопределенность всех параметров в правой части уравнения (4.14) является причиной того, что найти достоверное значение D_es расчетным путем очень трудно. Поэтому предпочтительнее оценивать D_еs на основе экспериментального изучения общей кинетики процесса. Этот метод мы рассмотрим позднее, после анализа взаимного влияния диффузионных и химических процессов внутри частицы иммобилизованного фермента.

Следует отметить также, что массопередача внутри частицы может зависеть от химии ее внутренних поверхностей и от наличия ионизированных групп. Более того, если в реакции участвуют или образуются ионизированные соединения, то внутри частицы катализатора могут создаваться градиенты электрического потенциала, которые в свою очередь будут изменять скорости транспорта заряженных веществ. Методы анализа и учета этих факторов читатель может найти в литературе, приведенной в конце главы.

Если допустить, что собственная кинетика локальной ферментативной реакции с участием иммобилизованного фермента подчиняется уравнению Михаэлиса — Ментен:

то параметр максимальной скорости в данном случае можно определить как произведение нагрузки носителя ферментом е_imm (количество микромолей фермента в 1 г носителя) на удельную активность иммобилизованного фермента q_Eimm (число микромолей субстрата, превращаемых в 1 с 1 мкмолем фермента) и на плотность частиц р_р (количество граммов носителя в единице его объема):

Напомним, что иммобилизация может изменять структуру фермента и (или) его молекулярное окружение, и, следовательно, величины g_E,іmm и К_m для иммобилизованного фермента могут отличаться от соответствующих величин для фермента в растворе. Как мы уже отмечали в разд. 4.4.1, собственную кинетику фермента желательно изучать в условиях минимального вклада в общую кинетику системы эффектов, обусловленных массопередачей. Критерий для таких лимитируемых реакцией условий мы найдем в ходе приведенного ниже анализа.

Уравнение материального баланса по субстрату в стационарном состоянии, вывод которого приведен на рис. 4.20, представляет собой обычное дифференциальное уравнение второго порядка:

Изображенную на рисунке модель необходимо дополнить граничными условиями. Профиль изменения концентрации в частице катализатора почти всегда симметричен относительно центра сферы, т. е.

В этом анализе мы допускаем, что концентрация субстрата на наружной поверхности гранулы равна концентрации субстрата s₀ в жидкой среде, омывающей гранулу. (Случаи одновременного сопротивления массопередаче в граничном слое и внутри частицы будут рассмотрены в следующем разделе.) Следовательно,

Наблюдаемая общая скорость v₀ утилизации субстрата частицей катализатора равна поступлению субстрата в гранулу за счет диффузии. Величина v₀, выраженная в молях на единицу объема гранулы в единицу времени, составляет

Здесь символами V_p и А_р обозначены объем частицы и площадь ее наружной поверхности соответственно. Как и в предыдущем разделе, такие скорости мы будем выражать в виде безразмерного параметра, определяющего влияние диффузионных эффектов. Коэффициент эффективности η определяется как

К сожалению, если в соответствии с уравнением (4.16) у изменяется нелинейно, то определить коэффициент эффективности аналитическим путем непросто. Для этого необходимо решить в цифровой форме задачу о граничном значении [уравнения (4.18) — (4.20)] и затем по уравнению (4.21) найти v₀. Такие вычисления достаточно сложны и трудоемки, поэтому мы постараемся выразить результаты в наиболее простой и в то же время достаточно общей форме. Для этого преобразуем приведенные выше уравнения в эквивалентные безразмерные выражения.

Введем параметры тогда уравнение (4.18) можно записать в следующей форме:

Здесь безразмерные параметры ø и ß определяются как

Соответствующие уравнению (4.23) безразмерные граничные условия равны

Физический смысл параметра ø, называемого модулем Тила, заключается в том, что квадрат модуля Тила представляет собой частное от деления скорости реакции первого порядка R³(v_max/K_m)s₀ на скорость диффузии RD_ess₀. Параметр насыщения (1 является мерой отклонения локальных скоростей от кинетики первого порядка, причем большие значения ß свидетельствуют о том, что порядок реакции приближается к нулевому.

Выразим через эти безразмерные переменные коэффициент эффективности

Согласно уравнениям (4.23) и (4.25), является функцией только и поэтому зависит только от β и ø. Учитывая уравнение (4.26), отсюда следует, что η зависит только от модуля Тила и параметра насыщения:

При использовании выражения (4.27) для оценки коэффициента эффективности возникает проблема, связанная с тем, что собственные параметры кинетики каталитической реакции v_max и К_m часто неизвестны. С помощью простых преобразований можно показать, однако, что при определении η можно обойтись и без первого параметра v_max. Действительно, из уравнений (4.26) и (4.21) следует, что

Подстановка этого выражения в правую часть уравнения (4.27)

приводит к уравнению (4.28), отражающему неявную зависимость между η, ß и новым безразмерным наблюдаемым модулем Ф, который определяется следующим образом:

(Обратите внимание на то, что Ф зависит только от наблюдаемой общей скорости v₀ и не зависит от собственных кинетических параметров каталитической реакции.) Решение этого неявного уравнения позволяет определить η как функцию от ß и наблюдаемого модуля Ф:

η = g(Ф, ß)      (4.29)

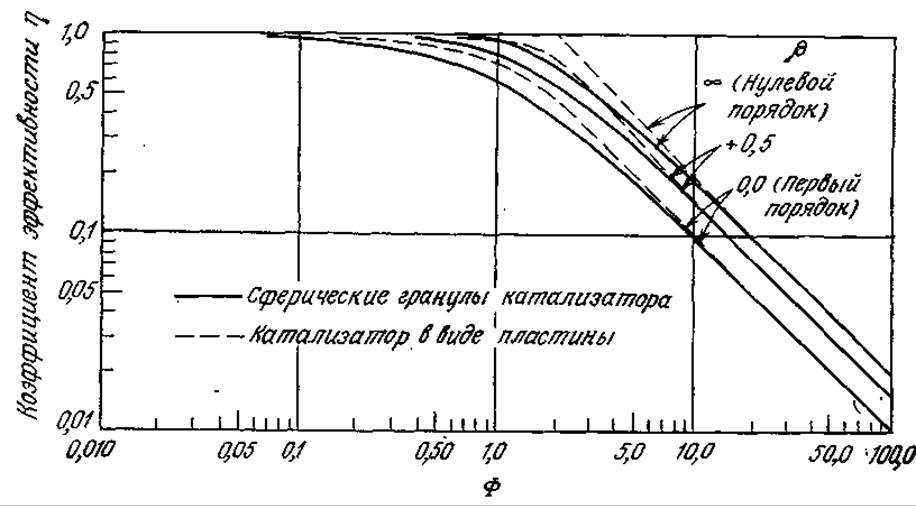
РИС. 4.21. Коэффициенты эффективности иммобилизованных ферментных катализаторов с собственной кинетикой, описываемой уравнением Михаэлиса — Ментен (ß=so/Km). Определение безразмерного наблюдаемого модуля Ф дано в уравнении (4.28).

На рис. 4.21 приведены графики зависимости η от Ф, выражаемые уравнением (4.29) при ß → 0 и ß→∞. Поскольку коэффициенты эффективности для промежуточных значений K_m/s₀ располагаются между кривыми для этих двух предельных случаев, нетрудно видеть, что коэффициент η сравнительно не чувствителен К последнему собственному параметру K_m/s₀.

Прежде чем перейти к изучению аналитических решений, основанных на приближенной оценке кинетики процессов, нам нужно найти выражение для η, применимое при больших значениях Ф (или ø) и кинетике, выражаемой уравнением Михаэлиca — Ментен. Если модуль Ф достаточно велик (Ф≥3; см. табл. 4.15), то субстрат быстрее утилизируется ферментом, чем диффундирует внутрь гранулы катализатора. В такой ситуации, когда скорость всего процесса определяется скоростью диффузии, можно допустить, что весь субстрат трансформируется в граничащем с наружной поверхностью тонком слое гранулы катализатора, поэтому эффектом кривизны (2/r∙ds/dr) в уравнении (4.18) можно пренебречь. Отсюда следует, что

Таблица 4.15. Критерий для оценки влияния эффектов массопередачи на кинетику всего процесса

Если в уравнение (4.30) вместо d²s/dr² подставить правую часть уравнения (4.31)

и затем интегрировать по s, то мы получим следующее выражение:

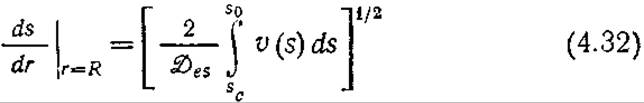
Здесь s_c и s₀— концентрации субстрата в центре частицы (r = 0) и на ее поверхности (r = R) соответственно.

В случае лимитируемой диффузией реакции s_c ≈ 0, что позволяет вычислить интеграл в уравнении (4.32). Совместное решение уравнений (4.21), (4.22) и (4.32) приводит к следующему выражению для коэффициента эффективности, справедливому при достаточно больших значениях Ф или ø:

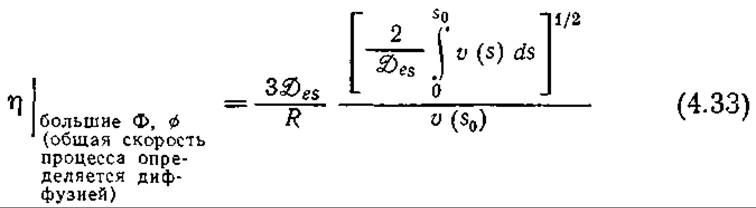
Преобразование этого уравнения для частного случая кинетики, выражаемой уравнением Михаэлиса — Ментен (4.16), дает

Продолжая изучение кинетики, выражаемой уравнением Михаэлиса — Ментен, отметим, что если допустить первый порядок реакции (это справедливо при s ≪ K_m), то, согласно данным, приведенным на рис. 4.21,

v = ks      (4.35)

где k = v_mах/K_m, и η принимает консервативное (низкое) значение, достаточно близко приближающееся к истинному значению. Воспользовавшись линейной зависимостью (4.35), мы можем решить аналитическим путем уравнения модели лимитируемого диффузией процесса; таким образом получим

В этом выражении модуль Тила Ф равен

С помощью уравнения (4.37) можно получить изображенную на рис. 4.21 кривую, отвечающую реакции первого порядка, если использовать справедливую в такой ситуации зависимость:

Другой предельный случай кинетики Михаэлиса — Ментен характерен для реакций, порядок которых приближается к нулевому (s ≫ K_m); такую ситуацию можно определить следующим образом (k₀ = v_max):

Совместное решение задачи о граничном значении [уравнения (4.18)—(4.20)] и функции утилизации фермента показывает, что концентрация субстрата s зависит от радиуса r следующим образом:

Это выражение справедливо при всех неотрицательных значениях s, т. е. в интервале от r = R до некоторого критического радиуса r = R_c, определяемого путем решения уравнения (4.18) совместно с уравнением (4.20) при следующих граничных условиях:

Это решение приводит к кубическому уравнению относительно R_c:

Таким образом, если уравнение (4.42) имеет положительный корень (R_c/R), величина которого меньше единицы, то внутри гранулы катализатора существует некоторая область (от r = 0 до r = R_c), в которой s = 0 и у = 0. В таких случаях реакция протекает только во внешнем слое частицы (R_c < r ≤ R), так что

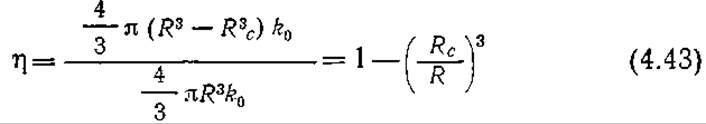
Если не существует имеющего физический смысл решения уравнения (4.42), то η = 1 и скорость трансформации субстрата во всем объеме гранулы катализатора одинакова.

Другим важным следствием изображенных на рис. 4.21 зависимостей является малое влияние геометрии частицы катализатора на взаимозависимость η и ø. Например, коэффициент эффективности реакции первого порядка в пластине определяется выражением

Здесь Ф определяется по уравнению (4.37) при V_p/A_p, равном половине толщины пластины. Эта функция во всем диапазоне значений Ф отличается от функции в уравнении (4.36) не более чем на 10%. Наибольшие отличия наблюдаются при ø, близком единице; с возрастанием или убыванием ø эта разница быстро уменьшается. Незначительное влияние геометрии частиц катализатора на функцию η = f(ø) часто позволяет использовать следующие эмпирические корреляции для коэффициента эффективности пластины иммобилизованного фермента с собственной кинетикой, описываемой уравнением Михаэлиса — Ментен:

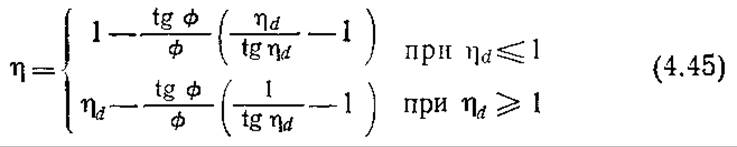
Здесь η_d — асимптотическое значение коэффициента эффективности, определяемое по уравнению (4.34). Эти корреляции, первоначально разработанные для катализаторов с частицами, имеющими форму пластин, можно применять и к другим симметричным геометриям частиц, используя в формулировке модуля Тила в качестве параметра характеристической длины частное от деления объема частицы на ее наружную поверхность.

Малая чувствительность функции η к изменениям порядка реакции и геометрии частиц катализатора явилась основой удобного общего критерия, позволяющего различать лимитируемые реакцией и лимитируемые диффузией процессы. Этот критерий (табл. 4.15) сводится к единственному параметру Ф, который, как мы знаем, зависит только от наблюдаемых переменных. Подробнее этот критерий рассмотрен в работе [21].

В небиологическом катализе параметр η обычно рассматривают как меру эффективности использования катализатора. Если η существенно отличается от единицы, то общая скорость процесса может быть повышена путем измельчения катализатора; при этом Ф уменьшается и, следовательно, возрастает η. Такой подход может оказаться полезным и в биологическом катализе; во всяком случае, он указывает на наличие связи между размером частиц иммобилизованного фермента и максимальной эффективностью процесса.

Непосредственное изучение собственной кинетики также возможно только в тех случаях, когда фактор эффективности близок единице. На катализаторе с достаточно малыми размерами частиц (см. упражнение 4.5) можно экспериментально определить характер изменения скорости катализируемой иммобилизованным ферментом реакции и найти значения соответствующих кинетических параметров. Эта информация необходима для расчета наблюдаемой общей кинетики реакции на более крупных частицах катализатора. Поскольку в водных растворах эффективные коэффициенты диффузии субстрата и (или) общие концентрации субстрата обычно невелики, то лимитируемый диффузией режим, как правило, обусловливается сравнительно большими размерами частиц катализатора, что может быть необходимым или для снижения перепада давлений и сопротивления потоку в реакторах с неподвижным слоем катализатора, или для предотвращения разрушения частиц катализатора в реакторах с псевдоожиженным слоем и со взвесями катализатора. Иногда лимитируемый реакцией режим трудно воспроизвести даже в лабораторных условиях. В таких случаях данные о собственных кинетических параметрах иммобилизованного фермента приходится получать описанным выше аналитическим путем на основе экспериментальных данных, усложненных диффузионными эффектами. Как это показано ниже на конкретном примере, экспериментальное изучение кинетики реакций, катализируемых иммобилизованными ферментами, позволяет оценить и эффективный коэффициент диффузии субстрата.

Пример 4.3. Определение эффективного коэффициента диффузии субстрата и собственных кинетических параметров катализатора на основе иммобилизованного фермента. В качестве исходного положения примем, что собственная кинетика каталитической реакции подчиняется уравнению Михаэлиса — Ментен. Характерные для данного катализатора собственные кинетические параметры v_max и К_m, а также эффективный коэффициент диффузии субстрата D_es можно определить по результатам двух серий кинетических экспериментов, в одной из которых используется катализатор со сравнительно большими частицами (обеспечивающими большие значения ø и, следовательно, лимитируемые диффузией условия), а во второй — катализатор с гораздо более мелкими частицами (достаточно малыми, чтобы скорость трансформации субстрата определялась скоростью реакции). В каждой серии экспериментов необходимо определить значения v₀, отвечающие различным s₀, и затем выразить эти зависимости в графической форме в координатах Эди — Хофсти (зависимость v₀/s₀от v₀; см. разд. 3.2.2). При достаточно больших значениях s₀ реакция имеет нулевой порядок во всем объеме частиц катализатора и, следовательно, коэффициент эффективности равен единице, а кривые для больших и малых частиц катализатора совпадают [это говорит о том, что в случае катализатора с большими частицами условие (4.42) не выполняется и что ограниченная растворимость субстрата не лимитирует эксперименты в диапазоне s₀ ≫ K_m]. Таким образом, независимо от размера частиц кривые будут отсекать на оси абсцисс отрезок, равный v_max.

С другой стороны, если внешняя концентрация субстрата и общая скорость реакции невелики, то собственный порядок каталитических реакций будет приближаться к единице. Тогда для частиц малого размера (лимитируемый реакцией режим) v₀/s₀равно v_max/К_m, а для больших частиц иммобилизованного фермента, т. е. для лимитируемого диффузией режима:

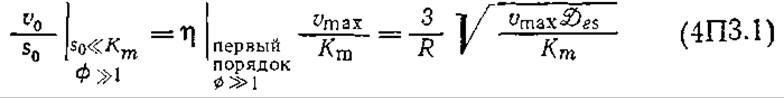
Следовательно, кривая зависимости v₀/s₀ от v₀будет отсекать на оси ординат в случае мелких частиц отрезок, равный V_max/K_m, а в случае больших частиц — отрезок, определяемый уравнением (4П3.1). Таким образом, зная размер больших частиц катализатора и величины трех отрезков, отсекаемых на осях координат кривыми зависимости v₀/s₀от v₀, можно определить v_max, К_m и D_es.

На рис. 4П3.1 представлены результаты применения описанной методики к а-химотрипсину, иммобилизованному на активированной бромцианом сефарозе 4В. Определенные таким образом удельная активность иммобилизованного фермента q_е (q_E — частное отделения v_mах на число молей иммобилизованного активного фермента в единице объема катализатора) и К_m составляют 213 мкмоль субстрата (АТЕЕ, этилового эфира N-ацетил-L-тирозина) на 1 мкмоль активного фермента в секунду и 2,6 мМ соответственно. Эти значения существенно отличаются от соответствующих параметров того же фермента в растворе, составляющих 311 мкмоль АТЕЕ на 1 мкмоль активного фермента в секунду (удельная активность) и 0,73 мМ (К_m); отсюда следует, что иммобилизация заметно изменяет каталитические свойства фермента. Оценка эффективного коэффициента диффузии АТЕЕ в этом катализаторе приводит к величине 3,8∙10^-6 см²/с. Столь малое значение D_es и довольно высокая активность иммобилизованного фермента предполагают существенные диффузионные ограничения даже в случае катализатора с частицами радиусом 60 мкм. Определение модуля Ф этого катализатора дает величину 2,6.

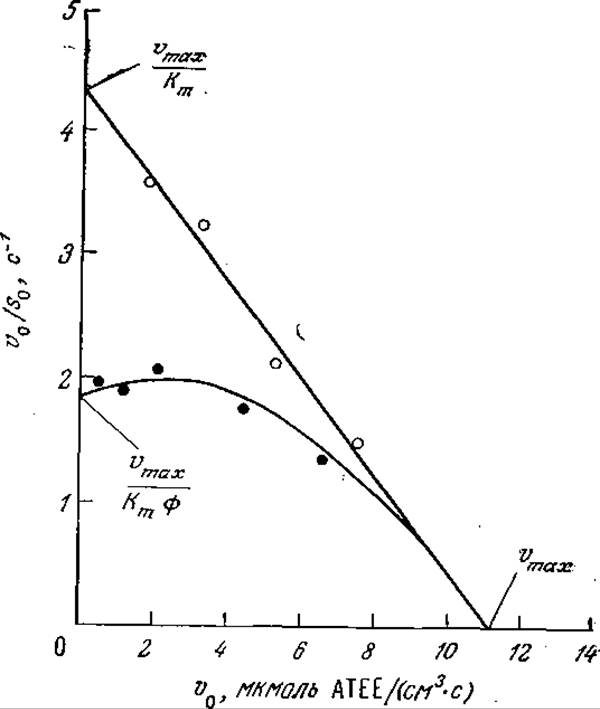
РИС. 4П3.1. Зависимость So/v₀ от v₀ для а-химотрипсина, иммобилизованного на больших (R = 60 мкм; О) и маленьких (R = 10 мкм; О) гранулах активированной BrCN сефарозы 4В. [Экспериментальные данные заимствованы из работы: Clark D. S., Bailey J. Е., Structure-Function Relationships in Immobilized Chymotrypsin Catalysis, Biotech. Bioeng., 25, 1027 (1983).]

При создании катализаторов на основе чрезвычайно дорогих и высокоактивных металлов на носителях обычно стремятся локализовать собственно катализатор в тонком наружном слое частиц носителя. Очевидно, такой же подход применим и при разработке катализаторов на основе иммобилизованных ферментов: используя максимально допустимые для данного процесса размеры частиц носителя, можно обходиться минимальным количеством фермента. Существует несколько методов, принципиально пригодных для получения таких катализаторов. Недавно было показано, что в катализаторах, полученных путем импрегнирования пористого носителя раствором фермента, распределение биокатализатора внутри частицы носителя может быть в высшей степени неравномерным. Как мы увидим в упражнении 4.10, неравномерное распределение фермента влияет на кажущуюся активность и характер инактивации иммобилизованного ферментного катализатора.

Прежде чем перейти к проблеме одновременного сопротивления массопередаче в растворе и внутри частиц катализатора, следует подчеркнуть, что, как и в случае ферментативных реакций в растворе, кинетика катализируемой иммобилизованным ферментом реакции может отличаться от кинетики необратимого превращения одного субстрата, описываемой уравнением Михаэлиса — Ментен. Достаточно полно вопросы анализа кинетики других типов реакций с участием иммобилизованных ферментов освещены в приведенной в конце главы литературе; здесь же мы ограничимся несколькими замечаниями общего характера. Прежде всего следует отметить, что в случае обратимой реакции минимальная концентрация субстрата внутри частицы катализатора равна его равновесной концентрации. Следовательно, при вычислении асимптотического коэффициента эффективности, например по уравнению (4.33), нижний предел интегрирования должен быть равен равновесному значению. Интересно, что в силу различных коэффициентов диффузии разных веществ стехиометрические соотношения внутри частицы катализатора могут отличаться от стехиометрии такого же процесса в растворе. Это явление подробнее рассмотрено в упражнении 4.8.

Изучение систем, в которых скорость процесса определяется как диффузией, так и самой реакцией, мы завершим кратким анализом любопытной ситуации, когда субстрат является ингибитором собственной реакции иммобилизованного фермента. Если внешняя концентрация субстрата s₀ превышает концентрацию субстрата, соответствующую максимальной скорости (см. разд. 3.4.1), то внутри частицы катализатора снижение концентрации субстрата вызовет увеличение локальной скорости реакции до значений, превышающих скорость реакции на внешней поверхности частицы. В этой ситуации при определенных условиях можно наблюдать коэффициенты эффективности, превышающие единицу. Такое на первый взгляд парадоксальное, но в сущности легко объяснимое поведение возможно для любой автокаталитической реакции, т. е. такой системы, в которой скорость реакции возрастает во времени.