Химия и биология белков - Ф. Гауровитц 1953

Величина и форма белковых молекул
Скорость диффузии белков

Когда раствор белка находится в соприкосновении со свободным от белка растворителем, происходит диффузия белковых молекул в растворитель. Количество dS белка, продиффундировавшего через площадь Q за время dt, согласно закону Фика, равно

dS = - DQ(dc/dx)dt,

где dc — изменение концентрации белка на расстоянии dx, dc/dx — градиент концентрации, D — коэффициент диффузии. Порядок величины коэффициента диффузии для аминокислот 10^-5 см^2∙сек^-1, а для белков — от 10^-6 до 10^-7 см²∙ сек^-1. Скорость диффузии пропорциональна абсолютной температуре и обратно пропорциональна величине сопротивления среды, называемой постоянной трения f. Это можно выразить следующим уравнением:

D = RT/Nf,

где R и Т — соответственно газовая постоянная и абсолютная температура, а N — число Авогадро (6,02 ∙ 10²³). Для шарообразных молекул радиуса г постоянная трения пропорциональна радиусу молекулы r и вязкости растворителя η:

f = 6пηr,     (1)

D = RT/Nf = RT/6пηrN.    (2)

Так как объем шара радиуса г составляет 4r³п/3, молекулярный вес шарообразной молекулы белка может быть рассчитан по формуле

М = 4rпNσ/3,

где σ — плотность растворенных белковых частиц. Подставляя r из формулы (2), получаем

М = (4пNσ/3) (RT/6DпηN)³.   (3)

Поскольку молекулы белка в большей своей части не являются шарообразными, их постоянная трения f больше, чем f₀ — постоянная трения шарообразной молекулы того же молекулярного веса. Отношение f/f₀ оказывается, таким образом, больше единицы. Эта величина f/f₀ для частиц правильной формы, таких, как цилиндры, бруски и эллипсоиды, может быть получена расчетным путем. Если же форма молекулы неизвестна, то рассчитать молекулярный вес по скорости диффузии оказывается уже невозможным.

Обычно принимают, что молекула белка представляет эллипсоид вращения с большой осью а и малыми осями 6; ось а может быть и меньше оси b; для вытянутого эллипсоида отношение осей а/b будет больше единицы, для сплющенного эллипсоида — меньше единицы. Отношение осей может быть рассчитано, если М и f/f0 известны. Постоянная трения белка зависит, однако, не только от молекулярного веса и формы молекул, но также от их гидратации, так как набухание растворенной частицы в результате связывания гидратационной воды, естественно, приводит к увеличению сопротивления среды [23].

Если молекула белка имеет шарообразную форму, отношение f/f₀ зависит исключительно от степени гидратации; это может быть рассчитано по формуле

w = (f/f₀ — 1)р/σ,

где w — вес воды, связанной одним граммом белка, р и σ — плотности раствора и растворенного белка соответственно. При расчете молекулярного веса нешарообразных молекул для w обычно принимают значение от 0,3 до 0,5.

Экспериментально постоянную диффузии определяют путем измерения скорости размывания четкой горизонтальной границы, созданной в вертикальной трубке между белковым раствором и растворителем. Это измерение можно провести при помощи одного из оптических приемов, используемых при седиментации и электрофорезе (см. гл. V) [22, 23]. Если исследуемый белок гомогенен, ход изменения градиента концентрации dc/dx будет соответствовать кривой распределения Гаусса, в то время как концентрационный градиент белковой смеси будет отклоняться от этой кривой.

Так как экспериментально создать четкую границу между белковым раствором и растворителем нелегко, оба раствора изучают, разделяя их пористым стеклянным диском [25]. Скорость диффузии измеряют тогда, определяя то количество белка, которое прошло через диск в воду (фиг. 5). При помещении более тяжелого белкового раствора над растворителем диффузия ускоряется силой тяжести. Диффузионный сосудик калибрируется при помощи раствора, коэффициент диффузии которого известен. Если для калибрирования используется белок известного молекулярного веса M₁ с коэффициентом диффузии D₁, то молекулярный вес неизвестного белка М₂, согласно формуле (3), будет равен

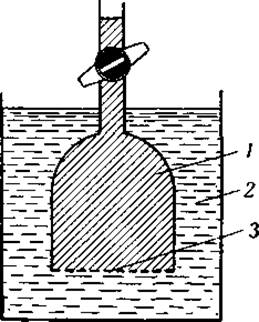
Фиг. 5. Диффузионный аппарат. 1 — коллоидный раствор; 2 — растворитель; 3 — пористый диск.

Если величины f/f₀ и плотности обоих белков одинаковы, то

M₂ = M₁(D₁/D₂)³.

Результаты, полученные этим методом, все же менее надежны, чем результаты, полученные при помощи метода свободной границы.

Молекулярные веса, рассчитанные из скоростей диффузии, дают величины того же порядка, что и значения, полученные для молекулярных весов другими методами.

По причине непостоянства условий, вносимых гидратацией и отклонением от шарообразной формы молекул, определения скорости диффузии редко используются для прямого расчета молекулярных весов. Чаще они сочетаются с методом скорости оседания.