Химия и биология белков - Ф. Гауровитц 1953
Величина и форма белковых молекул
Вязкость белковых растворов
Хорошо известно, что растворы некоторых белков, например желатины, исключительно вязки, в то время как растворы других, например яичного альбумина или сывороточных белков, обладают высокой текучестью даже при концентрациях, значительно более высоких, чем концентрация желатины. Это видно из табл. 3, в которой приведены данные по вязкости водных растворов яичного альбумина [39] при 25,2° и растворов желатины при 37°. При более низких температурах вязкость желатины не может быть измерена, так как растворы желатины превращаются в гель [40].
Таблица 3 Вязкость водных растворов яичного альбумина н желатины
|
Яичный альбумин |
Желатина |
||
|
концентрация, % |
относительная вязкость |
концентрация, % |
относительная вязкость |
|
3,02 |
1,22 |
1 |
2,39 |
|
8,88 |
1,57 |
2 |
3,44 |
|
14,53 |
2,21 |
3 |
4,54 |
|
20,12 |
3,60 |
4 |
5,78 |
|
28,15 |
9,99 |
5 |
7,12 |
|
6 |
9,06 |
||
|
8 |
14,2 |
||
|
10 |
22,0 |
||
Высокая вязкость растворов желатины обусловлена нитевидной формой молекул, которые при броуновском движении захватывают больший объем растворителя, чем шарообразные молекулы того же молекулярного веса. В растворах с асимметричными молекулами требуется поэтому добавочная работа, чтобы сообщить заданную скорость течения.
Определения вязкости проводят очень часто, так как это не сопряжено с какими-либо экспериментальными трудностями. Обычно для этой цели употребляют вискозиметр Оствальда (фиг. 7). Водному раствору белка дают стечь из пипетки 3 через капилляр 4 и определяют время, необходимое для того, чтобы мениск опустился от 1 до 2. Если вязкость белкового раствора не слишком сильно отличается от вязкости воды и если диаметр капилляра подобран правильно, вязкость ті прямо пропорциональна і — времени вытекания — и d — плотности раствора:
η = Сdt.
Если η0 — вязкость воды и η — вязкость белкового раствора, относительная вязкость будет равна
ηoтн = η/η0 = Cdбtб/Ctв = dбtб/tв,
где dб — плотность белкового раствора, tб и tв — время вытекания соответственно белкового раствора и воды. Относительная вязкость ηотн не зависит от постоянной С, которая является функцией диаметра капилляра.
Для случая очень разведенных суспензий шарообразных частиц Эйнштейн дал следующую формулу:
η = η0(1+2,5Nv/V), (4)
где N — число взвешенных частиц, v — объем каждой частицы, V — общий объем раствора. Если мы знаем число белковых молекул N, мы можем рассчитать объем, занимаемый каждой частицей, и таким путем определить, в какой степени она гидратирована. С другой стороны, если известна гидратация, мы можем рассчитать по формуле (4) число молекул N и вес частицы, который равен общему весу белка, деленному на N. Этим методом были получены величины гидратации для яичного альбумина, гемоглобина и других белков с шарообразными молекулами, хорошо совпадающие с величинами, полученными другими методами [41]. Большинство белков не обладает, однако, шарообразной формой молекулы, в связи с чем применимость этого метода очень ограничена.
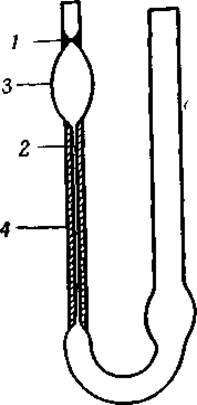
Фиг. 7. Вискозиметр Оствальда.
1 и 2 — два положения мениска; 3 — пипетка; 4 — капилляр.
Поскольку вязкость ηбелкового раствора всегда выше η0 — вязкости воды, относительная вязкость ηотн = η/η0 будет всегда больше единицы. Разница между этой величиной и единицей (ηотн —1) называется удельной вязкостью — ηуд. Согласно Штаудингеру [42], удельная вязкость растворов нитевидных макромолекул прямо пропорциональна концентрации и молекулярному весу растворенных макромолекул. В равенстве
ηуд = КсМ
К — постоянная для данного гомологичного ряда молекулярных цепочек одного и того же структурного образца, но различной длины, с — концентрация, а М — молекулярный вес.
Когда молекулярные цепочки находятся в растворенном состоянии, они только в очень редких случаях имеют форму вполне растянутой нити. В силу свободного вращения вокруг валентных связей, нити будут непрерывно сгибаться и разгибаться и в разные моменты времени будут принимать различные пространственные формы (фиг. 8).
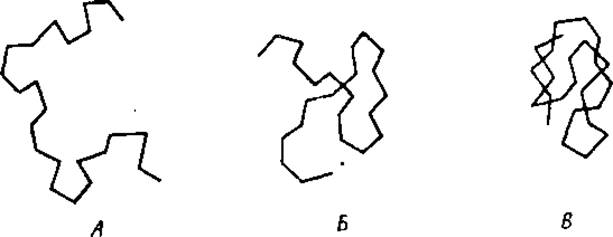
Фиг. 8. А, Б и В — различные конфигурации нитевидной макромолекулы.
Исходя из статистических соображений [43], следует считать среднюю длину нитевидной молекулы, т. е. расстояние между двумя концами нити, пропорциональной L, где L — длина цепочки полностью растянутой молекулы. Поскольку М пропорционально L, средняя длина нитевидной молекулы пропорциональна также М.
Вязкость раствора зависит не только от средней длины цепочки, но также и от того сопротивления, которое нитевидная молекула оказывает воздействиям, направленным на изменение ее пространственной конфигурации. С целью учета этих факторов величина М в уравнении Штаудингера заменяется на ее степенную функцию Ма причем а принимает значения от 0,5 до 1,5 [44, 45].
Когда измерения вязкости раствора высокомолекулярных веществ проводят при разных концентрациях, то получаются различные величины для ηотн и ηуд. Если начертить кривую изменения удельной вязкости в зависимости от концентрации раствора и экстраполировать ее до с = 0, то может быть определена так называемая внутренняя вязкость [η] молекулы. Она равна [46—48]
![]()
Измерения вязкости позволяют определить молекулярный вес таких нитевидных молекул, как молекулы каучука или эфиров целлюлозы; при определении же молекулярных весов белков положение осложняется электростатическим взаимодействием анионных и катионных боковых цепей белка и их влиянием на молекулы воды. В связи с этим вязкость белковых растворов зависит от pH раствора. Электростатическое действие ионизированных групп может быть уменьшено добавлением солей; вязкость полиэлектролитов уменьшается добавлением хлористого натрия [49, 50]. Из сказанного ясно, что определение вязкости белковых растворов само по себе может быть лишь с трудом применено для установления молекулярного веса и формы белковых молекул; этот метод, однако, может дать очень ценные результаты для изучения названных свойств белковых молекул при сочетании его с другими методами. Так, путем сочетания результатов вискозиметрии и измерений диффузии были получены следующие величины молекулярных весов: для яичного альбумина 40 500, для лактоглобулина 41 500, сывороточного альбумина 67 100, сывороточного глобулина 150 000—200 000, амандина (из миндаля) 330 000, тироглобулина 676 000, гемоцианина спрута 2 780 000 [51, 52]. Молекулярный вес вируса табачной мозаики был найден равным 63 200 000 и 42 600 000; размеры частиц вируса, в прекрасном соответствии с результатами диффузионных измерений [54], составили 11,5∙725 и 12,3∙430 mμ [53].
Если палочковидные частицы в растворе очень длинны и обладают достаточной жесткостью, наблюдается явление тиксотропии [55]. Как известно, это явление характеризуется образованием при продолжительном стоянии раствора геля, который при встряхивании раствора вновь способен разжижаться. Тиксотропия наблюдается в гелях сократимого мышечного белка — миозина.