Химия и биология белков - Ф. Гауровитц 1953
Белки с ферментативными свойствами
Кинетика ферментативных реакций
Напомним, что скорость реакций типа А → В + С зависит от [А], концентрации вещества А, и что скорость обратной реакции B + C → A зависит от [В] ∙ [С], произведения концентраций продуктов реакции. В состоянии равновесия В + С ⇄ А скорость прямой реакции равна скорости обратной реакции. Следовательно, мы можем написать:
![]()
Подобные рассуждения приложимы также к реакции образования фермент-субстратного комплекса. Если через Е обозначить молекулу фермента, а через S — молекулу субстрата, то образование фермент-субстратного комплекса можно представить следующим уравнением:
Е + S → ES.
Фермент-субстратный комплекс ES неустойчив. Он либо претерпевает обратную реакцию, ES → Е + S, распадаясь на свои исходные компоненты, либо расщепляется, согласно уравнению ES → Е + Р, где Р — продукт реакции. Скорость катализируемой реакции зависит главным образом от [ES], концентрации фермент-субстратного комплекса. По аналогии с формулой, приведенной выше для постоянной равновесия, мы можем и в этом случае написать:
![]()
где К — постоянная равновесия обратимой реакции Е + S ⇄ ES. Эта реакция, однако, никогда не бывает обратимой вследствие того, что продукт реакции ES распадается на свободный фермент Е и на продукты реакции Р, согласно уравнению ES → Е + Р. Скорость этой реакции пропорциональна концентрации ES, поэтому мы можем написать, что v1 = k3 [ES], где vp — скорость распада фермент-субстратного комплекса. Так как фермент-субстратный комплекс ES может распадаться либо на Е + S, либо на Е + Р, то должно возникнуть устойчивое состояние [34], постоянная равновесия которого будет равна:
![]()
Как правило, вследствие неустойчивости фермент-субстратного комплекса ES мы не можем определить ни концентрацию ES, ни концентрацию Е. Если мы обозначим через Еоб общее количество фермента, то общая концентрация фермента [Еоб] будет равна сумме концентраций [Е] и [ES]. Тогда концентрация свободного фермента [Е] будет равна [Eоб] — [ES], Подставляя это выражение в приведенную выше формулу (16), получаем:
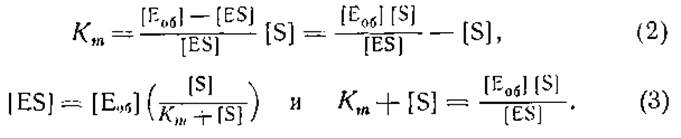
Согласно Михаэлису и Ментену [35], скорость ферментативной реакции пропорциональна [ES], концентрации фермент-субстратного комплекса. Как показывает последнее уравнение, концентрация фермент-субстратного комплекса, в свою очередь, пропорциональна [Еоб], общей концентрации фермента. Действительно, было найдено, что скорость большинства ферментативных реакций пропорциональна общей концентрации фермента.
Постоянная Кm носит название постоянной Михаэлиса. Если Кm = [S], то [ES] = [Еоб]/2, т. е., другими словами, скорость реакции равна половине максимальной скорости реакции, протекающей в присутствии большого избытка субстрата, когда [ES] [Eoб]. Это уравнение используется для определения Кm путем измерения скорости реакции при различных концентрациях субстрата. Постоянная Михаэлиса (Кm) соответствует такой концентрации субстрата S, при которой скорость реакции равна половине максимальной величины.
Из уравнения (3) следует, что [ES] зависит от Кm и от [S]. Если в состоянии равновесия [ES] будет бесконечно малой величиной по сравнению с [S] и с [Еoб], то скорость реакции будет зависеть только от [S], В этом случае при низких концентрациях субстрата эта реакция будет протекать по типу реакций первого порядка. Если же практически все количество фермента окажется связанным с субстратом в виде ES и если концентрация субстрата будет достаточно высока, то концентрация фермент-субстратного комплекса не будет меняться и скорость такой реакции окажется постоянной. В этом случае мы имеем дело с реакцией нулевого порядка [36]. Большинство ферментативных реакций не являются, строго говоря, ни реакциями первого, ни реакциями нулевого порядка, а протекают согласно некоему промежуточному порядку [34, 36, 37]. Это зависит отчасти от уменьшения концентрации субстрата в течение реакции, а отчасти от образования различных типов фермент-субстратных соединений. Так каталаза и пероксидаза, как уже указывалось выше, образуют зеленые и красные комплексы с субстратом, причем скорости распада зеленого и красного комплексов различны [32, 33]. Дальнейшие усложнения возникают вследствие соединения фермент-субстратных комплексов с водородными ионами [38] или с другими ионами или молекулами. Так, например, скорость гидролиза яичного альбумина пепсином зависит от концентрации водородных ионов раствора; реактивным промежуточным соединением является в этом случае не ES, a H+ES [38]. Если в образовании фермент-субстратного соединения участвуют ионы, то скорость катализируемой реакции зависит от диэлектрической постоянной растворителя; известно, что органические растворители, например метиловый или этиловый спирт, уменьшают диэлектрическую постоянную раствора и степень ионизации, вследствие чего уменьшается скорость катализируемой реакции [39].
Все предыдущие рассуждения основаны на том предположении, что скорость ферментативных реакций зависит от [ES], концентрации фермент-субстратного комплекса. Это предположение, однако, не совсем справедливо. Мы должны сделать дополнительное предположение, состоящее в том, что молекула ES требует определенного активирования, прежде чем она подвергнется распаду на фермент и на продукты реакции [34, 38j. Обозначим активированный фермент-субстратный комплекс через ES*. Тогда катализируемая реакция будет протекать через следующие фазы:
![]()
Если раствор содержит вещества, способные соединяться с ферментом, то между этими веществами и субстратом возникнет конкуренция за соединение с ферментом. Поэтому эти вещества будут действовать как ингибиторы. Для изучения кинетики ферментативных реакций в присутствии ингибиторов служат те же расчеты, какими мы пользовались при изучении кинетики реакции образования фермент-субстратного комплекса [40]. Напомним, что ферментативный гидролиз сахарозы инвертазой тормозится одним из продуктов реакции, а именно: фруктозой (см. стр. 281), которая в этом случае действует как ингибитор.
Различные ингибиторы реакции образования фермент-субстратного соединения (например, ионы, растворители, продукты реакции и др.) часто вызывают отклонение скорости ферментативной реакции от теоретической величины, вычисленной из уравнения(3).