ОСНОВЫ БИОХИМИИ ЛЕНИНДЖЕРА - ТОМ 2. БИОЭНЕРГЕТИКА И МЕТАБОЛИЗМ - 2014
ЧАСТЬ II. БИОЭНЕРГЕТИКА И МЕТАБОЛИЗМ
Благодаря изоморфизму энтропии и информации можно установить взаимосвязи между двумя формами энергии: энергией совершать действие и энергией направлять действие, которое совершается.
Франсуа Жакоб, La logique du vivant: une hitoire de I'heredite (Логика жизни: история наследственности), 1970
13. ОСНОВЫ БИОЭНЕРГЕТИКИ. ТИПЫ ХИМИЧЕСКИХ РЕАКЦИЙ
Живые клетки и организмы должны осуществлять процессы поддержания жизни, роста и размножения. Способность извлекать и преобразовывать энергию, которая расходуется на биологические процессы, является фундаментальным свойством всех живых организмов. Эта свойство было приобретено на ранней стадии клеточной эволюции. В современных организмах совершается множество разнообразных преобразований энергии, превращений одной формы энергии в другую. Живые организмы используют химическую энергию клеточных «топливных» молекул для синтеза сложных высокоупорядоченных макромолекул из простых молекул-предшественников. Они также превращают химическую энергию клеточного «топлива» в градиенты концентраций и градиенты электрических потенциалов, в движение и тепло. Немногие организмы, такие как светляки и некоторые глубоководные морские рыбы, способны излучать свет. Фотосинтезирующие организмы преобразуют световую энергию в другие формы энергии.
Антуан Лавуазье, 1743-1794

Химические механизмы, которые лежат в основе биологических преобразований энергии, в течение столетий зачаровывали биологов и бросали им вызов. Французский химик Антуан Лавуазье заметил, что животные каким-то образом превращают химическое «топливо», т. е. вещества из пищи, в тепло, и сделал вывод, что дыхание — жизненно важный процесс.
...в общем, дыхание не что иное, как медленное горение углерода и водорода, которое очень похоже на процесс, происходящий в керосиновой лампе или свече. С этой точки зрения животные, которые дышат, являются настоящими топливными котлами, которые сжигают и пожирают сами себя. Можно сказать, что эта аналогия между горением и дыханием не избежала внимания поэтов — правильнее, философов древности. Этот огонь, украденный с небес, этот факел Прометея не только идея, рожденная в головах инженеров и поэтов, он является верным описанием процессов, происходящих в природе, по крайней мере, в случае животных, которые дышат. Поэтому, следуя античным творениям, можно и нам пофилософствовать, сказав, что факел жизни зажигается в тот момент, как только младенец начинает дышать, и он не гаснет до тех пор, пока не наступает смерть*
* Из мемуаров Армана Сегена и Антуана Лавуазье, датированных 1789 г.; цитировано по книге [Lavoiser А. (1862) Oeuvres de Lavoisier, Imprimerie Imperiale, Paris].
В XX в. человечество достигло начального понимания большинства химических процессов «факела жизни». Превращения энергии в биологических системах подчиняются тем же физическим законам, которые управляют и всеми другими природными процессами. Поэтому студентам-биохимикам очень важно понять эти законы, а также то, как эти законы применимы к потоку энергии в биосфере.
В этой главе мы сначала обсудим законы термодинамики и количественные соотношения между свободной энергией, энтальпией и энтропией. Далее рассмотрим типы происходящих в живых клетках основных биохимических реакций, которые необходимы для использования, хранения, передачи и высвобождения энергии, воспринимаемой организмом из окружающей среды. Затем мы подробнее остановимся на тех реакциях, которые играют особую роль в биологических процессах энергетического обмена, в частности на реакциях с участием АТР. И наконец, перейдем к рассмотрению важных окислительно-восстановительных реакций в живых клетках, энергетических закономерностей переноса электронов в биологических системах, а также тех переносчиков электронов, которые наиболее часто работают в этих процессах в качестве кофакторов.
13.1. Биоэнергетика и термодинамика
Биоэнергетика изучает количественные стороны преобразований энергии из одной формы в другую, которые происходят в живых клетках, а также химические процессы, лежащие в основе этих преобразований. Хотя законы термодинамики уже обсуждались в предыдущих главах, а возможно, хорошо были изучены вами ранее, здесь будет весьма полезно в общих чертах вспомнить некоторые количественные аспекты.
Преобразования энергии в биологических системах подчиняются законам термодинамики
Многочисленные количественные исследования по взаимопревращению различных форм энергии, выполненные физиками и химиками, позволили в XIX в. сформулировать два основных закона термодинамики. Первый закон — это закон сохранения энергии: при любом физическом или химическом изменении общее количество энергии во вселенной остается постоянным; энергия может переходить из одной формы в другую или может перераспределиться, но не может исчезнуть. Второй закон термодинамики о том, что все процессы во вселенной стремятся к увеличению беспорядка (дезорганизации): в результате любых естественных процессов энтропия вселенной возрастает.

Живые организмы — это некая совокупность молекул, однако совокупность гораздо более высокоорганизованная, чем окружающие их вещества. Организмы способны создавать и поддерживать свойственную им упорядоченность, что, казалось бы, противоречит второму закону термодинамики. Однако на самом деле живые организмы тоже подчиняются этому закону и действуют строго в его рамках. Прежде чем начать обсуждение второго закона термодинамики в приложении к биологическим системам, следует дать определение этим системам и ввести такое понятие, как окружающая среда.
Под реакционной системой понимают совокупность веществ, которые подвергаются данному химическому или физическому процессу. Такой системой может быть организм, клетка или два реагирующих друг с другом соединения. Совокупность реакционной системы и окружающей среды составляет вселенную. В лаборатории некоторые химические или физические процессы могут протекать в изолированных или в закрытых системах, не способных к обмену веществ и энергии с окружающей средой. Однако живые клетки и организмы являются открытыми системами, которые обмениваются и веществами, и энергией с окружающей средой. Живые системы никогда не приходят к равновесию с окружающей средой. Постоянные взаимодействия между системой и окружающей средой объясняют, каким образом организмы могут поддерживать внутреннюю упорядоченность и при этом действовать в рамках второго закона термодинамики.
В гл. 1 (т. 1, с. 22) мы дали определение трем количественным термодинамическим функциям, с помощью которых можно выразить энергетические изменения, происходящие в химической реакции:
Свободная энергия Гиббса G — это та часть энергии, которая способна производить работу в реакции, протекающей при постоянной температуре и постоянном давлении. В тех случаях, когда реакция протекает с высвобождением свободной энергии (т. е. изменения в системе происходят с уменьшением свободной энергии), изменение свободной энергии ∆G — отрицательная величина, и такая реакция называется экзергонической. В эндергонических реакциях система приобретает (повышает) свободную энергию и ∆G> 0.
Энтальпия Н — это так называемое «теплосодержание» реакционной системы. Она отражает количество и природу химических связей в веществах, вступающих в реакцию, и в веществах — продуктах реакции. Химическая реакция, при которой происходит выделение тепла, называется экзотермической. Если энтальпия образования Hобр продуктов реакции меньше, чем для веществ, вступающих в реакцию, ∆Н <0. Реакционные системы, которые получают тепло от окружающей среды, называются эндотермическими: для них ∆Н — положительная величина.
Энтропия S — мера хаотичности (или неупорядоченности) системы (см. доп. 1-3). Когда продукты реакции менее сложные и более неупорядоченные, чем исходные вещества, считается, что реакция протекает с увеличением энтропии.
Единицы измерения ∆G и ∆Н — Дж/моль (джоуль на моль) и кал/моль (калории на моль). Напомним, 1 кал = 4,184 Дж. Единицы энтропии S — ДжДмоль • К) (джоуль на моль и на кельвин) (табл. 13-1).
Таблица 13-1. Некоторые физические постоянные и размерности некоторых термодинамических параметров
Константа Больцмана, к = 1,381 • 10-23 Дж/К
Число Авогадро, N = 6,022 • 1023 моль-1
Константа Фарадея, J = 96 480 Дж/(В • моль)
Газовая постоянная, R = 8,315 Дж (моль • К) (= 1,987 кал (моль • К))
Размерность ∆G и ∆Н — Дж/моль (или кал/моль)
Размерность ∆S — Дж (моль • К) (или кал/(моль • К)) 1 кал = 4,184 Дж
Размерность абсолютной температуры Т — К (кельвины) 25 °С = 298 К
При 25 °С RТ = 2,479 кДж/моль (= 0,592 ккал/моль)
В условиях, характерных для биологических систем (постоянная температура и давление), изменения свободной энергии, энтальпии и энтропии связаны количественно друг с другом следующим уравнением:
∆G = ∆Н — T∆S (13-1)
где ∆G — изменение свободной энергии реакционной системы, ∆Н — изменение энтальпии реакционной системы, Т — температура (в кельвинах, К) и ∆S — изменение энтропии системы. Условимся, что ∆S >0, когда энтропия увеличивается, и, как отмечалось выше, ∆Н <0, когда реакционная система отдает тепло окружающей среде. Для самопроизвольно (спонтанно) протекающих реакций и природных процессов всегда ∆G <0.
По второму закону термодинамики при химических реакциях или физических процессах энтропия вселенной увеличивается. Из этого закона, однако, не следует, что возрастание энтропии должно происходить обязательно в самой реакционной системе. Внутриклеточная упорядоченность, которая создается в процессе роста и деления клеток, более чем компенсируется возникающей при этом неупорядоченностью в окружающей среде. Коротко говоря, живые организмы сохраняют внутреннюю упорядоченность, получая из окружающей среды свободную энергию в виде питательных веществ или солнечного света и возвращая в нее такое же количество энергии в виде тепла и энтропии.
Клеткам необходимы источники свободной энергии
Клетки — изотермические системы, они функционируют при постоянной температуре (а также при постоянном давлении). Тепло (нагревание) не может служить источником энергии для клеток, поскольку тепло способно производить работу лишь в том случае, когда оно переходит от более нагретого тела к более холодному или из области с более высокой температурой в область с более низкой температурой. Клетки могут и должны использовать свободную энергию Гиббса G, которая связана с прочностью химических связей между атомами, определяет состояние равновесия и направление химических реакций; это та теоретически возможная химическая энергия системы, которая может быть превращена в работу, т. е. выделена во вселенную в виде тепла и энтропии при протекании химической реакции при постоянной
температуре и постоянном давлении. Гетеротрофные клетки извлекают необходимую свободную энергию из молекул питательных веществ, а фотосинтезирующие клетки поглощают энергию солнечного света. И те, и другие переводят свободную энергию в АТР и другие «энергетические» соединения, которые способны запасать энергию для выполнения работы (биологических процессов) в условиях постоянной температуры.
Изменение стандартной свободной энергии непосредственно связано с константой равновесия
Состав реакционной системы (смесь веществ, вступающих в реакции, и продуктов реакции) меняется до тех пор, пока не устанавливается равновесие. По достижении равновесия концентрации реагирующих веществ и продуктов реакции не меняются, скорости прямой и обратной реакций становятся равными и дальнейшие изменения в системе прекращаются. Концентрации реагирующих веществ и продуктов реакции в состоянии равновесия определяют константу равновесия Кеq (т. 1, с. 24). Запишем для обобщенной реакции
аА + bВ ⇄ cC+dD
где а, b, с и d — число молекул А, В, С и D, константу равновесия
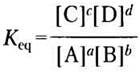 (13-2)
(13-2)
где [А], [В], [С] и [D] — молярные концентрации веществ в состоянии равновесия.
Неравновесная реакционная система всегда самопроизвольно стремится к установлению равновесного состояния при заданных условиях (концентрация, температура, давление); при этом происходит изменение свободной энергии реакции ∆G. При стандартных условиях, т. е. при температуре Т = 298 К = 25 °С, исходных концентрациях всех компонентов реакции 1 моль/л (или М), или для газообразных веществ парциальном давлении 101,3 кПа (килопаскаль) = 1 атм, движущая сила системы к состоянию равновесия определяется изменением стандартной свободной энергии ∆G°. Стандартными условиями для реакций с участием ионов водорода является [H+] = 1 М, или pH 0.
Большинство биохимических реакций происходит в разбавленных буферных растворах при pH ≈ 7. При этом и pH, и концентрацию воды (для чистой воды [Н2О] = 55,5 М) можно считать постоянными. Для удобства расчетов в качестве стандартных условий для биохимических процессов приняты следующие: концентрация водородных ионов 10-7М (pH 7), концентрация воды 55,5 М и концентрация Mg2+ 1 мМ (для реакций, протекающих с участием ионов Mg2+, включая большинство реакций, где взаимодействует АТР).
Ключевые договоренности
Для удобства в качестве стандартного состояния (стандартных условий) биохимических систем выбраны условия, отличные от тех, что приняты в химии и физике. А именно, в биохимии стандартное состояние соответствует [Н+] = 10-7 М (pH 7) и [Н2О] = 55,5 М. Для реакций с участием ионов Mg2+ (к которым относятся многие реакции с участием АТР) концентрация Mg2+ в растворе обычно считается постоянной и равной 1 мМ. ■
Физические параметры, относящиеся к биохимическому стандартному состоянию, называются стандартными приведенными параметрами и пишутся со штрихом (например, ∆G'° и К′eq) для того, чтобы отличать их от неприведенных параметров, используемых химиками и физиками. Заметим, что в других учебниках биохимии чаще используется обозначение ∆G°' (а не ∆G'°, как мы ввели выше). Параметр ∆G'° рекомендован Международным союзом химиков и биохимиков с целью подчеркнуть, что неприведенный параметр G' — это критерий равновесия. Для простоты здесь и далее будем называть эти приведенные параметры стандартными изменениями свободной энергии.
Ключевые договоренности
Согласно другой договоренности, если Н2O, Н+ и/или Mg2+ выступают в качестве исходных веществ или продуктов реакции, их концентрации не включаются в уравнения, такие как (13-2), а вместо этого входят в константы К'eq и ∆G'°. ■
Итак, для реакции характерна константа равновесия К'еq, отсюда и ∆G' — это характеристический параметр реакции. Как мы отмечали в гл. 6, К'eq и ∆G'° связаны простым соотношением:
∆G'° = -RT In K'eq (13-3)
Это просто один из возможных способов расчета константы равновесия реакции через изменение стандартной свободной энергии химической реакции. В табл. 13-2 приведены значения ∆G'° и K'eq. Если К'еq = 1,0, то ∆G'° = 0,0 (так как In 1,0 = 0). Если К'eq> 1,0, то ∆G'° <0. Если же К'еq <1,0, ∆G'°> 0. Поскольку зависимость ∆G'° от K'eqлогарифмическая, относительно небольшие изменения ∆G'° приводят к сильным изменениям К’eq.
Таблица 13-2. Константы равновесия и изменения стандартной свободной энергии реакции
∆G'° |
||
K'eq |
кДж/моль |
ккал/моль* |
103 |
-17,1 |
-4,1 |
102 |
-11,4 |
-2,7 |
101 |
-5,7 |
-1,4 |
1 |
0,0 |
0,0 |
10-1 |
5.7 |
1,4 |
10-2 |
11,4 |
2,7 |
10-3 |
17,1 |
4,1 |
10-4 |
22,8 |
5,5 |
10-5 |
28,5 |
6,8 |
10-6 |
34,2 |
8,2 |
* В СИ размерность энергии — джоуль (и килоджоуль); сокращенно Дж (и кДж). Однако биохимики чаще всего приводят ∆G'° в ккал/моль (килокалория на моль). 1 кДж = 4,184 ккал.
Полезно также определить изменение свободной энергии и другим путем. ∆G'° — это разность между свободной энергией продуктов реакции и свободной энергией исходных веществ. Когда ∆G’° <0, свободная энергия образования Gобр (продуктов реакции) <Goбp (реагентов); такая реакция при стандартных условиях происходит самопроизвольно (спонтанно), поскольку все химические реакции стремятся идти в направлении, соответствующем уменьшению свободной энергии системы. Если ∆G'°> 0, то Goбp (продуктов реакции)> Goбp (реагентов). При концентрациях исходных компонентов 1,0 М (стандартные условия) такая реакция идет в обратном направлении. В табл. 13-3 обобщены эти положения.
Таблица 13-3. К'еq, ∆G'° и направление химических реакций при стандартных условиях
К'еq |
∆G'° |
При начальной концентрации всех веществ 1 М |
>1,0 |
<0 |
Прямая реакция |
1,0 |
0 |
Равновесное состояние |
<1,0 |
>0 |
Обратная реакция |
Пример 13-1. Расчет ∆G'°
Найдите изменение свободной энергии реакции, катализируемой ферментом фосфоглюкомутазой:
Глюкозо-1-фосфат ⇄ глюкозо-6-фосфат
В начале реакции концентрация глюкозо-1- фосфата составляла 20 мМ, а глюкозо-6-фосфат в реакционной среде отсутствовал; в равновесной смеси при 25 °С и pH 7,0 содержится 1,0 мМ глюкозо-1-фосфата и 19 мМ глюкозо-6-фосфата. Потерей или увеличением свободной энергии сопровождается реакция, идущая в направлении образования глюкозо-6-фосфата?
Решение. Следует рассчитать константу равновесия:
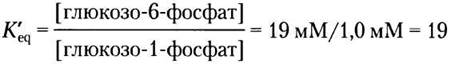
Теперь можно найти стандартное изменение свободной энергии:
∆G'° = -RT In К'еq = - (8,315 ДжДмоль • К) (298 К) (In 19) = -7,3 кДж/моль
∆G'° <0, т. е. превращение глюкозо-1-фосфата в глюкозо-6-фосфат сопровождается уменьшением (потерей, высвобождением) свободной энергии. В обратной реакции изменение свободной энергии равно по величине, но противоположно по знаку, т. е. ∆G'° >0.
В табл. 13-4 приведены численные значения изменений стандартной свободной энергии некоторых важных химических реакций. Отметим, что гидролиз простых эфиров, амидов пептидов и гликозидов, как и внутримолекулярные перегруппировки и элиминирование, сопровождаются небольшим изменением стандартной свободной энергии, в то время как при гидролизе ангидридов кислот происходит значительное уменьшение стандартной свободной энергии. Полное окисление органических веществ, таких как глюкоза или пальмитиновая кислота, до СO2 и Н2O, протекающее в клетках многоступенчато, приводит к очень большому уменьшению стандартной свободной энергии. Данные, приведенные в табл. 13-4, относятся к стандартным условиям. Параметры реакций, происходящих в клетке, можно получить, приведя величины в стандартных условиях к реальным условиям (в клетке).
Таблица 13-4. Изменение стандартной свободной энергии в некоторых химических реакциях при pH 7,0 и 25 °С (298 К)
Реакция |
∆G'° кДж/моль |
ккал/моль |
|||
Гидролиз Кислотный гидролиз Уксусный ангидрид + Н2O —> 2 ацетата |
-91,1 |
-21,8 |
|||
АТР + Н2O —> ADP + Рi |
-30,5 |
-7,3 |
|||
ATP + Н2O —> АМР + PPi |
-45,6 |
-10,9 |
|||
PPi + Н2O —> 2Рi |
-19,2 |
-4,6 |
|||
UDP-глюкоза + Н2O —> UMP + глюкозо-1-фосфат |
-43,0 |
-10,3 |
|||
Гидролиз эфиров Этилацетат + Н2O —> этанол + ацетат |
-19,6 |
-4,7 |
|||
Глюкозо-6-фосфат + Н2O —> глюкоза + Рi |
-13.8 |
-3.3 |
|||
Гидролиз амидов и пептидов Глутамин + Н2O —> глутамат + NH4+ |
-14.2 |
-3.4 |
|||
Глицилглицин + Н2O —> 2 глицина |
-9,2 |
-2,2 |
|||
Гидролиз гликозидов Мальтоза + Н2O —> 2 глюкозы |
-15,5 |
-3,7 |
|||
Лактоза + Н2O —> глюкоза + галактоза |
-15.9 |
-3,8 |
|||
Внутримолекулярные перегруппировки Глюкозо-1-фосфат —> глюкозо-6-фосфат |
-7.3 |
-1.7 |
|||
Фруктозо-6-фосфат —> глюкозо-6-фосфат |
-1,7 |
-0,4 |
|||
Отщепление воды Малат —> фумарат + Н2O |
3,1 |
0,8 |
|||
Окисление молекулярным кислородом Глюкоза + 6O2 —> 6СO2 + 6Н2O |
-2,840 |
-686 |
|||
Пальмитат + 23O2 —> 16СO2 + 16Н2O |
-9,770 |
-2,338 |
|||
Изменения свободной энергии в реальных системах зависят от концентраций исходных веществ и продуктов реакции
Мы должны четко уяснить, что изменение свободной энергии ∆G и изменение стандартной свободной энергии ∆G′° численно различаются. Каждая химическая реакция характеризуется определенным изменением стандартной свободной энергии, которое может быть положительным, отрицательным или равным нулю в зависимости от константы равновесия данной реакции. По изменению стандартной свободной энергии можно судить о том, в каком направлении протекает данная реакция и как далека она от равновесия при исходных концентрациях всех компонентов 1,0 М, pH 7,0, температуре 25 °С и давлении 101,3 кПа. Таким образом, ∆G′° — характеристический параметр (константа) данной реакции. Однако в реальных условиях изменение свободной энергии ∆G зависит от концентраций исходных веществ и продуктов реакции, а также от изменения температуры по ходу реакции. Реальные условия могут не совпадать со стандартными. Более того, ∆G любой реакции, спонтанно стремящейся к равновесию, всегда отрицательная величина, и по мере протекания реакции ∆G увеличивается, стремясь в пределе к нулю. В момент установления равновесия ∆G = 0 — в данной реакции больше не может быть совершено никакой работы.
Для любой реакции аА + bВ ⇄ сС + dD ∆G и ∆G′° связаны уравнением
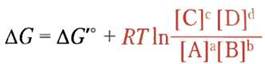 (13-4)
(13-4)
в котором параметры, выделенные красным, преобладающие в данной системе. Концентрации в уравнении 13-4 принято называть действующими массами, а отношение [С]с[D]d|/[А]а[В]b выражает закон действующих масс Q. В качестве примера давайте предположим, что реакция А + В ⇄ С + D протекает при стандартных условиях температуры (25 °С) и давления (101,3 кПа), но что концентрации [А], [В], [С] и [D] не равны между собой и ни одна из них не равна стандартной концентрации 1,0 М. Чтобы найти изменение свободной энергии ∆G реакции, протекающей слева направо, при этих нестандартных условиях, подставим численные значения концентраций компонентов А, В, С иD в уравнение 13-3. Параметры R, Т и ∆G′° относятся к стандартным условиям. ∆G <0 и по мере протекания реакции этот параметр стремится к нулю из-за того, что вещества А и В расходуются ([А] и [В] уменьшаются), а вещества С и D нарабатываются ([С] и [D] увеличиваются). Отметим, что в состоянии равновесия ∆G = 0 и уравнение 13-4 упрощается:
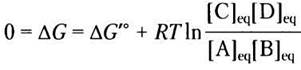
∆G′° = -RT In K'eq
т. е. мы снова получили уравнение 13-3, связывающее изменение стандартной свободной энергии и константу равновесия.
Критерий самопроизвольности реакции связан с ∆G, а не с ∆G′°. При ∆G° >0 реакция идет только при условии, что ∆G <0. Такое возможно, когда в уравнении 13-4 0 <RT In([продукты реакции]/[исходные вещества)) > ∆G′. Например, при немедленном удалении продуктов реакции отношение [продукты реакции]/[исходные вещества] « 1, так что RTIn [продукты реакции]/ [исходные вещества] <0 (большое отрицательное число). Величины ∆G и ∆G′° выражают максимальное количество свободной энергии, которое теоретически данная реакция может предоставить, т. е. количество энергии, которое могло быть реализовано, если бы имелся высокоэффективный механизм ее использования. Поскольку такого механизма нет (во время любого процесса, какая-то часть свободной энергии всегда теряется в виде энтропии), количество работы, выполненное за счет данной реакции при постоянной температуре и постоянном давлении, всегда меньше теоретически ожидаемого.
Другой важный момент заключается в том, что некоторые благоприятные в термодинамическом отношении реакции (а именно, реакции, для которых ∆G'° «0) происходят с недостаточно большой скоростью. Например, горение (реакция окисления) дров до СO2 и Н2O термодинамически очень выгодно. Однако дрова хранятся годами — горение начинается не самопроизвольно, поскольку энергия активации (см. рис. 6-2 и 6-3) реакции горения выше, чем доступная при комнатной температуре энергия. Если предоставить необходимую энергию активации (например, от зажженной спички), начнется процесс горения, превращающий дерево в более стабильные продукты СO2 и Н2O и высвобождающий энергию в виде тепла и света. Теплота, выделенная при этой экзотермической реакции, обеспечивает энергию активации для горения следующих порций дров, и таким образом процесс горения может продолжаться непрерывно.
В живых клетках химические реакции протекали бы чрезвычайно медленно, если бы там не было эффективных катализаторов — ферментов, которые вовсе не обеспечивают реакционную систему дополнительным теплом (энергией), а понижают энергию активации. Фермент «предлагает» альтернативный путь реакции с более низкой энергией активации, чем в случае некатализируемой реакции, для того чтобы энергия большинства молекул субстрата при комнатной температуре оказалась достаточной для преодоления энергетического барьера — энергии активации. Благодаря ферментативному катализу скорость реакции увеличивается во много раз. Изменение свободной энергии реакции не зависит от пути, по которому реакция протекает, а зависит только от природы и концентрации исходных веществ и конечных продуктов реакции. При ферментативном катализе не изменяется величина константы равновесия реакции; но под действием ферментов может увеличиваться и
действительно увеличивается скорости прямой и обратной реакций и процесс идет в термодинамически разрешенном направлении (знаком изменения свободной энергии).
Изменения стандартной свободной энергии аддитивны
Рассмотрим последовательные реакции А ⇄ В и В ⇄ С. Каждая реакция имеет собственную константу равновесия и характеризуется определенным изменением стандартной свободной энергии ∆G1'° и ∆G2'°. Поскольку эти две реакции протекают последовательно, компонент В можно исключить из обсуждения. Тогда рассмотрим суммарную реакцию А ⇄ С, которая характеризуется константой равновесия и, следовательно, изменением стандартной свободной энергии ∆G'°общ. Для последовательных химических реакций ∆G'° аддитивны. Для суммарной реакции А ⇄ С общее изменение стандартной свободной энергии ∆G'°общ равно сумме изменений стандартных свободных энергий ∆G1'° и ∆G2'° двух реакций: ∆G'°общ ⇄ ∆G1'° + ∆G2'°
(1) A —> В ∆G1'°
(2) B —> C ∆G2'°
Итого: А —> С ∆G1'° + ∆G2'°
Этот принцип биоэнергетики объясняет, как реакция (эндергоническая реакция), не выгодная термодинамически, может быть проведена в прямом направлении при сопряжении с высокоэкзергонической реакцией через общий промежуточный продукт. Например, у многих организмов синтез глюкозо-6-фосфата является первой стадией при усвоении глюкозы:
Глюкоза + Рi —> глюкозо-6-фосфат + Н2O
∆G'° = 13,8 кДж/моль
Для этой реакции ∆G'° >0, и при стандартных условиях реакция самопроизвольно не происходит в указанном направлении. Другой процесс в клетке — гидролиз АТР до ADPи Pi — наоборот высокоэкзергонический:
АТР +Н2O —> ADP + Pi
∆G'° = -30,5 кДж/моль
Эти две реакции связаны общими промежуточными продуктами Pi и Н2O и их можно представить как последовательные реакции:
(1) Глюкоза + Рi —> глюкозо-6-фосфат + Н2O
(2) АТР +Н2O —> ADP + Pi
Итого: АТР + глюкоза —> ADP + глюкозо-6-фосфат
Общее изменение стандартной свободной энергии можно получить как сумму ∆G'° отдельных реакций:
∆G'° = 13,8 кДж/моль + (-30,5 кДж/моль) = -16,7 кДж/моль
Суммарная реакция экзергоническая, и энергия, запасенная в АТР, используется для синтеза глюкозо-6-фосфата, хотя образование этого соединения из глюкозы и неорганического фосфата Pi — эндергонический процесс. Реальный путь образования глюкозо-6-фосфата в клетке путем переноса фосфатной группы от АТР отличается от приведенных выше реакций (1) и (2), но конечный результат получается тот же самый, что и при суммировании этих двух реакций. В термодинамических расчетах состояния системы в начале и конце процесса представлены этими веществами. А путь между начальным и конечным состояниями не важен.
Мы уже говорили о том, что ∆G'° — способ выражения константы равновесия реакции. Для реакции (1)
![]()
Заметим, что Н2O не входит в это выражение, поскольку концентрация воды (55,5 М) не изменяется в ходе реакции. Константа равновесия реакции гидролиза АТР равна
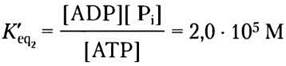
а константа равновесия двух сопряженных реакций
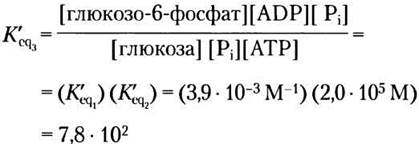
Здесь следует обратить внимание на важный момент, касающийся константы равновесия. Хотя ∆G'° двух реакций, из которых слагается третья, аддитивны, К'еq суммарной реакции равна произведению К’еq этих отдельных реакций. Говорят, что константы равновесия реакций мультипликативны. Благодаря сопряжению гидролиза АТР с синтезом глюкозо-6-фосфата К’eq увеличивается в 2,0 • 105 раза.
Эта стратегия, где при синтезе вторичных метаболитов и клеточных компонентов присутствует общий промежуточный продукт, встречается во всех живых клетках. Очевидно, что она работает только при условии постоянного наличия таких соединений, как АТР. В следующих главах мы обсудим некоторые из наиболее важных путей синтеза АТР.
Краткое содержание раздела 13.1. Биоэнергетика и термодинамика
■ Живые клетки постоянно выполняют работу. Для поддержания своих высокоорганизованных структур, синтеза клеточных компонентов и многих других процессов клеткам необходима энергия.
■ Биоэнергетика занимается количественным изучением превращений энергии в биологических системах. Биологические превращения энергии подчиняются законам термодинамики.
■ На ход любой химической реакции влияют два фактора: стремление к состоянию с наибольшей устойчивостью (прочностью) связей (характеризуется энтальпией Н) и стремление к наивысшей неупорядоченности системы (характеризуется энтропией S). Суммарной движущей силой реакции является изменение свободной энергии ∆G; этот термодинамический параметр учитывает общий эффект этих двух факторов: ∆G = ∆Н — T∆S.
■ Изменение стандартной свободной энергии — характеристический физико-химический параметр данной реакции; его можно рассчитать из константы равновесия: ∆G’° = - RTIn K’eq.
■ В реальной системе изменение свободной энергии ∆G не константа, а зависит от ∆G′° и от концентраций исходных веществ и продуктов реакции:
■ Когда ∆G «0, реакция протекает слева направо (т. е. в прямом направлении); когда ∆G «0, реакция стремится идти в обратном направлении; и когда ∆G = 0, система находится в состоянии равновесия.
■ Изменение свободной энергии реакции не зависит от пути протекания реакции. Изменение свободной энергии нескольких последовательных реакций (стадий) — аддитивный параметр; общее изменение свободной энергии суммарной химической реакции, которая является результатом последовательных реакций с общим промежуточным продуктом, равно сумме ∆G отдельных реакций.