Биохимия человека Том 1 - Марри Р. 1993
Структура и функции белков и ферментов
Ферменты: кинетика
Уравнение Михаэлиса-Ментен
Графическое определение константы Михаэлиса КМ
Концентрация субстрата, при которой скорость составляет половину максимальной, обозначается через КМ и называется константой Михаэлиса. Ее можно определить из графика зависимости г от [S] (рис. 8.14). Обратите внимание, что КМ имеет размерность молярной концентрации.
Когда [S] приближается к КМ, v становится весьма чувствительной к изменению [S]; в этой области фермент работает со скоростью, равной половине максимальной. Многие ферменты характеризуются такими значениями КМ, которые примерно соответствуют физиологическим концентрациям их субстратов.
Уравнение Михаэлиса—Ментен
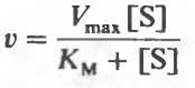
описывает поведение многих ферментов при изменении концентрации субстратов. Используя это уравнение, зависимость начальной скорости ферментативной реакции от [S] и КМ можно проиллюстрировать на следующих конкретных примерах.
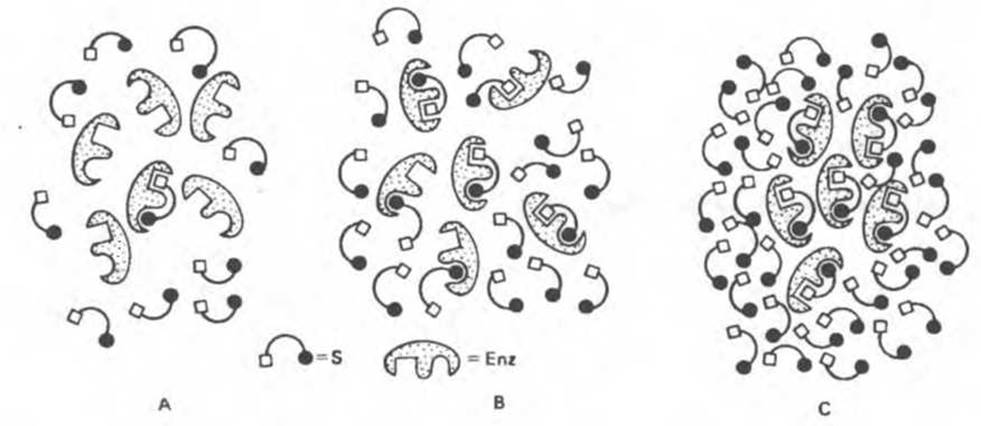
Рис. 8.15. Схема, поясняющая связывание субстрата ферментом при низкой (А) и высокой (С) концентрации субстрата, а также при концентрации субстрата, равной КМ (В). Состояния А, В и С отвечают точкам А, В, С на кривой, приведенной на рис. 8.14.
1. [S] много меньше КМ (точка Л на рис. 8.14 и 8.15). В этом случае величину [S] в знаменателе можно опустить, и он будет практически равен КМ. Отношение двух констант, Vmаx и КM, можно заменить новой константой К. Таким образом, имеем:
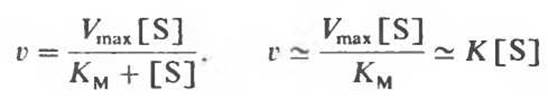
(≃ означает «примерно равно»).
Другими словами, когда концентрация субстрата значительно ниже той, при которой скорость реакции составляет половину максимальной (т. е. значительно меньше КM), начальная скорость v пропорциональна концентрации субстрата [S].
2. |S| много больше КM (точка С на рис. 8.14 и 8.15). В этом случае член КM в знаменателе можно опустить, т. е.
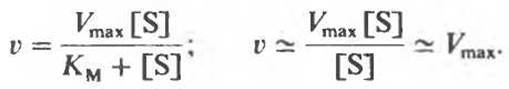
Это означает, что при концентрации субстрата [S], намного превышающей KM, начальная скорость v равна максимальной Vmax.
3. [S] = KМ (точка В на рис. 8.14 и 8.15).
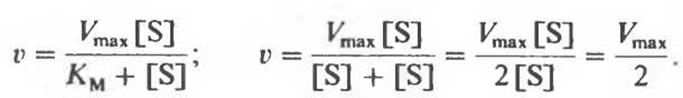
Это означает, что при концентрации субстрата, равной КM, начальная скорость реакции v составляет половину максимальной. Отсюда же следует способ оценки КM: надо экспериментально определить концентрацию субстрата, при которой начальная скорость равна половине максимальной.
Для многих ферментов определение Vmах (а значит, и КM) непосредственно из графика зависимости V от [S] оказывается затруднено. Для этого используют уравнение, обратное уравнению Михаэлиса—Ментен, т. е.
![]()
и представляют его правую часть в виде суммы двух слагаемых:
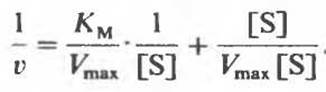
Отсюда, упростив, получаем
![]()
Итак, мы имеем уравнение прямой
у = ах + b,
где у = 1/v и x = 1/[S].
Если построить график зависимости у (т.е. 1 /v) от л: (т.е. 1 /[S]), то длина отрезка b, отсекаемого от оси у, будет равна 1/Vmах, а тангенс угла наклона а — KM/Vmax. Длину отрезка, отсекаемого от оси х (в области отрицательных значений), можно получить, приравняв у нулю. Тогда
![]()
График уравнения Михаэлиса—Ментен в обратных координатах называют графиком Лайнуивера—Бэрка (рис. 8.16). Используя его, КM можно найти либо из наклона прямой и длины отрезка, отсекаемого от оси у, либо из длины отрезка, отсекаемого в области отрицательных значений от оси х. Поскольку [S] имеет размерность молярной концентрации, КM тоже измеряется в молях на литр. Скорость v может быть выражена в любых единицах, поскольку КM не зависит от [Enz.]. График, построенный в обратных координатах, позволяет определить КM по относительно небольшому числу точек, именно поэтому он часто используется для нахождения КM.
Используя график Лайнуивера—Бэрка на практике для оценки Км, иногда сталкиваются с тем, что почти все точки оказываются в области низких концентраций субстрата. Это происходит в том случае, когда измерения проводят через равные интервалы [S]. Чтобы этого избежать, измерения следует проводить при таких значениях [S], которые соответствуют равным интервалам по шкале обратных величин.
Альтернативный подход к экспериментальной оценке Км и Vmах предложили Иди и Хофсти. Уравнение Михаэлиса — Ментен можно преобразовать к виду
![]()
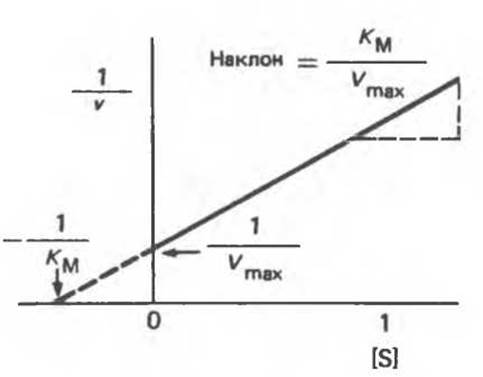
Рис. 8.16. Г рафик Лайнуивера — Бэрка в двойных обратных координатах (зависимость 1/vх от 1 /[S]), используемый для графического определения КM и Vmax.
Чтобы найти КM и Vmax, строят график зависимости v/[S] (ось у) от V (ось х). Тогда длина отрезка, отсекаемого от оси у, будет равна Vmах/КM, а отрезка, отсекаемого от оси x,— Vmax. Тангенс угла наклона равен — 1/КM.
Уравнения Лайнуивера—Бэрка и Иди — Хофсти весьма удобны в некоторых случаях, однако для строгого определения КM и Vmах требуется соответствующая статистическая обработка.
Оценки Км имеют практическую ценность. При концентрациях субстрата, в 100 раз превышающих КM фермент будет работать практически с максимальной скоростью, поэтому максимальная скорость (Vmax) будет отражать количество присутствующего активного фермента. Это немаловажное обстоятельство используют для оценки содержания фермента в препарате. Значение KM позволяет ориентироваться, какое количество субстрата следует добавить для определения Vmах. Графики, построенные в обратных координатах, находят широкое применение при оценке действия ингибиторов.
Соотношение между КM и Кd — константой диссоциации фермент-субстратного комплекса
Сродство фермента к субстрату равно величине, обратной константе диссоциации Кd комплекса Enz—S:
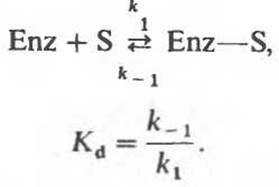
Иными словами, чем слабее выражена тенденция фермент-субстратного комплекса к диссоциации, тем выше сродство фермента к субстрату.
Мерой Kd может ориентировочно служить значение КM для данного фермента по отношению к его субстрату. Однако это возможно только в том случае, если справедливо допущение, использовавшееся при выводе уравнения Михаэлиса—Ментен. Оно состояло в том, что первая стадия ферментативной реакции
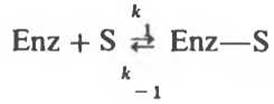
идет быстро и при этом всегда на этой стадии поддерживается равновесие. Другими словами, скорость диссоциации Enz—S на Enz + S намного выше,
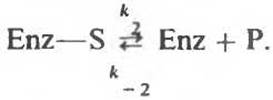
Из уравнения Михаэлиса—Ментен следует, что величина [S], при которой
![]()
равна
![]()
Но если
k-1 » k2,
то
k2 + k ≃ k-1
и
![]()
При этих условиях 1/КM = 1/КM и равно сродству фермента к субстрату. Если k2 + k-1≉ k-1, то 1/КM даст заниженную оценку сродства.