Биохимия - Химические реакции в живой клетке Том 2 - Д. Мецлер 1980
Ферменты: белковые катализаторы клеток
Основы ферментативной кинетики
Реакции с участием двух и большего числа субстратов
Ферменты часто катализируют реакции, протекающие с участием двух, трех и даже большего числа субстратов и приводящие к образованию двух, трех и большего числа продуктов. В одних случаях все молекулы субстрата должны быть одновременно связаны с активным центром фермента и располагаться таким образом, чтобы они могли реагировать в определенной последовательности. В других случаях фермент трансформирует молекулу А в продукт, что приводит к взаимодействию.
Присоединение двух молекул субстратов (А и В) к молекуле фермента с образованием комплекса ЕАВ может происходить как совершенно неупорядоченно, так и упорядоченно. При исследовании реальных ферментов встречаются обе ситуации. Для описания различных возможностей присоединения субстратов и отщепления продуктов широко используется метод, предложенный Клеландом. Например, схема
![]()
означает, что связывание А и В с ферментом происходит упорядоченно, образуется комплекс ЕАВ, который затем изомеризуется в комплекс EPQ. Последний можно рассматривать как результат присоединения продуктов Р и Q к ферменту. Константы скорости, расположенные на схеме слева от каждой вертикальной стрелки или выше горизонтальной, соответствуют прямой реакции, а константы, расположенные справа от вертикальных стрелок или ниже горизонтальных, — обратной. Скорость прямой реакции для ферментативного процесса с упорядоченным связыванием субстратов и упорядоченным отщеплением продуктов задается следующим выражением:
![]()
Выражение, обратное данному, имеет вид1)
![]()
Уравнения (6-35а) и (6-356) содержат следующие кинетические параметры: Vf— максимальную скорость прямой реакции, две константы Михаэлиса КМВ и КМА константу равновесия ЕедА, которая представляет собой константу обратимой диссоциации комплекса ЕА и равна отношению k2/k1. В общем случае кинетические константы k1—k10и параметры уравнения (6-35а), определяемые экспериментально (константы Михаэлиса, максимальные скорости и константы равновесия для двойных комплексов), не связаны явным образом. Однако отдельные кинетические константы удается найти из экспериментально измеряемых параметров.
Уравнение, идентичное (6-35а), можно записать и для скорости обратной реакции (vr), протекающей с участием молекул Р и Q. Уравнение для мгновенной скорости реакции в случае произвольной смеси всех четырех компонентов — А, В, Р и Q — т. е. уравнение для (vt—vr), имеет такой же вид.
Кинетические параметры, входящие в уравнение (6-35б), часто находят из экспериментальных данных, используя графики двойных обратных координат (рис. 6-5). Обратите внимание на то, что уравнение (6-35б) является линейным только в том случае, если либо концентрация субстрата А, либо концентрация субстрата В постоянна. Чтобы выполнить это условие, проводят серию экспериментов, в которых варьируют, например, концентрацию субстрата А, поддерживая концентрацию В постоянной. Затем фиксируют концентрацию субстрата А и варьируют концентрацию субстрата В. Каждая серия подобных экспериментов дает семейство прямых (рис. 6-5,А), для которых находят наклоны и отсекаемые на оси ординат отрезки. Далее строят зависимость наклонов и отсекаемых отрезков от обратной концентрации того субстрата, концентрация которого в каждой из серий экспериментов поддерживалась постоянной.
1) Другая часто применяющаяся (форма этого уравнения предложена Динлом [22]:
![]()
Суммарная концентрация фермента обычно равна vt/kt [см. уравнение (6-6)]. Из уравнения (6-35б) следует, что φ0—1/kt, причем для схемы (6-34) kt может быть приравнена в некоторых случаях константе kt.
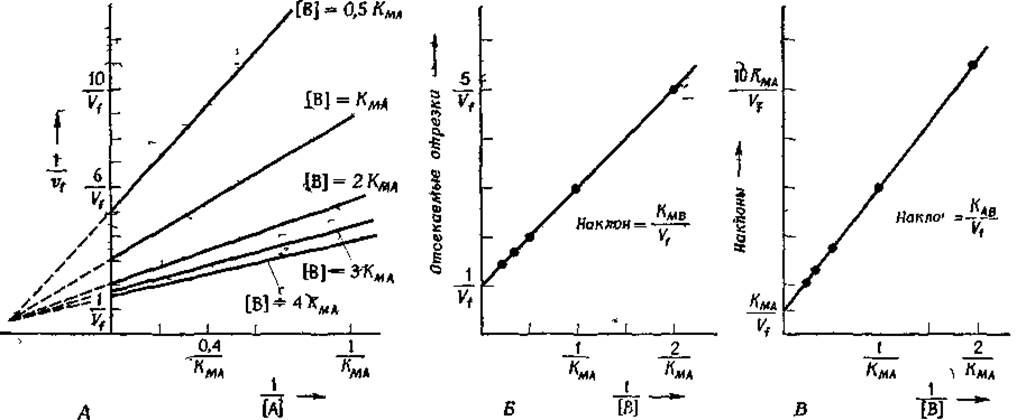
РИС. 6-5 Графики двойных обратных координат, используемые для анализа кинетики двухсубстратных ферментативных реакций. А Серия зависимостей 1/vt oт 1/[А] при различных фиксированных концентрациях второго субстрата (В). Б Вторичный график зависимости длины отрезка, отсекаемого на оси ординат прямыми в координатах {1/vt; 1/[А]}, от 1 /[В] В Вторичный график зависимости наклона первичных зависимостей, представленных на рис А, от 1/[B]. Все зависимости рассчитаны с помощью уравнения (6-35а) при следующих значениях параметров KMA=10-3 М, KMB = 2KMA, KAB = KeqAKMB = КMA/200, [А] = [В] = 1 М В качестве первичных графиков можно использовать также графики Эдн—Хофсти, т. е. графики зависимости vt/[A] от vt, построенные при постоянных концентрациях субстрата В Читатель без особого труда может преобразовать уравнение (6 35а) к линейной форме типа (6 20)
Из этих вторичных графиков можно определить значение Vt и одной из констант Михаэлиса (рис. 6-5,Б и В). Два набора вторичных графиков позволяют найти все константы уравнения (6-356) (однако при этом произведение КеqAКMB рассматривается как одна константа KAB). Кинетические параметры можно определить и с помощью численных методов, которые дают возможность обрабатывать сразу все данные и получить оптимальные значения параметров. Преимущество этого подхода состоит в том, что он позволяет надежно оценить стандартные отклонения для найденных значений параметров [1].
Некоторые кинетические параметры имеют ясный физический смысл. Параметр Vf — это скорость, достигаемая при условии, когда концентрация субстрата А и концентрация субстрата В бесконечно высоки. Каждая константа Км соответствует константе Михаэлиса для простой системы, в которой концентрация второго субстрата достаточно высока, чтобы насытить фермент.
Для рассмотренной выше бимолекулярной реакции справедливы два следующих соотношения Холдейна1):
![]()
Из этих двух соотношений обычно используется только первое.
1) Входящие в эти соотношения константы задаются следующими соотношениями (см, например, Segel I Н Enzyme kinetics, J Wiley and Sons, New York, 1975, p. 564)
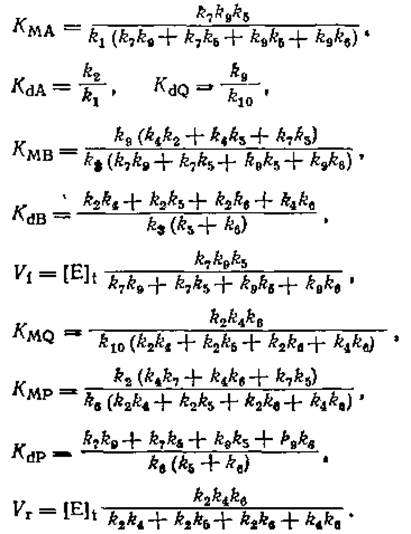
Заметим также, что константа КdA ранее обозначалась автором как KeqA — Прим. перев.
а. Механизмы типа «пинг-понг»
Особенно распространенным механизмом для ферментативных реакций, протекающих с участием кофермента, является так называемый механизм типа пинг-понг; отличительной чертой его является то, что фермент находится то в форме Е, то в форме Е':
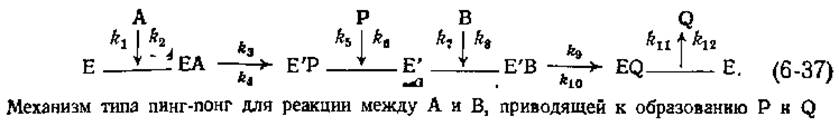
Взаимодействие фермента с субстратом А приводит к образованию формы Е' через комплекс ЕА. Е' — это модифицированная форма фермента, в которой кофермент часто оказывается химически модифицированным (примером может служить реакция переаминирования; гл. 8, разд. Д, 1). Одновременно субстрат А превращается в продукт Р, все еще связанный с ферментом. Отщепление продукта Р приводит к высвобождению формы Е', которая затем может взаимодействовать со вторым субстратом, В, и проходить вторую половину цикла с превращением формы Е' в форму Е.
Уравнения скорости для механизма типа пинг-понг напоминают по форме уравнения скорости для бимолекулярной реакции с упорядоченным присоединением субстратов (6-35а) и (6-356), однако каждое из них содержит на один член меньше1);
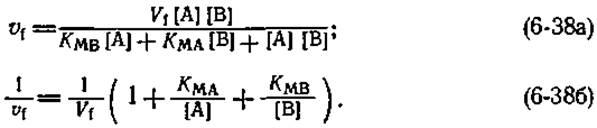
Соответственно из кинетических данных получают в этом случае на один кинетический параметр меньше, чем для реакций с упорядоченным присоединением субстратов. Кинетическая схема (6-37) для ферментативной реакции, протекающей по механизму типа пинг-понг, содержит 12 кинетических констант. Это соответствует минимальному числу стадий, которые необходимо рассмотреть, чтобы описать кинетические свойства фермента, функционирующего согласно механизму типа пинг-понг. Ясно, что из данных стационарной кинетики можно определить только часть этих констант; для оценки всех их необходимо использовать другие подходы.
Интересной особенностью механизма типа пинг-понг является то, что семейство прямых в двойных обратных координатах, которое получают при варьировании концентрации одного субстрата и фиксированных
Отметим, что если в уравнении (6-356) член КеqКMB пренебрежимо мал по сравнению с другими членами, то по своим кинетическим свойствам реакция напоминает реакции, подчиняющиеся механизму типа пинг-понг, хотя протекает согласно последовательному механизму через образование промежуточного тройного комплекса ЕАВ.
концентрациях второго, имеет другой вид, нежели семейство прямых «а рис. 6-5, Л: оно представлено прямыми, параллельными друг другу (как это выглядит на рис. 6-8 для неконкурентного ингибирования).
б. Непродуктивные комплексы
Характерной особенностью ферментативной реакции, протекающей «по механизму типа пинг-понг, является то, что в стационарном состоянии часть фермента находится в форме Е, а часть — в форме Е'. В идеальном случае форма Е обладает сродством только к А и Q, а форма "Е' — только к В и Р. Однако во многих реальных ситуациях Р и В проявляют некоторое сродство и к форме Е (а А и Q - к форме Е'). Это легко понять, поскольку продукты и субстраты часто имеют сходную структуру. Таким образом, разумно предположить, что все четыре реагента будут обладать определенным сродством как к форме Е, так и к форме Е'. Иногда способность ферментов, чья кинетика следует механизму типа пинг-понг, образовывать непродуктивные (так называемые абортивные) комплексы, имеет регуляторное значение. Изменим схему (6-37) таким образом, чтобы показать, что продукт Р обычно претерпевает ряд дальнейших превращений:
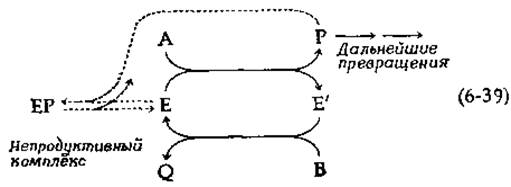
Если продукт Р накапливается в достаточно больших количествах, он может взаимодействовать с формой Е с образованием непродуктивного комплекса ЕР. Это явление представляет собой эффективную форму ингибирования продуктом, которое снимается лишь в том случае, когда в результате дальнейших превращений продукта Р его концентрация уменьшается. В литературе описаны конкретные примеры подобного типа ингибирования и рассмотрена его роль в регуляции процессов метаболизма.
в. Вывод уравнения скорости для сложных механизмов
Для простых кинетических механизмов типа рассмотренных выше вывести уравнение стационарной скорости не составляет особого труда; иное дело — более сложные механизмы. Для решения задач стационарной и нестационарной кинетики применяется топологическая теория графов. широко используемая при анализе электрических цепей [23—25]. Рассмотрим диаграмму вида
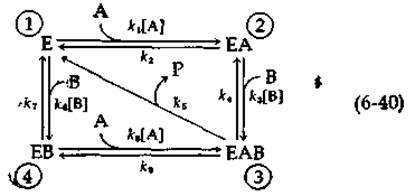
Здесь представлена реакция, в которой связывание ферментом двух субстратов (А и В) происходит неупорядоченно [схема (6-34) соответствует, напротив, случаю упорядоченного связывания субстратов]. Образующийся комплекс ЕАВ распадается на свободный фермент и единственный продукт Р. Каждая из вершин графа (6-40), пронумерованных цифрами от 1 до 4, соответствует определенной форме фермента, а каждой стрелке приписывается определенная константа скорости первого порядка или кажущаяся константа скорости первого порядка. Следуя известным правилам, можно без труда вывести уравнение стационарной скорости [1].
Преимущества использования упрощенных схематических методов становятся особенно очевидными, если рассмотреть более сложный механизм, в котором комплекс ЕАВ распадается с неупорядоченным высвобождением двух продуктов (Р и Q). Знаменатель уравнения скорости для этого механизма содержит 672 члена, и ясно, что без введения ряда упрощающих предположений получить уравнение скорости чрезвычайно трудно. В подобных сложных случаях целесообразно прибегать к помощи ЭВМ [26].
г. Допущение о быстро устанавливающемся равновесии
Уравнения скорости часто упрощаются, если одна стадия в механизме [например, стадия каталитического распада комплекса ЕАВ в схеме (6-40)] является стадией, лимитирующей скорость ферментативного процесса. В предположении, что все стадии реакции, предшествующие лимитирующей или следующие за ней, равновесны, уравнение скорости для механизма с неупорядоченным присоединением двух субстратов и неупорядоченным отщеплением двух продуктов упрощается до уравнения, аналогичного уравнению скорости в случае механизма с упорядоченным связыванием субстратов [уравнение (6-35а)]. Такое предположение действительно часто оказывается справедливым, однако в некоторых случаях (особенно для ферментов с высокой каталитической активностью) оно все же не выполняется.
д. Кинетика реакции при высоких концентрациях фермента
В опытах по изучению кинетических свойств очищенных ферментов в лабораторных условиях концентрации фермента составляют обычно 10-7—10-10 М, в то время как в клетке они равны 10-6—10-5 М и, следовательно, могут быть гораздо выше концентрации соответствующих субстратов. В связи с этим при интерпретации данных, получаемых в лабораторных условиях, необходимо соблюдать известную осторожность. В настоящее время разработаны методы анализа кинетических данных для случая, когда концентрация фермента превышает Кіл [28]; использование же обычных уравнений приводит к недопустимо большим ошибкам.