Биохимия - Химические реакции в живой клетке Том 2 - Д. Мецлер 1980
Ферменты: белковые катализаторы клеток
Основы ферментативной кинетики
Диффузия и число активных соударений фермента с субстратом
Какие факторы определяют, величину k1 в уравнении (6-14)? Эта константа скорости характеризует процесс, в ходе которого субстрат и фермент «находят» друг друга, соответствующим образом ориентируются и связываются с образованием комплекса ES. Если ориентация и связывание происходят достаточно быстро, то скорость реакции будет определяться скоростью сближения молекул за счет диффузии. Из-за частых столкновений с молекулами растворителя расстояния, на которые могут свободно перемещаться в растворе молекулы растворенного вещества, не превышают ничтожных долей их диаметра. Диффундирующие молекулы поворачиваются, вращаются, «протискиваются» между другими молекулами. Визуально этот процесс проявляется в броуновском движении микроскопических частиц, суспендированных в жидкости. Наблюдая за индивидуальной частицей, можно увидеть, что она случайно блуждает в растворе, двигаясь то в одном, то в другом направлении. Эйнштейн показал, что если измерить расстояние ∆х, на которое перемещается частица за интервал времени ∆t, то средний квадрат смещения ∆х (∆2) будет пропорционален ∆t:
∆2 = 2D∆t, (6-21)
где D — коэффициент диффузии, обычно измеряемый в см2∙с-1.
1) В случае выполнимости уравнения Михаэлиса — Ментен максимальный наклон зависимости v от lg [S] равен 2,303 Vmax/4 = 0,576 Vmаx и, следовательно, величину Vmах можно определить, разделив максимальный наклон на 0,576. — Прим. перев.
Наблюдать непосредственно за броуновским движением молекул невозможно, однако коэффициент диффузии для них может быть измерен, например, по скорости размывания границы между двумя растворами с разными концентрациями данного вещества [13]. Коэффициент диффузии для 1Н2НО (HDO) в Н2O при 25°С составляет 2,27∙10-5 см2∙с-1; тот же порядок имеют коэффициенты диффузии для ионов К+ И Сl- [14]. Для многих небольших молекул D ≃ 10-5 см2∙с-1 и уменьшается с увеличением размера молекулы. Так, для рибонуклеазы (мол. вес 13 683) D = 1,1∙10-6см2∙с-1, для миозина (мол. вес 5∙105) D ≃ 1∙10-7 cм2∙c-1. Коэффициент диффузии связан с радиусом сферической частицы r, вязкостью η и константой Больцмана k соотношением, известным под названием уравнение Стокса — Эйнштейна:
![]()
Чтобы оценить константу скорости реакции, которая контролируется частотой столкновения частиц, мы должны определить, сколько раз в секунду одна из п частиц соударяется с другой в результате броуновского движения. Впервые подход к решению этого вопроса был разработан в 1917 г. Смолуховским [15, 16], оценившим скорость, с которой частица В диффундирует ко второй частице А и вступает с ней в реакцию. Используя закон диффузии Фика, Смолуховский пришел к заключению, что число активных соударений в 1 мл за 1 с равно
Число активных соударений = 4π (DA+ DB) (rA + rB) nAnB, (6-23)
где DА и DВ — коэффициенты диффузии для частиц А и В соответственно, rA и rB — радиусы этих частиц, nA и nB — число частиц А и В в 1 мл. Число активных соударений в 1 л за 1 с равно (4π/1000) (DA+DB) (rA+rB)N2[А] [В], где N — число Авогадро. Если поделить эту величину на N, то мы придем к скорости столкновений v (выраженной в М∙с-1), которая равна скорости бимолекулярной реакции kD[А][В] (где kD — константа скорости второго порядка):
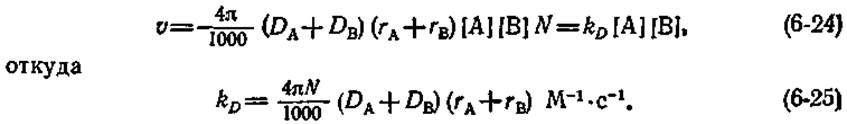
Выражение (6-25) дает слегка завышенные значения константы скорости, лимитируемой диффузией, но является все же достаточно хорошим приближением.
Если предположить, что диффундирующие частицы имеют сферичеcкую форму, то коэффициенты диффузии DA и DB можно рассчитать, при помощи уравнения (6-22); тогда уравнение (6-25) принимает следующий вид:
![]()
Обратите внимание на то, что величина kD мало меняется при варьировании отношения радиусов rА/rB. В большинстве случаев можно допустить, что rA ≈ rB, и тогда уравнение (6-26) сводится к
![]()
Bязкость воды при 25°С равна — 0,01 П (1 П=10-5 Н∙см-2), и из уравнения (6-27) мы получаем, что kD≈0,7∙1010 М-1∙с-1. Как показал Дебай [17], проведенные расчеты верны лишь для незаряженных сферических частиц; в случае же заряженных частиц константу скорости kD нужно умножить на поправочный множитель. Этот поправочный множитель для субстрата и фермента, несущих два-три заряда, равен 5—10 и приводит к увеличению или уменьшению скорости реакции (в зависимости от знака заряда).
Другой, довольно простой вывод уравнения (6-27) предложил Д. Френч1). Рассмотрим небольшой элемент объема ∆V, захватываемый частицей при ее перемещении в растворе на расстояние, равное ее собственному радиусу. Этот элемент объема равен
∆V = πr2 x r = πr3 (6-28)
и захватывается за интервал времени, который можно оценить из уравнения (6-21): ∆t = r2/2D. Подставляя сюда выражение для D (6-22), получаем следующее соотношение:
![]()
Из уравнений (6-28) и (6-29) находим объем, захватываемый одной частицей за 1 с:
![]()
Поскольку радиус столкновения двух частиц одинакового размера равен удвоенному радиусу частицы, эффективный объем, захватываемый двумя частицами, будет в четыре раза превышать объем, определяемый уравнением (6-30). Так как диффундируют обе частицы, эффективный коэффициент диффузии вдвое больше того коэффициента диффузии, который фигурирует в уравнении (6-25). В результате эффективный объем, захватываемый частицей за 1 с, будет в восемь раз превышать объем, рассчитанный по формуле (6-30). Объем, захватываемый одним молем частиц, равен kD (напомним, что константа скорости второго порядка имеет размерность л∙моль-1∙с-1). Таким образом, если выражение (6-30) умножить на 8 и перейти к молярной концентрации, то оно будет идентично уравнению Смолуховского (6-27).
Уравнение (6.30) дает значение объема ∼1,4∙10-11 см3, который соответствует объему куба с ребром ~2,4 мкм. Если мы сопоставим эту величину с объемом клетки (см. табл. 1-2) или органеллы, то увидим, что объем, захватываемый молекулой фермента за 1 с, составляет довольно заметную часть объема небольшой по размеру клетки, митохондрии, хлоропласта и т. д.