Биохимия - Химические реакции в живой клетке Том 2 - Д. Мецлер 1980

Ферменты: белковые катализаторы клеток
Основы ферментативной кинетики
«Эффект клетки» и вращение молекул

Интересно сопоставить константу скорости второго порядка для активных соударений, рассчитанную по теории Смолуховского [т. е. при помощи уравнения (6-26)], с константой скорости второго порядка А для молекулярных столкновений, получаемой из кинетической теории тазов:

1) Личное сообщение Д. Френча, которому автор очень благодарен за обсуждение «опросов теории соударений. Результаты этого обсуждения частично опубликованы ранее (18].

В этом выражении m_A и m_B — массы частиц А и В соответственно, k_B — константа Больцмана. Константа скорости k также довольно слабо зависит от размера молекул и для сферических частиц варьирует от 4∙10¹¹ до 11∙10¹¹ М^-1∙с^-1, т. е. немного больше чем на порядок превышает константу скорости для активных соударений. Молекулы газа сталкиваются и тут же отскакивают друг от друга. В растворе же они после первого столкновения продолжают сталкиваться с почти неизменной частотой, и в результате на каждое активное соударение приходится 100—200 столкновений двух частиц. Во время одиночного активного соударения частицы находятся вместе в «клетке» растворителя; это обстоятельство является очень важным для протекания ферментативных реакций.

За время активного соударения субстрата и фермента обе молекулы случайным образом поворачиваются, поэтому последовательные столкновения застают их в различных взаимных ориентациях. В одной из таких ориентаций комплементарные поверхности (т. е. субстрат и субстрат-связывающий центр) оказываются в непосредственной близости друг к другу, что приводит к образованию «продуктивного» комплекса ES.

Вращение молекул в растворе описывается количественно законом, диффузии (аналогичным закону Фика), где вводится коэффициент вращательной диффузии 0 [19, 20]. Рассмотрим группу молекул, ориентация которых в начальный момент времени одинакова, а затем случайным образом меняется в результате вращательной диффузии. Ориентацию каждой молекулы будем характеризовать углом а:

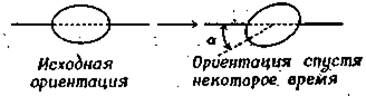
В начальный момент cos а = 1, a по мере изменения ориентации случайным образом среднее значение cos а, полученное усреднением по всем молекулам, стремится к нулю. Временем вращательной релаксации т называют время, необходимое для уменьшения среднего значения cos a в е раз (при этом a становится равным 68,5°). Для молекул сферической формы справедливо следующее соотношение:

Молекулы, имеющие форму эллипсоида вращения или палочки, характеризуются двумя значениями коэффициента вращательной диффузий, а молекулы, размеры которых различны по всем трем осям, — тремя.

Допустим, что диаметр небольшой сферической молекулы субстрата составляет 1 нм, а диаметр сферической молекулы фермента — 5 нм. Значения θ для этих молекул при η = 0,01 П, рассчитанное при помощи уравнения (6-32), равны соответственно

Как мы видим, молекулы меньшего размера вращаются гораздо быстрее, чем крупные молекулы, и времена вращательной релаксации небольших по размерам белков имеют тот же порядок, что и константа kВ для активных соударений, частота которых лимитируется диффузией. Однако для очень больших молекул (особенно для длинных, имеющих форму палочки) время вращательной релаксации вокруг короткой оси может составлять уже доли секунды.