Принципы структурной организации белков - Г. Шульц 1982

Структурная роль пептидной связи
Конформационная энергия

Модель жестких сфер — хорошее приближение. Данные Рамачандрана и сотр. [28, 29], выражаемые —ψ-картой (которую часто называют «карта Рамачандрана», см. рис. 2.3, б), подтверждаются результатами, полученными при исследовании кристаллических глобулярных белков. На рис. 2.4 сведены все — и ψ-углы, найденные в 13 белках. Самая высокая плотность распределения экспериментальных точек наблюдается вблизи (—60°, —60°) в положении правой а-спирали, что отражает высокое содержание а-спиралей в глобулярных белках. Другой максимум в распределении находится вблизи (—90°, +120°) и отвечает вытянутой цепи с остатками, образующими ß-складчатый лист. Поскольку плотность вблизи (—90°, 0°) также довольно высока, отталкивание между N_i и не настолько существенно, как это следует из модели жестких сфер.

Область, отвечающая левой а_L-спирали, заполнена довольно слабо по сравнению с соседними областями. Левую а_L-спираль пока еще не удалось наблюдать. Около 10% точек попадают в области, запрещенные для всех остатков кроме Gly, на правую и нижнюю левую части диаграммы. Исходя из частоты Gly, указанной в табл. 1.1, и допуская равномерное распределение остатков Gly по доступному для них конформационному пространству, можно было бы ожидать появления только половины из этих точек. Следовательно, около 5% всех остатков, содержащих С_β-атомы, находятся в запрещенной области. Этот факт подтверждают более точные картины распределения для восьми белков, на которых —, ψ-величины нанесены отдельно для каждого типа остатков [31]. Следует помнить, однако, что использованные экспериментальные данные также могут содержать ошибки, вызванные неправильной интерпретацией карт электронной плотности.

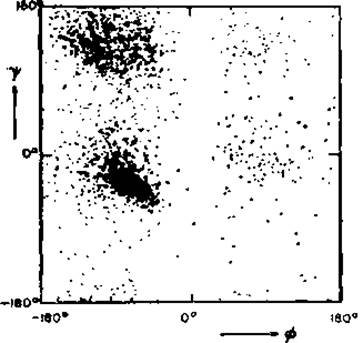
Рис. 2.4. Двугранные углы основной цепи для приблизительно 2500 остатков 13 белков [30]. Эту карту иногда называют картой Рамачандрана.

Карта потенциальной энергии более точно выявляет стерические препятствия. Модель жестких сфер представляет довольно грубый подход к описанию стерических затруднений. Ясно, что его можно улучшить, используя вместо жестких сфер набор функций потенциальной энергии. Карты потенциальной энергии были рассчитаны многими авторами [32—34] для всевозможных остатков. В качестве примера на рис. 2.5 приведена карта потенциальной энергии для аланина. Какого-либо качественного различия по сравнению с картой жестких сфер здесь нет. Потенциальные энергии правой a_R-спирали и левой а_L-спирали выше, чем энергия вытянутой цепи, примерно на 0,5 и 2,5 ккал/моль соответственно. В случае правой а_R-спирали это увеличение энергии кажется преодолимым благодаря выгодности прочного водородного связывания внутри а-спирали. У левой а_L-спирали нет явных структурных преимуществ по сравнению с правой. Обе спирали представляют собой цилиндры одинаковой формы. Поэтому если в структуре нужен цилиндр, нет причин для использования энергетически невыгодной левой a_L-спирали, если другая спираль может с успехом выполнить то же назначение.

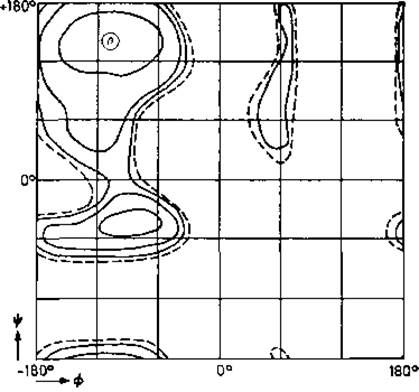
Рис. 2.5. Распределение потенциальной энергии в плоскости (—, ψ) для пары пептидных звеньев с остатком Ala между ними [34].

Карта построена с параметрами пептидной связи Полинга—Кори (рис. 2.1,а). Изоэнергетические линии проведены с интервалом 1 ккал/моль в отрицательную область от нуля. Нулевая эквипотенциаль показана штрихами. Отмечено положение скрученного ß-листа. Потенциальная поверхность изменится, если учесть водородные связи с пептидными звеньями, удаленными по цепи (например, в а-спирали).

На карте потенциальной энергии виден низкоэнергетический перешеек между областью вытянутой цепи (—, ψ) = (—120°, +120°) и областью а-спирали (—60°, —60°). Такого мостика нет в модели жестких сфер, даже если использовать предельно малые контактные радиусы. Поскольку эта так называемая мостиковая область, согласно данным по кристаллическим белкам (рис. 2.4), отличается высокой заселенностью, она и в действительности легко доступна. Модель жестких сфер в этом случае приводит к ошибкам. Стерические затруднения между атомами N_i и H_i+1 (рис. 2.3, а), возникающие при этих углах, компенсируются благодаря диполь-дипольному взаимодействию, соответствующему слабой водородной связи. Подобные взаимодействия были найдены в кристаллах модельных соединений [35].

Пептидная связь обладает некоторой гибкостью. Конформационные карты на рис. 2.3 и 2.5 построены в предположении жесткой пептидной связи, имеющей параметры Полинга — Кори (рис. 2.1,а). Дальнейшее уточнение модели требует введения потенциалов изменения валентных углов, длин связей и торсионного вращения вокруг пептидной связи. Это, естественно, делает конформационное пространство одного остатка многомерным, а любое непосредственное использование или исчерпывающее описание — затруднительным. Приведем для оценки отклонения, отвечающие увеличению потенциальной энергии на 1 ккал/моль:

Кроме того, следует также учитывать выходы атомов из плоскости [36]. В принципе, гибкость можно учесть на двумерной энергетической карте, если допустить возможность всех гибких деформаций и в каждом случае рассчитать минимальную энергию для данной пары углов —, ψ. Отметим, что если принимать во внимание гибкость всех звеньев остова, его конформацию нельзя описать только значениями углов — и ψ.

Таким образом, если пептидная связь обладает заметной гибкостью, то конформационная карта, построенная при фиксированных параметрах этой связи (рис. 2.5), может оказаться неточной в тех областях, которые отвечают слабым стерическим затруднениям, как, например, в областях, разрешенных только для Gly, поскольку их можно устранить небольшими отклонениями валентных и торсионных углов, а также длин связей. Этим объясняются те 5% случаев на рис. 2.4, в которых значения —, ψ попадают в области, запрещенные, согласно модели жестких сфер, из-за стерического взаимодействия с С_β-атомом.