Принципы структурной организации белков - Г. Шульц 1982

Статистическая механика перехода спираль - клубок
Модель Зимма - Брэгга для перехода спираль - клубок
Связь между s и температурой

Вблизи точки перехода относительный статистический вес линейно связан с температурой. Эта связь важна, так как переходы спираль — клубок часто наблюдаются при изменении температуры. Ее можно получить, если вновь обратиться к уравнению (А.4), но свести его к двум состояниям

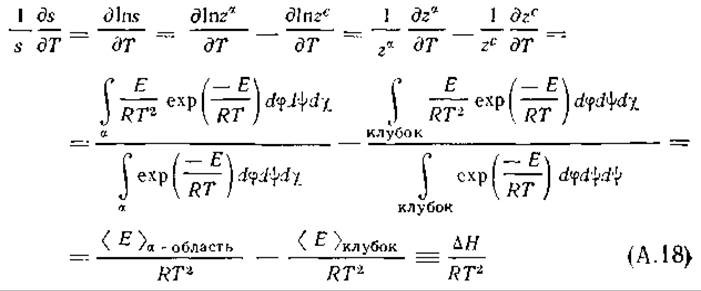
Таким образом, в области перехода (s ≃ 1) относительное изменение s в зависимости от Т приблизительно постоянно, т. е. изменение s приблизительно пропорционально изменению температуры (рис. А.2).

Температура перехода

Температура перехода приблизительно пропорциональна изменению энтальпии. Переход происходит при s = 1, то есть при z^a = = z^c или

Если принять, что Е = Еa = const по всей a-области размера Ω_а и Е = Е_с = const по всей области клубка размера Ω_c, то

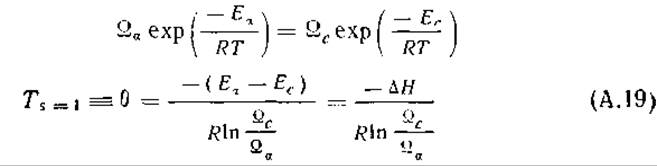
Переходы происходят лишь в тех случаях, когда состояние с более низкой энергией занимает меньшую конформационную область. При Ω_с > Ω_а температура перехода становится отрицательной, если энергия а-конформации менее выгодна, чем энергия конформации клубка, Е_а > Е_с. Кроме того, переходы совершаются

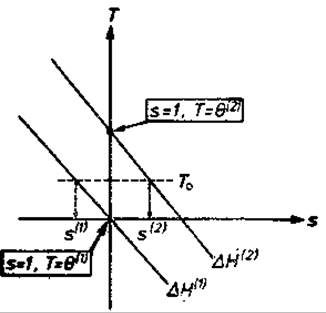
Рис. А.2.

Связь между относительным статистическим весом s, температурой Т и разницей энтальпий ∆Н вблизи точки перехода (s = 1, T = θ) для двух различных полимеров.

Это — графическое представление уравнений (А.18) и (А.19). Обе величины ∆Н (¹) и ∆Н(²) отрицательны и ∆Н(²)<∆Н(¹). Различие температур перехода θ(²)—θ(¹) пропорционально разности ∆H(²) — ∆Н(¹). При данной температуре То оба полимера имеют различные относительные статистические веса s(¹) и s(²). Эти значення s определяют склонности полимеров к образованию спирали при данной температуре.

в том случае, когда состояние с меньшей энергией Е (более прочное связывание) занимает меньшую конформационную область 2. В нашем примере, когда 2_а (рис. 2.3), спиральная конформация принимается, только если она энергетически выгодна. Направление перехода таково, что при температурах ниже θ превалирует состояние с меньшей энергией, а при температурах выше θ — состояние с большей конформационной областью (рис. А.2). Чем выше температура перехода θ, тем меньше различие конформационных областей и тем больше энергетически выгодных спиральных конформаций.