Структура и функционирование белков. Применение методов биоинформатики - Джон Ригден 2014

Динамика белков: от структуры к функционированию
Молекулярно-динамические расчеты
Принципы и приближения

Несмотря на значительный прогресс в алгоритмах, основная теория, на которую опираются МД расчеты, довольно проста. Для биомолекулярных систем, имеющих N частиц, численное решение временного уравнения Шредингера

для N-частичной волновой функции ψ(r,t) системы невозможно. Поэтому необходимы некоторые приближения, позволяющие моделирование соль-ватированной биомолекулы на временных масштабах порядка наносекунд.

Первое из них относится к расположению ядер и электронов: благодаря гораздо меньшей массе и, следовательно, гораздо большей скорости электронов по сравнению с ядрами, электроны часто можно считать мгновенно приспосабливающимися к движению ядер. Таким образом, в приближении Борна-Оппенгеймера нужно рассматривать только движение ядер, влияние на которое электронных степеней свободы описывается поверхностью потенциальной энергии V(r). Второе существенное приближение, используемое в МД, состоит в классическом описании движения ядер с помощью законов Ньютона

где m_i и r_і - это масса и положение і-того ядра. Для получения потенциальной энергии V(r) нужно решить уравнение Шредингера для электронных степеней свободы при классическом описании движения ядер. Однако ввиду большого числа участвующих электронов необходимо дальнейшее упрощение, состоящее во введении полуэмпирических силовых полей, которые аппроксимируют V(r) большим числом функционально простых энергетических термов для валентных и невалентных взаимодействий. В общем виде

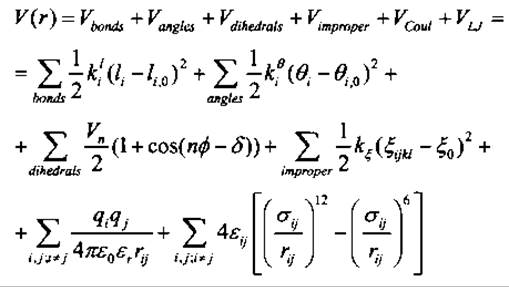
Эти простые термы часто имеют гармонический вид (например, V_bonds, V_angles, V_improper) или обусловлены физическими законами (например, законом Кулона V_Соul и законом Леннарда-Джонса V_LJ). Термы описываются своей функциональной формой и небольшим числом параметров, таких как атомный радиус в случае ван-дер-ваальсовых взаимодействий. Все параметры определяются либо из ab initio квантово-химических расчетов, либо из сравнения структурных или термодинамических данных с подходящими средними величинами для молекулярно-динамических ансамблей малых молекул. Число энергетических термов, их функциональная форма и индивидуальные параметры могут сильно варьироваться между различными силовыми полями (Brooks et al. 1983; Weiner et al. 1986; Van Gunsteren and Berendsen 1987; Jorgensen et al. 1996).

Исходя из вышеприведенного описания белка как системы точечных масс (с координатами r_j и скоростями v_i), движущихся в классическом потенциальном поле под действием внешних сил F_i, стандартный МД расчет с дискретным шагом по времени At, лежащем в фемтосекундном диапазоне, интегрирует ньютоновские уравнения движения по некоторой численной схеме, например, используя алгоритм с перескоками (leap-frog algorithm (Hockney et al. 1973)):

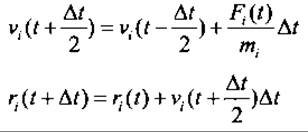
Несмотря на взаимодействие с мембранами и другими макромолекулами, основной окружающей средой белков является вода. Для расчета модельной системы, которая приближена к in vivo системе насколько это возможно, белок должен быть сольватирован путем добавления молекул воды и ионов в физиологической концентрации. В расчетной ячейке, заполненной белком и растворителем, могут возникнуть такие артефакты, связанные с границей раздела сред, как испарение, высокое давление из-за поверхностного натяжения и ориентация молекул растворителя на поверхности. Чтобы избежать этих артефактов, часто используют периодические граничные условия. В этом случае в модельной системе исчезают поверхности вообще, что, в свою очередь, может привести к новым артефактам, если молекула оказывается искусственно взаимодействующей со своим изображением из-за, например, дальнодействующих электростатических взаимодействий. Эти присущие периодичности артефакты могут быть сведены к минимуму увеличением размера расчетной ячейки. Различные формы ячеек, например, куб, додекаэдр или усеченный октаэдр позволяют наилучшим образом подобрать ячейку для конкретной формы белка и, таким образом, достичь компромисса между числом молекул растворителя и расстоянием между молекулой белка и её изображением.

Поскольку среда растворителя сильно влияет на структуру и динамику белков, то параметры воды должны быть аккуратно подобраны. Несмотря на появление моделей неявного растворителя, где вода представляется непрерывной средой вместо индивидуальных “явных” молекул (Still et al. 1990; Gosh et al. 1998; Jean-Charles et al. 1991; Luo et al. 2002), в наше время используются и разнообразные явные модели (e.g. Jorgensen et al. 1983). Эти модели различаются числом частиц, используемых для представлення молекулы воды и размещения статических парциальных зарядов, отражающих полярность и, по сути, в большинстве силовых полей, поляризацию. Поскольку эти заряды в процессе расчета остаются постоянными, эффекты явной поляризации исключаются. В настоящее время есть несколько моделей воды (и силовых полей) с поляризуемостью (см. недавний обзор Warshel et al. (2007)).

При решении ньютоновских уравнений движения общая энергия системы сохраняется, приводя к микроканоническому ансамблю NVE с постоянным числом частиц N, объемом V и энергией Е. Однако реальные биологические системы с доступными для моделирования размерами постоянно обмениваются энергией со своим окружением. Кроме того, имеется постоянное давление Р, обычно равное атмосферному (1 бар). Чтобы учесть эти особенности, были созданы алгоритмы, позволяющие поддерживать постоянные температуру и давление (Anderson 1980; Nose 1984; Berendsen et al. 1984), что приводит к каноническому ансамблю NPT.