Биологические мембраны - А. Н. Огурцов 2012

Электрогенез биомембран
Неравновесная термодинамика биомембран
Линейная неравновесная термодинамика

Если в системе действуют n сил, вызывающих n потоков, то для установления функциональной зависимости между ними нужно экспериментально определить n x n феноменологических коэффициентов.

В действительности число независимых феноменологических коэффициентов меньше - их число может быть меньше по следующим причинам.

Во-первых, оказывает влияние симметрия системы - в случае симметричной изотропной среды каждый поток необязательно должен сопрягаться со всеми силами,

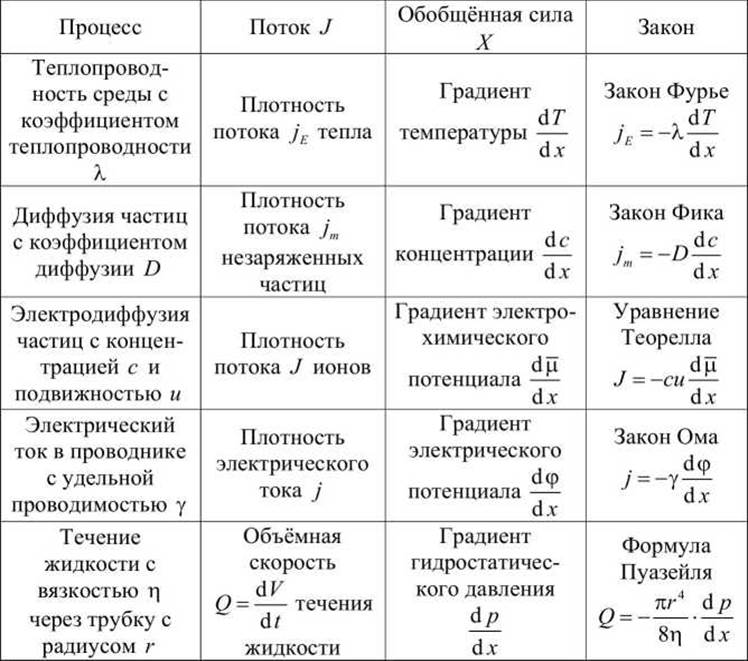
Таблица 6 - Примеры линейных необратимых процессов

Во-вторых, справедлива теорема Онзагера или соотношение взаимности Онзагера - феноменологические коэффициенты образуют симметричную матрицу, т. е.

В-третьих, несопряжённые (і = j) коэффициенты всегда положительны

Lu > 0.

Действительно, рассмотрим систему, в которой есть только два потока, например, температуры q и вещества d, тогда

Поскольку

то

Пусть, далее, исчезает температурный градиент, а остаётся только концентрационный, т. е. X_q = 0, X_d≠ 0, тогда следовательно, L_dd > 0. Аналогично, оставляя только температурный градиент, можно показать, что L_qq > 0. Кроме того, (L_qd + L_dq)² < 4L_qqL_dd, откуда следует

В общем случае для линейных систем и для произвольного числа сил и потоков можно показать, что и

Сформулируем (без доказательства) ещё несколько основных положений линейной неравновесной термодинамики неравновесных процессов.

Как уже говорилось выше, второе начало термодинамики требует выполнения условия которое относится к сумме в целом.

Oтдельные члены этой суммы могут быть отрицательными. Это означает, что отдельный, индивидуальный, поток J_i с J_iХ_i < 0 невозможен, поскольку это противоречит второму началу термодинамики. Однако, благодаря сопряжению с другими потоками J_j, для которых J_jX_j > 0, в открытой системе оказывается возможным поток, немыслимый в системе изолированной. Должно лишь выполняться условие

Сопряжение потоков определяется отличием от нуля недиагональных сопряжённых коэффициентов L_ij.

Например, смесь двух газов в сосуде, стенки у которого находятся при различных температурах, самопроизвольно разделяется так, что у горячей стенки больше содержание одного газа, у холодной - другого. Это явление называется термодиффузией. Поток вещества идёт в направлении, противоположном направлению падения концентрации, так как он сопряжён с потоком теплоты, идущим от горячей стенки к холодной. Дефицит энтропии в одном процессе перекрывается её избыточным производством в другом.

Мы видим, что производство энтропии в открытой системе в принципе обеспечивает протекание процессов, невозможных в изолированных системах. Это принципиально важно для понимания эндергонических процессов в биосистемах.

Сопряжение химических реакций в открытой системе делает возможным протекание эндергонических реакций (реакций при которых возрастает свободная энергия системы), которые запрещены в изолированных системах.

Например, образование каждой пептидной связи при синтезе белка происходит с выделением одной молекулы воды. Так как в клетке вода содержится в избытке, то должна преобладать обратная реакция - реакция гидролиза пептидных связей. Синтез полипептидной цепи становится возможным благодаря сопряжению реакции синтеза с экзергонической реакцией расщепления (гидролиза) АТФ и функция диссипации в целом положительна.

Сопряжение эндергонических процессов с гидролизом АТФ имеет общее значение в биологии. Посредством сопряжения реализуется универсальная роль АТФ как донора свободной энергии, необходимой для протекания эндергонических процессов. Если бы клетки и организмы были изолированными системами, АТФ не могла бы играть этой роли.

Неравновесная термодинамика уже в линейном приближении доказывает возможность протекания в открытых системах процессов, запрещённых в изолированных системах. Это имеет фундаментальное значение для биологии.

Принцип Кюри-Пригожина. Потоки и силы могут быть как скалярными, так и векторными. В изотропной системе (в системе, свойства которой одинаковы во всех направлениях) на сопряжение потоков накладывается ограничение, известное как принцип Кюри-Пригожина, смысл которого заключается в том, что невозможно сопряжение между скалярными потоками (например, химические реакции) и векторными потоками (например, потоки вещества, тепловые потоки) - скаляр не может быть причиной вектора и вектор - скаляра (сила не может быть причиной потока, имеющего другую тензорную размерность).

Другая формулировка этого принципа: внешние воздействия, вызывающие различные явления, не могут обладать более высокой симметрией, чем порождаемый ими эффект.

Принцип Кюри-Пригожина справедлив и для случая анизотропной системы, имеющей в состоянии равновесия центр симметрии. Во всех остальных случаях анизотропии, а также в нелинейной области (когда отклонения системы от состояния равновесия нельзя считать малыми и нельзя пренебрегать нелинейными членами ряда Тейлора), когда свойство изотропии исчезает независимо от структуры среды при равновесии, принцип Кюри-Пригожина неприменим.

Теорема Пригожина. Открытая система может находиться в стационарном, хотя и неравновесном состоянии. В этом состоянии продукция энтропии внутри системы в точности компенсируется оттоком энтропии в окружающую среду, так что суммарная энтропия системы не меняется

Такое стационарное состояние называется состоянием проточного равновесия.

Наглядная модель такого состояния представлена на рисунке 165.

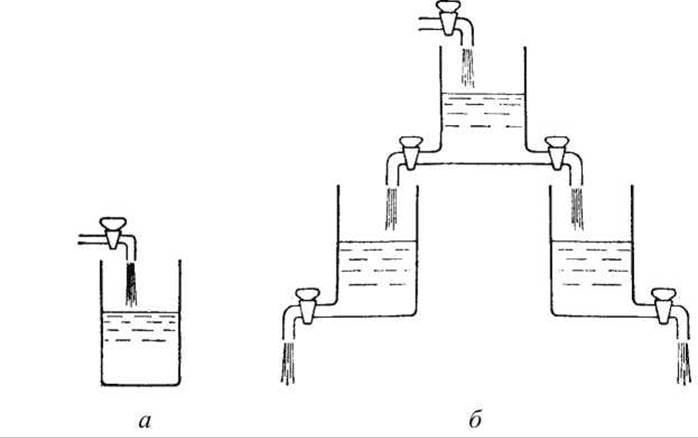
Рисунок 165 - Модель, иллюстрирующая состояние проточного равновесия открытой системы: а - закрытая система, 6 - модель открытой системы

Уровень жидкости в промежуточном сосуде установится в некотором положении, определяемом тем, насколько открыты краны, соединяющие сосуды. Изменяя повороты кранов можно установить новые уровни жидкости - новое стационарное состояние проточного равновесия.

Стационарное состояние открытой системы реализуется, если на систему наложены ограничения, фиксирующие постоянные значения части обобщённых сил, а остальные обобщённые силы могут меняться.

Например, пусть в системе действуют две обобщённые силы Х₁ и Х₂, первая из которых фиксирована X₁ = const (например, первая сила - это фиксированный градиент температур, который не меняется).

Как было показано выше, производство энтропии описывается соотношением

Поскольку L₂₂ > 0, то вторая производная по X₂ (при X₁ = const)

Следовательно, в стационарном состоянии выполняется теорема Пригожина: В стационарном состоянии, близком к равновесию, продукция энтропии σ минимальна.