Универсальные поурочные разработки по Физике 8 класс к учебнику А. В. Перышкина
Период и частота обращения. Решение задач - Кинематика
Цели: ввести и изучить новые характеристики вращательного движения
Ход урока
I. Повторение. Проверка домашнего задания
Урок можно начать с краткого опроса по теме предыдущего урока:
- Как меняется величина и направление скорости тела в равномерном движении по окружности?
- Что характеризует центростремительное ускорение?
- От каких величин зависит центростремительное ускорение?
- Какие точки поверхности Земли движутся с большим центростремительным ускорением: точки экватора или точки на широте 45°?
- Как меняется центростремительное ускорение, если при постоянной скорости уменьшается радиус окружности?
Во время опроса двое учеников выписывают на доске решения домашних задач. Затем решения коллективно обсуждаются, исправляются ошибки.
II. Изучение нового материала
План изложения нового материала:
1. Период вращения при движении по окружности.
2. Частота обращения при движении по окружности.
1. Переходя к изложению нового материала, нужно отметить, что он - логическое продолжение изученного на прошлом уроке.
Любое периодическое движение, а равномерное движение тепа по окружности таким и является, характеризуется периодом и частотой вращения.
Время, в течение которого совершается один полный оборот, называется периодом обращения.
В физике период обозначается буквой Т. Если за время t тело совершает 4 оборота, то время одного оборота будет равно: T = t/4.
Пусть t = 10 с, тогда Т = t/4 = 2,5 с.
Таким образом:
![]()
где t - время, n - число полных оборотов за время t.
В системе СИ период измеряется в секундах.
Т = [с].
2. Очень часто движение по окружности характеризуют частотой обращения. Она обозначается буквой v (v - ню).
Под частотой обращения v понимают число оборотов за единицу времени. Пусть тело за время t = 2 с совершило n = 10 оборотов. Тогда частота обращения будет равна:
![]()
Очень легко найти связь между периодом и частотой:
![]()
или:
![]()
Формально, частота v - величина, обратная периоду Т.
При равномерном движении тела по окружности период или частоту можно найти и из иных соображений. Если тело движется по окружности радиуса R со скоростью v, то период обращения можно найти из условия:
![]()
где s - длина окружности, s = 2πR. Тогда:
![]()
III. Решение задач
Последнюю часть урока желательно посвятить решению задач.
Задача 1
Тело движется со скоростью 2 м/с по окружности радиуса 1 м. Определить период и частоту обращения. Чему равно центростремительное ускорение?
Дано:
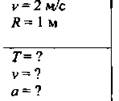
Решение:
Так как ![]() то
то ![]()
![]()
(Ответ: Т = 3,14 с, v = 0,32 с-1, а = 4 м/с2.)
Задача 2
Точильный круг за t = 1 мин совершает 1800 оборотов. Найти период и частоту обращения.
Дано:
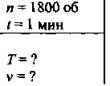
Решение:
Так как ![]() то
то ![]()
![]()
(Ответ: Т = 1/30 с, v = 30 с-1.)
Домашнее задание
1. § 6 учебника; вопросы и задания к параграфу.
2. Задачи и упражнения (учебник, с. 126) № 32-35.
3. Сборник задач В. И. Лукашика, Е. В. Ивановой, № 170.