Универсальные поурочные разработки по Физике 8 класс к учебнику А. В. Перышкина
Равномерное движение теля по окружности - Кинематика
Цели: изучить один из простейших видов криволинейного движения - движение тела по окружности.
Демонстрации: движение шарика по закругленному желобу.
Ход урока
I. Повторение. Проверка домашнего задания
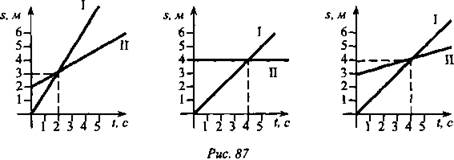
При проверке домашнего задания особое внимание следует уделить глубокому пониманию графического представления движения. Нескольким ученикам можно раздать карточки с индивидуальными заданиями, например: по графикам I и II путей двух равномерно движущихся тел (рис. 87) определить скорость каждого тела. У какого тела скорость больше? Ответ обосновать.
Необходимо также вспомнить формулы скорости и пути при равноускоренном движении.
II. Изучение нового материала
План изложения нового материала:
1. Скорость при равномерном движении по окружности.
2. Демонстрация движения шарика по закругленному желобу.
3. Ускорение при равномерном движении по окружности.
1. Прежде чем приступить к изложению нового материала учитель задает классу ряд вопросов, подготавливающих к восприятию новой темы:
- По какой линии полетит камень, вращающийся на нити, если нить внезапно обрезать? (Ответы учащихся.)
- Автомобиль движется по криволинейной траектории с постоянной по модулю скоростью. Можно ли утверждать, что его ускорение в этом случае равно нулю?
Переходя к изложению нового материала, следует заметить, что помимо равнопеременного движения по прямой, часто встречается равномерное движение тела по окружности. При этом числовое значение скорости остается неизменным, а вот направление скорости тела постоянно изменяется.
Очень наглядный опыт с точильным кругом (а такие есть в лабораториях физики) подтверждает факт изменения направления скорости искр при затачивании деталей. При движении по окружности в любой точке скорость тела направлена по касательной к этой окружности (см. рис. 88).
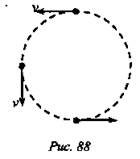
2. В демонстрации с движением шарика по закругленному желобу можно убедиться, что шарик при сходе с желоба продолжает движение по касательной.
3. С другой стороны, любое изменение скорости указывает на наличие ускорения. При равномерном движении по окружности это ускорение отвечает за быстроту изменения направления скорости.
- Как определить направление этого ускорения в равномерном движении по окружности?
Ясно, что оно не может совпадать по направлению со скоростью или быть направленным встречно, ибо это привело бы к изменению величины скорости.
При данном типе движения ускорение в любой точке направлено к центру окружности (см. рис. 89).
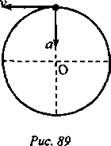
Данное ускорение называют центростремительным ускорением. В любой точке траектории угол между скоростью и ускорением равен 90°.
Центростремительное ускорение определяется по формуле:
![]()
Эту формулу на уроке выводить не стоит, так как вывод достаточно сложный.
- Итак, от каких величин зависит центростремительное ускорение? (От скорости движения и радиуса окружности.)
- Два тела движутся с одинаковыми скоростями по окружностям. У какого тела центростремительное ускорение больше: у того, что движется по окружности с большим радиусом, или у того, которое движется по окружности с меньшим радиусом?
III. Решение задач
Если на уроке остается время, желательно у доски разобрать одну-две задачи по изученному материалу.
Задача 1
Определить центростремительное ускорение тела, которое движется по окружности радиуса 20 см со скоростью 10 м/с.
Дано:
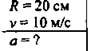
Решение:
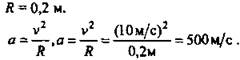
(Ответ: а = 500 м/с.)
Домашнее задание
1. § 5 учебника; вопросы и задания к параграфу.
2. Задачи и упражнения (учебник, с. 126) № 27-30.
3. Сборник задач В. И. Лукашика, Е. В. Ивановой, № 169.