Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Кинетика процессов утилизации субстрата, образования продуктов метаболизма и биомассы в культурах клеток
Структурированные модели кинетики клеточного роста
Моделирование клеточного роста как оптимального процесса
Изучение роста микроорганизмов на смесях различных субстратов показывает, что обычно организмы быстрее усваивают субстрат, обеспечивающий наиболее высокую скорость роста.
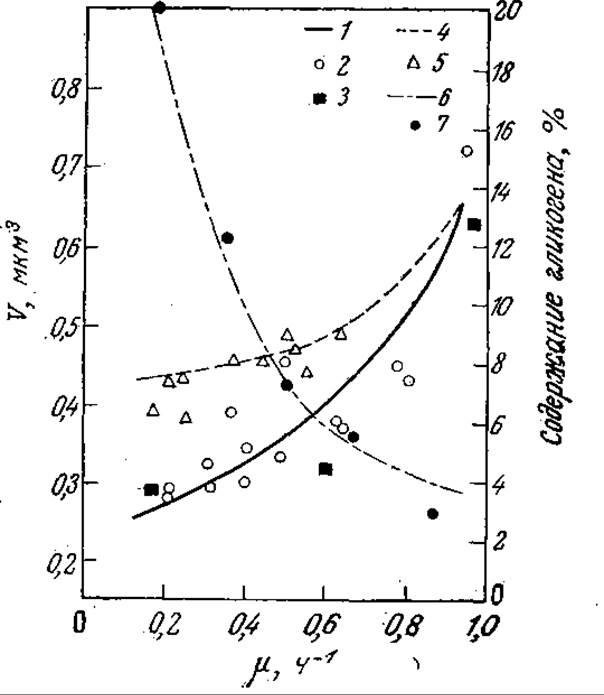
РИС. 7.27. Сравнение результатов, предсказываемых моделью изолированной клетки, с экспериментальными данными. Приведены расчетная кривая (1) изменения объема клетки при лимитируемом глюкозой росте (2, 3 — экспериментальные данные); то же (4) при лимитируемом ионом аммония росте (5 — экспериментальные данные); расчетная кривая (6) изменения процентного содержания гликогена (7 — экспериментальные данные). [Воспроизведено с разрешения из работы: Shuler М. L., Domach М. М., Mathematical Models of the Growth of Individual Cells, in Foundations of Biochemical Engineering, Blanch H. W., Papoutsakis E. T., Stephanopoulos G., (eds.), p. 101, American Chemical Society, Washington, 1983.]
На молекулярном уровне в основе такого поведения микроорганизмов лежат процессы индукции, репрессии, ингибирования и активации, рассмотренные в гл. 3 и 6. Их можно положить в основу соответствующих моделей кинетики роста (разд. 7.5.3), но для этого нужно учитывать множество параметров и детальных сведений о механизме процессов. В альтернативном подходе, разработанном Рамкришной и сотрудниками, влияние регуляторных клеточных процессов описывается как результат оптимизации клеточного роста [21, 22]. В основе этого подхода лежит постулат о том, что в результате естественного отбора и эволюции биологические системы приобрели способность использовать среду оптимальным образом. С точки зрения такой кибернетической модели действие регуляторных систем метаболизма можно описать как решение задачи оптимального распределения ресурсов, обеспечивающего максимальную скорость роста.
Основанный на законе соответствия для распределения ресурсов алгоритм оптимизации оказался вполне пригодным для моделирования клеточного роста на смешанных субстратах. Если отдача от утилизации ресурса Zi равна Θi(Zi) и если полная отдача (сумма всех Θi) максимизирована при условии», что сумма всех Zi равна постоянной величине, то должен удовлетвоpяться следующий закон соответствия:
![]()
Предположим, что скорость роста популяции зависит от внутриклеточных концентраций е1, e2, ... ряда ферментов, необходимых для ассимиляции субстратов S1, S2, ... — соответственно. В таком случае, например, вклад субстрата Si в образование биомассы может быть описан уравнением
![]()
где
![]()
Весовой коэффициент vi определяется условиями закона соответствия для энергетического выхода процессов потребления различных субстратов, которые предполагают, что
![]()
где vj — энергия, высвобождающаяся при утилизации единицы массы субстрата j. Применение закона соответствия к распределению клеточных ресурсов для синтеза ферментов приводит к следующему выражению для скорости синтеза фермента Еi;
![]()
где
![]()
Важным преимуществом этой модели является возможность экспериментального определения всех кинетических параметров в реакциях с индивидуальными субстратами. Метод оптимизации учитывает все аспекты кинетики роста популяции микроорганизмов в среде с несколькими субстратами. На рис. 7.28 приведено сравнение расчетных и экспериментальных данных по росту культуры бактерии Klebsiella oxyloca в среде, содержащей арабинозу и лактозу. Соответствующие параметры модели, определенные в отдельных экспериментах, можно найти в работе [22]. В данном случае модель хорошо отражает продолжительную лаг-фазу между периодом роста на лактозе и периодом более медленного роста на арабинозе. Изучение других моделей этого класса показало, что расчетные и экспериментальные данные не только качественно, но и количественно хорошо согласуются и в случае трехфазного роста микроорганизмов на трех субстратах, как в периодическом процессе, так и в стационарной и переходной фазах непрерывного процесса в ПРПП. Большой интерес представило бы распространение кибернетического подхода на другие методы оптимизации и процессы образования продуктов жизнедеятельности клеток. Кибернетические модели являются интересной альтернативой моделей, в которых метаболизм рассматривается как упрощенная сеть химических реакций.
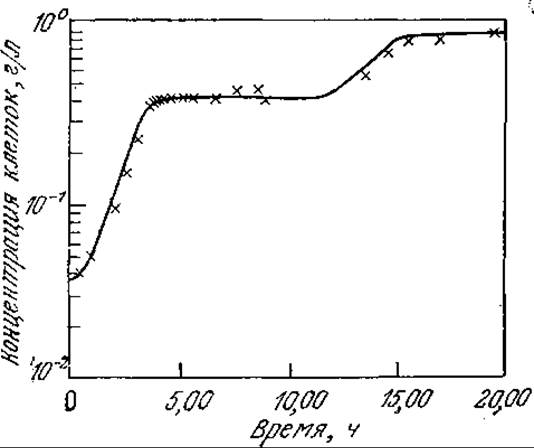
РИС. 7.28. Сравнение экспериментальных (х) и полученных с помощью кибернетической модели расчетных (-------) данных для двухфазного периодического роста Klebsiella oxyloca в арабинозно-лактозной среде. [Воспроизведено с разрешения из статьи: Kompala D. S., Ramkrishna D., Tsao G. T., Cybernetic Modeling of Microbial Growth on Multiple Substrates, Biotech. Bioeng., 26, 1272 (1984).]