Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Кинетика процессов утилизации субстрата, образования продуктов метаболизма и биомассы в культурах клеток
Кинетика образования продуктов метаболизма
Моделирование кинетики образования продуктов метаболизма на основе механизмов молекулярных превращений; генетически структурированные модели
Чем точнее описание кинетики в модели отражает действительно осуществляющиеся в клетке химические события, тем более универсальной становится наша модель. Здесь под «универсальностью» мы понимаем возможность получения удовлетворительных результатов в условиях, отличающихся от используемых в ходе разработки модели и определения ее параметров. Механизмы белкового синтеза, имеющего большое значение в производстве ферментов, гормонов и других практически важных полипептидов, изучены настолько глубоко, что становится возможной разработка моделей на уровне молекулярных событий и взаимодействий. Подобные модели должны быть в высшей степени универсальными и полезными в оптимизации параметров среды и генетической природы организма.
Материальный баланс по мРНК, образующейся при транскрипции данного гена G, можно выразить следующим уравнением (здесь квадратные скобки служат для обозначения молярных концентраций данного компонента в клетке, выраженных в молях в единице объема клетки) [27]:
![]()
В этом уравнении kp — константа общей скорости транскрипции, a kd — константа скорости инактивации и(или) деструкции мРНК; допускается, что оба последних процесса имеют первый порядок. В уравнении (7.98) учтен также коэффициент эффективности утилизации промотора η, отражающий модуляцию транскрипции оператором. Во многих случаях, представляющих практический интерес, оценка η в единицах концентраций белка-эффектора и индуктора или репрессора является наиболее важным этапом всего моделирования.
Аналогично можно записать и уравнение материального баланса по внутриклеточному продукту трансляции, т. е. по исследуемому белку:
![]()
Здесь скорость синтеза белка пропорциональна концентрации кодирующей данный белок мРНК и эффективности ее утилизации на рибосомах (можно достаточно обоснованно предположить, например, что изменение нуклеотидной последовательности в связывающем рибосому центре приведет к изменению величины I). В этом случае мы опять принимаем, что реакция инактивации белка имеет первый порядок.
При сбалансированном росте производные от [мРНК] и [Р] по времени равны нулю, и при этом условии из уравнений (7.98) и (7.99) следует, что
![]()
Это уравнение непосредственно выражает концентрацию внутриклеточного белка через параметры, характеризующие экспрессию гена и мРНК, а также стабильность белка в клетке.
Таблица 7.6. Значения3 параметров модели кинетики экспрессии генов в Е. colia
Параметр |
Значение |
Размерность |
kр |
2400/(233μ-2 + 78) |
мин-1 |
kq |
3600а/ (82,5μ-1 + 145) а = 1 при μ > ln2 а = μ/ln2 при μ < 1n 2 |
мин-1 |
kd |
0,46 |
мин-1 |
ke |
0,07 |
мин-1 |
a В таблице приведены средние значения, которые могут потребовать уточнений при расчете скорости экспрессии определенного гена и синтеза соответствующего белка. Для удельной скорости роста μ здесь принята размерность ч-1.
«Данные из статьи: Lee S. В., Bailey J. Е., Analysis оf Growth Rate Effects on Productivity of Recombinant Escherichia coli Populations, Biotech. Bioeng., 26, 66 (1984).
В табл. 7.6 приведены характерные средние значения параметров описанной модели для синтеза белка в Е. coli, отражающие найденные зависимости параметров скоростей транскрипции и трансляции от скорости роста.
Имеющиеся в настоящее время данные свидетельствуют о том, что во многих случаях скорость экспрессии генов в Е. coli лимитируется стадией транскрипции. Следовательно, скорость экспрессии регулируемого оператором гена зависит от эффективности транскрипции этого гена, которая в свою очередь определяется совместным влиянием модулирующих агентов на сайты оператора и связывания РНК-полимеразы. В качестве примера рассмотрим систему промотор-оператор гена lac Е. coli, причем основное внимание будем уделять совместному влиянию /ас-репрессора, индуктора и ДНК на экспрессию гена и, следовательно, на ß-галактозидазную активность [28].
Количество продуцируемого фермента пропорционально эффективности утилизации промотора т), которая в свою очередь пропорциональна вероятности того, что операторный сайт О не связан с белком-репрессором R. Таким образом,
![]()
Здесь [О] о — общая концентрация операторных сайтов в клетке Е. coli. Дробное выражение в правой части уравнения (7.101) можно определить, если учесть взаимодействия между R, О, другими неспецифическими сайтами ДНК (D), индуктором I; предполагается, что все эти взаимодействия равновесны:
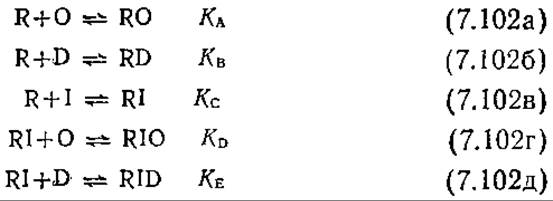
Оператор О может существовать в трех различных формах, концентрации которых можно связать следующим уравнением материального баланса:
![]()
Аналогично уравнение материального баланса по R можно записать в виде
![]()
Поскольку концентрация [D] неспецифично связывающих сайтов ДНК выше общей концентрации R, мы можем принять, что
![]()
Используя приближение (7.105), равновесную природу реакций (7.102), уравнение материального баланса (7.104) и пренебрегая членами с множителем [O]0/[R]0, нетрудно прийти к следующему уравнению:
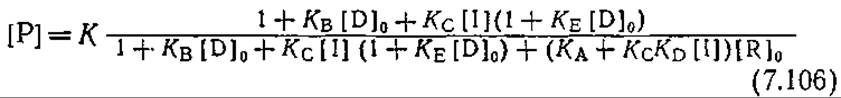
Опубликованные в литературе экспериментальные данные позволяют приближенно, с точностью не ниже одного порядка величин, оценить параметры этого уравнения [28J:
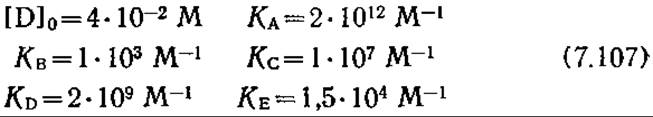
Оценка параметров этой математической модели требует обширных экспериментальных данных, но вместе с тем моделирование с учетом молекулярных взаимодействий имеет и свои преимущества. Так, ее параметры имеют строгое физико-химическое толкование и часто могут быть определены в отдельных экспериментах in vitro. Более того, модель такого уровня обладает особой характеристикой, называемой генетической структурой. Под генетической структурой в данном случае понимается четкая зависимость определенных параметров модели от генетической природы; так, изменение нуклеотидной последовательности lас-оператора должно сопровождаться изменением параметров Ка и КD, характеризующих взаимодействия lас-оператора с белком-репрессором. По мере развития и углубления наших знаний о механизмах взаимодействий в системе ДНК —белок, вероятно, мы сможем учитывать влияние определенных изменений нуклеотидной последовательности на соответствующие константы связывания ДНК с белком расчетным путем. Тогда разработанная на молекулярном уровне кинетическая модель позволит осуществлять картирование нуклеотидной последовательности, отражающее продуктивность популяции клеток. Потенциальные возможности такого подхода для рациональной количественной оптимизации генетической модификации организма (или, по меньшей мере, клонированных участков ДНК) очевидны.
В качестве примера рассмотрим применение уравнения (7.106) для расчета влияния концентрации репрессора на скорости индуцированной и неиндуцированной транскрипции lac- промотора-оператора хромосомы Е. coli. Необходимые экспериментальные данные, в том числе внутриклеточные концентрации репрессора для каждого из мутантов, известны для мутантных штаммов i-, iqи isqЕ. coli. Эти величины можно непосредственно использовать при моделировании; они не влияют на другие параметры модели. Как показано в табл. 7.7, модель удовлетворительно отражает влияние внутриклеточной: концентрации репрессора как в присутствии индуктора, так и без индуктора. В приведенной в конце главы литературе можно^ найти другие примеры моделирования с учетом регуляции на молекулярном уровне.