Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Кинетика процессов утилизации субстрата, образования продуктов метаболизма и биомассы в культурах клеток
Сегрегированные модели кинетики клеточного роста и образования продуктов метаболизма

Обычно популяции клеток гетерогенны в том смысле, что составляющие популяцию индивидуальные клетки различаются по размерам, возрасту, скорости роста и другим свойствам. Чтобы модель кинетики роста популяции клеток в большей степени приближалась к реальной ситуации, она должна отражать и распределение клеток по различным категориям, обладающим разными биохимическими активностями. Другим преимуществом такого подхода к моделированию является возможность установления связи между особенностями клеточного цикла и другими свойствами изолированной клетки, с одной стороны, и общими характеристиками популяции — с другой. Основной недостаток сегрегированных моделей обусловлен их математической сложностью. В этой связи в настоящем разделе основное внимание мы будем уделять распределению по возрастам и коррелированным распределениям популяций клеток, размножающихся бинарным делением. Вывод уравнений материального баланса популяций, использующихся в сегрегированных моделях, и решение уравнений модели для случая некоторых микробных систем приведены в работах [29—31].

Частотная функция возраста клеток W (а) позволяет определить относительное количество клеток в возрасте от а до a + da как W (а) da. В этом разделе символом а мы будем обозначать возраст клетки, считая, что нулевой возраст соответствует только что возникшим в результате деления клеткам, а делящиеся клетки имеют возраст t_D, равный продолжительности клеточного цикла или времени удвоения индивидуальной клетки. Для сбалансированного экспоненциального роста популяции основанное на возрасте клеток уравнение баланса популяции будет выглядеть следующим образом:

Здесь μ — общая удельная скорость роста популяции. Поскольку все клетки популяции имеют возраст от 0 до t_D, то W

должно также удовлетворять условию

В результате деления не всегда образуются две жизнеспособные клетки. Причиной может быть старение клеток или их гибель, а также рост содержащей неустойчивые плазмиды популяции в селективной среде. Если символом Θ обозначить долю жизнеспособных дочерних клеток, образующихся в результате бинарного деления жизнеспособной клетки, то уравнение баланса, связывающее количества делящихся и новых жизнеспособных клеток, можно записать в следующей форме:

Решение уравнения (7.108) с учетом условий (7.109) и (7.110) дает

Из уравнений (7.110) и (7.111) следует приведенное ниже выражение для зависимости между скоростью роста μ, и временем генерации клетки:

Поскольку среднее время удвоения популяции (средняя продолжительность клеточного цикла) равна

то

Таким образом, если 0 не равно нулю, то t_D меньше Это относительно простое соотношение иллюстрирует очень важный общий принцип: общие кинетические свойства популяции не обязательно должны соответствовать кинетическим параметрам на уровне индивидуальной клетки.

Во многих случаях для расчета различных частотных функций и усредненных свойств популяции, имеющих конкретное физическое содержание, можно использовать функцию плотности возраста, которую нельзя непосредственно определить. Предположим, например, что синтез некоторых компонентов клетки или продуктов ее жизнедеятельности осуществляется с постоянной скоростью в определенный период клеточного цикла от а₁ до а₂. Установлено, в частности, что в эукариотах ДНК синтезируется только в периоде S. Сообщалось также, что некоторые ферменты синтезируются рядом организмов только в течение очень узкого временного интервала клеточного цикла. В таких случаях скорость образования продукта жизнедеятельности клеток можно выразить уравнением

Для рассмотренной выше ситуации получим

Для любого количественного параметра клеточного роста х (например, клеточной массы, содержания белка, объема, возможно также содержания определенного продукта метаболизма), непосредственно связанного с возрастом клеточного цикла а (иными словами, если а можно выразить или определить как функцию от х), частотную функцию для а можно преобразовать в частотную функцию для х в соответствии с уравнением

Предположим, например, что в течение клеточного цикла масса отдельной клетки возрастает во времени по линейному закону:

m(a) = m₀ + ak (7.118)

так, что

Если в уравнение (7.117) подставить значения W из (7.111 и а из (7.119), то получим

Здесь опять-таки следует подчеркнуть различие между кинетикой роста отдельной клетки и популяции клеток. Масса отдельной клетки может возрастать в соответствии с уравнением (7.118) (такая зависимость для некоторых организмов была обнаружена и экспериментально), в то время как общая масса популяции этих же клеток возрастает экспоненциально, например в соответствии с уравнением (7.37), описывающим кинетику сбалансированного роста популяции в периодическом процессе. Одно из преимуществ сегрегированного подхода к моделированию кинетики клеточного роста заключается в возможности выяснения непосредственной взаимосвязи между параметрами кинетики и регуляции роста индивидуальной клетки и параметрами кинетики роста популяции клеток.

Если допустить, что плотность клеточного вещества постоянна, то уравнение (7.120) можно также интерпретировать как функцию распределения клеток по объему, которое можно определить экспериментально с помощью счетчика Коултера или методами проточной цитометрии по рассеянию света (см. гл. 10). На практике, однако, чаще измеряют количественные характеристики популяции в целом. Эти характеристики можно вычислить с помощью соответствующих частотных функций и уравнения

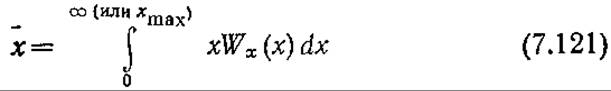
В других подходах к моделированию гетерогенность популяции клеток можно рассматривать с иных точек зрения. Предложено несколько математических моделей образования продуктов жизнедеятельности в популяциях микроорганизмов, учитывающих длительные эффекты старения. В модели Пинг Шу удельная скорость образования продукта жизнедеятельности клеток выражается как

где θ — общее] время пребывания клеток в реакторе [32]. Тогда концентрацию продукта жизнедеятельности в момент времени t периодического процесса можно вычислить по уравнению

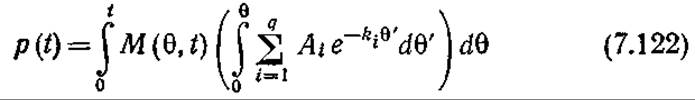
Здесь М(θ,t)—частотная функция в момент времени t концентрации клеточной массы, время пребывания которой в реакторе равно 0. Поскольку клеточное вещество, имеющее в момент t возраст 0, образуется за время t—θ, отсюда следует, что

M(θ,t) = r_x(t - θ) (7.123)

Эта модель отличается известной универсальностью и пригодна для описания различных механизмов накопления продуктов метаболизма, наблюдаемых в периодических микробиологических процессах.