Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Процессы переноса в биотехнологических системах
Массообмен с участием свободно поднимающихся и свободно падающих тел
Коэффициенты массопередачи для газовых пузырьков и потоков пузырьков
Коэффициент массопередачи для пузырька газа представляет собой коэффициент пропорциональности между общей плотностью потока пузырьков и общей движущей силой массопередачи (сl* — сl). Локальная плотность потока на границе раздела фаз газ — жидкость равна —DO2(dc/dz)z=0(справедливо при низких скоростях массопередачи), где z — координата, измеренная в жидкой фазе. Таким образом,
![]()
или в безразмерных параметрах:
![]()
Относительная (безразмерная) концентрация с вблизи границы раздела фаз может быть найдена путем решения уравнений переноса:
![]()
Используя это выражение для оценки производной ![]() в уравнении (8.28), в принципе можно выразить искомый коэффициент массопередачи klчерез число Шервуда:
в уравнении (8.28), в принципе можно выразить искомый коэффициент массопередачи klчерез число Шервуда:
![]()
Таким образом, безразмерный коэффициент массопередачи Sh является функцией только двух параметров — Sc и Gr. Здесь D — характерный диаметр пузырьков.
В литературе описаны к другие выражения для коэффициентов массопередачи для случая опускающихся или поднимающихся пузырьков, капелек или твердых частиц, в которых применялись иные критерии подобия, например число Рейнольдса (Re = рlDu/μl) или число Пекле (Pe = uD/DO2). В этих безразмерных параметрах u — скорость пузырьков газа относительно скорости жидкости. И в первом и во втором случае выражение скорости и через разность плотностей ∆р = (рl - pg) приводит в соответствии с уравнением (8.30) к зависимости коэффициента массопередачи только от Gr и Sc.
Массопередачу из изолированной сферы с жесткой границей раздела фаз (эта модель достаточно точно описывает систему, состоящую из небольших пузырьков в культуральной жидкости в присутствии поверхностно-активных веществ) можно определить теоретически для случая Re ≡ plDu/μl ≪ 1 и Pe ≡ uD/DO2 ≫ 1. (Таким образом, uD/DO2 ≫ 1 ≫ plDu/μl, откуда следует, что μl/рlDO2 = Sс ≫ 1. Может ли быть справедливым обратное неравенство?) В водных средах, кинематическая вязкость которых (v = μl/рl) составляет приблизительно 10-2см2/с, а DO2 равен примерно 10-5 см2/с, число Шмидта обычно имеет величину порядка 103. Следовательно, при Re = 10-1—10-2 применимо полученное расчетным путем уравнение
![]()
Для малых чисел Рейнольдса, при которых применимо уравнение (8.31), конечная скорость ut сферы определяется уравнением
![]()
Подстановка ut из уравнения (8.32) в уравнение (8.31) дает
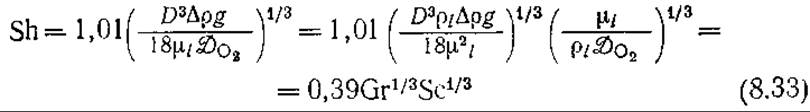
[Выражение (D3∆pg)μlDO2 известно также как число Рэлея Ra.] Обратите внимание на то, что здесь, как и следовало ожидать, Sh = f(Gr, Sc).
В случае больших чисел Рейнольдса для одиночного нециркулирующего сферического пузырька в ламинарном режиме предложено другое уравнение:
![]()
Интересно, что здесь Sh изменяется пропорционально квадратному (а не кубическому) корню из параметра относительной скорости; это свидетельствует об изменении гидродинамического режима. Опять-таки, подстановка вместо и выражения для соответствующей конечной скорости приведет к Sh = f(Gr, Sc).
Во многих промышленных реакторах с барботажем воздуха (рис. 8.2) воздушные пузырьки группируются в потоки, в которых они соприкасаются настолько тесно, что течение в дисперсной системе и массопередачу вблизи границы раздела фаз газ — жидкость уже нельзя достаточно точно описать моделью, учитывающей гидродинамические характеристики и массопередачу для изолированного пузырька. Согласно данным Калдербэнка и Му-Янга, адсорбцию ограниченно растворимых газов в жидкостях, реагирующих с этими газами, можно описать с помощью всего лишь двух уравнений [10]. Существуют два принципиально различных режима массопередачи с участием потоков пузырьков; граница между этими режимами определяется критическим диаметром пузырьков Dc. В отсутствие поверхностно-активных веществ Dc ≈ 2,5 мм. Более крупные пузырьки обычно возникают в перемешиваемых реакторах с чистой водой и в колоннах с ситчатыми тарелками. Пузырьки меньшего диаметра характерны для колонн с тарелками из спеченного материала, а также для перемешиваемых сосудов, содержащих водные растворы гидрофильных веществ.
При D < Dc = 2,5 мм
![]()
При D > Dc = 2,5 мм
![]()
Из уравнений (8.33) и (8.35) следует, что в потоке пузырьков при одних и тех же значениях Sc и Gr коэффициент массо- передачи приблизительно на 20% ниже по сравнению с изолированными пузырьками с неподвижной поверхностью. Показано, что уравнение (8.36) справедливо и для эрлифтных систем (рис. 8.2, а), если вместо коэффициента 0,42 ввести коэффициент 0,50.
Изменение показателя степени числа Шмидта в уравнении (8.36) [по сравнению с уравнением (8.35)] свидетельствует об изменении гидродинамического режима. В случае ньютоновских жидкостей, вязкость которых постоянна и не зависит от скорости сдвига (обусловленной скоростью перемешивания, скоростью движения пузырьков и другими факторами), переход от области D < Dc к области D > DCсопровождается изменением формы пузырьков от почти сферической (небольшие пузырьки) до полусферической и грибообразной. Более подробно вопрос о гидродинамике потоков пузырьков рассмотрен в работе [10]. На величину Dcвлияют поверхностно-активные вещества; сообщалось, что в некоторых средах Dc достигает величины 7,0 мм. В некоторых неньютоновских жидкостях, которые мы рассмотрим позднее, переход от одного режима массопередачи к другому совершается более плавно; в таких системах нет резкого скачка, характерного для ньютоновских жидкостей.
Результаты изучения массопередачи в случае малых частиц показывают, что по мере снижения разности плотностей ∆р число Шервуда приближается к низшему пределу 2,0. В случае суспензий отдельных клеток, их скоплений, хлопьевидных образований и т. д., а также в случае эмульсий газойля или других углеводородов более точно значение числа Шервуда определяется уравнением
![]()
или
![]()
Отсюда следует, что относительный вклад чисто диффузионного эффекта (∆р = 0, kl = 2,0DO2/D) уменьшается по мере увеличения размеров частиц. Для изолированной клетки 2DO2/D равно приблизительно 0,1 см/с, в то время как второе слагаемое, являющееся производным от числа Рэлея, равно 0,01 см/с; следовательно, массопередача вблизи поверхности клетки близка к массопередаче сферы в относительно неперемешиваемой среде. Большие размеры хлопьев, пленок и т. п. обусловливают значительное повышение относительного вклада второго слагаемого.