Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Процессы переноса в биотехнологических системах
Массообмен с участием свободно поднимающихся и свободно падающих тел
Определение площади поверхности раздела фаз и газосодержания дисперсной системы
Определив по той или иной из приведенных выше формул kl, мы далее должны найти площадь поверхности раздела фаз а', приходящуюся на единицу объема. Значение а' можно оценить расчетным путем по известному диаметру отверстий барботирующего устройства и по другим данным о конструкции реактора, а также путем фотографирования процесса или иными методами. Если время пребывания пузырька в реакторе равно tb, объемная скорость потока в расчете на одно отверстие барботера F0, а общее число (одинаковых) отверстий n, то площадь поверхности границы раздела фаз в единице объема а' (если пренебречь коалесценцией и изменением D в результате изменения гидростатического давления или абсорбции) определяется уравнением
![]()
Ниже мы рассмотрим параметры правой части уравнения (8.39), в частности, детально изучим физические факторы, определяющие размер пузырьков, и на этой основе оценим возможность определения размера пузырьков расчетным путем как функции от параметров работы реактора, конструкции смесителя и свойств жидкой среды. Многие из приведенных здесь, концепций, относящихся к системам с поднимающимися отдельными пузырьками или потоком пузырьков, применимы и для изучения процессов переноса в реакторах с механическим перемешиванием.
Размер пузырьков в биологических реакторах определяют три важнейших взаимосвязанных фактора; аналогичные факторы играют основную роль и в формировании дисперсии второй ограниченно растворимой жидкой фазы. К этим факторам oтносятся механизм образования пузырьков, их распад на меньшие пузырьки и коалесценция (слияние пузырьков). Образование пузырьков обусловлено неустойчивостью поступающего в жидкую фазу газового потока, что приводит к разрыву единой струи на отдельные пузырьки. Распад пузырьков зависит от конкуренции между поверхностным натяжением, стабилизирующим пузырек, и локальными гидромеханическими силами, стремящимися его разрушить.
Вероятность коалесценции пузырьков определяется свойствами поверхности раздела фаз газ — жидкость. В обычных для процессов биохимической технологии водных системах на коалесценцию влияют в первую очередь растворенные в жидкой фазе вещества, например жирные кислоты, полиспирты, электролиты, кетоны. Добавление этих веществ подавляет коалесценцию. В последующем обсуждении мы рассмотрим два крайних случая: коалесцирующие дисперсные системы (например, воздух — чистая вода) и некоалесцирующие дисперсные системы (например, воздух — водный раствор электролита).
Наш анализ мы начнем с изучения процесса образования пузырьков газа при его поступлении с объемной скоростью F0 через единственное отверстие диаметром d. Символом D0 мы будем обозначать начальный диаметр образующегося пузырька. В этой ситуации можно различать два режима. При низких скоростях потока газа в отверстии формируется последовательно один пузырек за другим. Простейший подход к анализу такого режима основан на изучении равновесия сил, приложенных к покидающему отверстие пузырьку. Это происходит в тот момент, когда выталкивающая сила (пD03∆pg)/6 уравновешивается удерживающей силой пσd:
![]()
Подробнее теория этого вопроса изложена в работе [21].
При некоторой критической скорости потока газа F0* в отверстии барботера наблюдается переход от отдельных пузырьков газа к непрерывной струе. Методы точного расчета F0* в настоящее время не разработаны; известно, однако, что критическая скорость потока газа должна находиться в диапазоне
![]()
Если скорость газового потока выше F0*, то газовые пузырьки образуются путем разрыва газовой струи вследствие неустойчивости поверхности раздела фаз. Разработанная Рэлеем теория устойчивости предсказывает, что диаметр пузырьков, образующихся в результате разрыва газовой струи при ламинарном течении жидкой фазы, приближенно должен быть равен
D0 = dl(12п/0,485)1/3 = 4,27d (8.42)
при условии, что [21]
![]()
В процессах биохимической технологии это условие обычно выполняется.
При введении газового потока в вязкую культуральную среду основное сопротивление образованию новых пузырьков оказывает не столько поверхностное натяжение пузырьков, сколько вязкость жидкой среды. Если пузырьки образуются, то отношение диаметров пузырька и отверстия барботера (D/d) определяется уравнением
![]()
Здесь относящиеся к отверстию барботера числа Рейнольдса и Фруда задаются уравнениями (8.45) и (8.46) соответственно:

Иногда в дисперсной системе газ — жидкость пузырьки газа имеют меньший диаметр, чем на выходе из распределяющего газ устройства. Причиной этого явления может быть неустойчивость пузырьков под действием сил, прилагаемых к ним движущейся непрерывной фазой. Для диспергированной жидкой или газовой фазы в непрерывной жидкой фазе максимальный размер (диаметр) свободно поднимающихся (опускающихся) или перемещаемых за счет перемешивания пузырьков или капель диспергированной фазы определяется равновесием противодействующих сил:
1. Динамического давления т (суммы разностей напряжения сдвига и нормального напряжения), стремящегося придать каплям вытянутую форму и в конце концов разделить их на меньшие капли; этому процессу препятствуют две указанные ниже силы.
2. Сил поверхностного натяжения σ/D частицы, стремящихся вновь придать капле сферическую форму, отвечающую минимальной поверхностной энергии.
3. Сопротивлением диспергированной фазы деформации, обусловленным ее вязкостью; это сопротивление пропорционально ![]() (здесь индекс d отражает принадлежность
(здесь индекс d отражает принадлежность
параметра к диспергированной фазе).
В системах газ — жидкость сила 3 пренебрежимо мала по сравнению с силой 2. В дисперсных системах типа жидкость — жидкость сила 3 должна быть относительно большой, но, как мы увидим позднее в примере 9.2, даже в этом случае силы поверхностного натяжения играют главную роль.
Эффект двух последних факторов уменьшается пропорционально D-ß, где ß — положительное число. Отсюда следует, что при некоторой критической величине диаметра Dcдинамическое давление преодолеет два противодействующих сопротивления и пузырьки или капли распадутся на меньшие частицы. Критическому диаметру, очевидно, должно соответствовать следующее равенство:
![]()
где m1 и m2 — константы.
Если силы поверхностного натяжения намного превосходят силы, обусловленные вязкостью диспергированной фазы, то при критическом диаметре пузырьков
![]()
Согласно уравнениям (8.48) максимальный размер пузырька равен частному от деления произведения безразмерной константы m1 и поверхностного натяжения на динамическое давление. Следовательно, повышение динамического давления приведет к распаду пузырьков все меньшего диаметра.
В теоретических или эмпирических уравнениях, описывающих взаимосвязь между максимальным диаметром устойчивого пузырька (или капли) и свойствами жидкой среды и течения, обычно применяется критерий подобия, основанный на уравнениях (8.48). Так, число Вебера We определяется как
![]()
Критическое число Вебера Wecесть не что иное, как значение We при D = Dc; согласно уравнению (8.48), Wecявляется характерной константой. Экспериментальным путем и теоретическими расчетами показано, что для системы чистый воздух — вода Weс приблизительно равно единице (точнее, Wec = 1,05).
Чтобы с помощью изложенных концепций и уравнений вычислить максимальный диаметр устойчивых пузырьков, нам необходимо определить значения динамического давления т, соответствующие различным режимам течения. Для свободно поднимающихся пузырьков т определяется по уравнению
![]()
Здесь ut — конечная скорость пузырьков, которую в случае сферических пузырьков можно определить по уравнению (8.32). В сложном турбулентном течении определение динамического давления затруднено. Турбулентность следует ожидать, например, в барботажных колоннах вблизи аэрирующего сопла. Впервые столкнувшись здесь с этой проблемой, мы перейдем к обсуждению некоторых связанных с турбулентностью понятий общего характера, которые полезны и при рассмотрении ряда последующих тем.
В разработанной А. Н. Колмогоровым и другими исследователями статистической теории турбулентности поле турбулентного течения рассматривается как результат суперпозиции вихрей или флуктуаций скоростей, характеризующихся масштабом длины или частотой флуктуаций и величиной. Наиболее крупномасштабные вихревые элементы или первичные вихри имеют масштаб основного течения. Эти первичные вихри нестабильны и распадаются на меньшие, которые в силу своей неустойчивости распадаются на еще более мелкомасштабные вихри и так далее. Этот каскад превращений крупномасштабных вихрей в мелкомасштабные сопровождается потоком кинетической энергии, пока в конце концов она не рассеется в виде теплоты. Поток кинетической энергии через каскад вихрей приводит к тому, что направленный характер первичных вихрей (зависящий от геометрии реактора, конструкции сопел, мешалок и т. п.) постепенно затухает. Теория Колмогорова утверждает, что мелкомасштабные вихри статистически не зависят от первичных вихрей и локально изотропны (пространственно однородны). Масштаб длины λ0 наиболее мелкомасштабных вихрей, которые рассеивают энергию турбулентности, определяется уравнением
![]()
где P/Vl— потребляемая мощность, приходящаяся на единицу объема.
При изучении влияния турбулентности обычно используют усредненные во времени параметры. Так, среднеквадратичная скорость urms ≡ <u2(t)>1/2(скобки О обозначают усреднение во времени мгновенных флуктуаций скорости) отражает среднюю величину изменений локальных скоростей. Для масштабов длины l, намного меньших масштабов первичных вихрей и намного больших λ0, зависимость среднеквадратичной скорости вихрей от характерного масштаба I определяется выражением
![]()
где а — константа.
Возвращаясь к проблеме нахождения выражения для динамического давления, которое могло бы быть затем использовано для определения числа Вебера, отметим, что мы можем воспользоваться уравнением
![]()
Это выражение является мерой турбулентного напряжения сдвига, действующего на пузырек диаметром Dc. Из уравнений (8.49), (8.52) и (8.53) получаем
![]()
Здесь а' — константа. Таким образом, повышение потребляемой мощности на единицу объема приводит к уменьшению максимального размера устойчивых пузырьков.
Существенно, что, согласно теории изотропной турбулентности, приходящаяся на единицу объема потребляемая мощность является важнейшим параметром, определяющим как масштаб образующихся вихрей, так и интенсивность турбулентных флуктуаций скорости, сравнимых по масштабу длины с размерами пузырьков и капель. Локальная изотропная турбулентность представляет собой теоретическое явление, далеко не всегда наблюдаемое на практике; тем не менее нам важно не забывать физическую интерпретацию механизма передачи энергии (энергии сжатого газа или механического перемешивания) газовым пузырькам, каплям, хлопьям или гранулам мицелия. Кроме того, уравнения (8.52) и (8.54) предполагают, что величина P/Vl будет оказывать существенное влияние на коэффициенты массопередачи в барботажных колоннах и резервуарах с перемешиванием. Особо следует подчеркнуть еще один важный аспект этой теории: основную роль играет количество энергии, приходящееся на единицу объема, а не способ ее передачи. Не играет большой роли, например, передается ли энергия потоком сжатого газа или перемешивающим устройством, не существенна и конструкция последнего и т. д. Это обобщение опять-таки носит теоретический характер, однако в ряде случаев теоретические и соответствующие экспериментальные данные хорошо согласуются.
Рассмотрев независимо процессы коалесценции, образования и распада пузырьков, мы можем теперь перейти к изучению различных возможных типов взаимодействия этих процессов в барботажной колонне. Сначала предположим, что в рассматриваемой двухфазной дисперсной системе медленно происходит коалесценция пузырьков. Если начальный диаметр пузырьков D0 меньше максимального диаметра устойчивых пузырьков Dc, характерного для условий наибольшего динамического давления (в барботажной колонне обычно в области формирования пузырьков), то характерный размер пузырьков будет равен D0 (табл. 8.3). Если же D0 больше Dc, то следует ожидать распада пузырьков на более мелкие с характерным диаметром Dc.
Таблица 8.3. Зависимость характерного диаметра пузырьков D от их тенденции к коалесценции и соотношения между диаметром пузырьков в момент образования (D0) и максимальным диаметром устойчивых пузырьков (Dc)
Начальные условия |
Некоалесцирующая система |
Коалесцирующая система |
D0 < Dc |
D ≈ D0 |
Переход к равновесной: дисперсной системе |
D0 > Dc |
D ≈ Dc (барботаж, перемешивание) |
D ≈ Dc (локальное равновесие) |
С другой стороны, если коалесценция происходит быстро, то образующиеся пузырьки будут сливаться и увеличиваться в. размерах до тех пор, пока их диаметр не превысит Dc. Тогда начнется обратный процесс распада пузырьков. В этом случае начальный размер пузырьков D0 может сохраняться только в области барботера и практически не влияет на действительный размер пузырьков в реакторе. Учитывая, что флуктуации скоростей в турбулентном режиме, а следовательно, и Dc в общем случае различны в разных точках реактора, для каждой точки коалесцирующей системы характерна тенденция к равновесию между коалесценцией и дроблением пузырьков так, что в конечном итоге образуются пузырьки с диаметром Dc.
Эти соображения необходимо учитывать при проектировании соответствующих аппаратов. В некоалесцирующей системе рассеяние энергии, расходуемой на диспергирование газа, наиболее эффективно в зонах образования и диспергирования пузырьков. Если же процессы коалесценции играют большую роль, то рассеяние энергии, расходуемой на диспергирование газа, происходит более или менее равномерно во всем объемежидкой фазы. Как мы увидим позднее (гл. 9), эти теоретические выводы послужили основой для разработки, изучения и использования перемешивающих и смесительных устройств для биореакторов самых разнообразных конструкций; по этой причине они и некоторые другие выводы качественного характера в настоящее время, возможно, являются наиболее ценными с практической точки зрения результатами рассмотренных выше теоретических работ. Действительно, такие характеристики реакторов, как пространственная неоднородность структуры течений, особенности турбулентных течений, объемные доли газа и жидкой фазы, в большинстве случаев настолько сложны, что их количественная оценка расчетным путем крайне затруднена и получить необходимые численные данные обычно удается только с помощью эмпирических уравнений. При выборе последних, однако, мы не должны забывать только что рассмотренную физическую основу явлений. Так, уравнение, описывающее коалесцирующую систему чистый воздух — вода, вероятнее всего, будет неприменимо к процессу, в котором участвует относительно некоалесцирующая двухфазная система.
Теперь, возвращаясь к параметрам уравнения (8.39), определяющего площадь поверхности раздела фаз в единице объема а', рассмотрим время пребывания пузырьков tb в реакторе. Этот параметр можно найти путем интегрирования скорости подъема пузырька по высоте реактора hr:
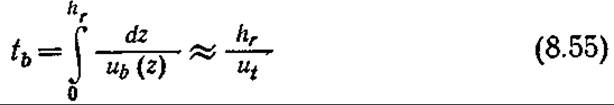
Здесь в правом выражении приближенно принято, что скорость подъема пузырька равна его конечной скорости. В случае отдельных мелких пузырьков при небольших числах Рейнольдса конечную скорость можно определить, воспользовавшись уравнением (8.32). Если же речь идет о больших сферических или полусферических пузырьках диаметром D в ньютоновской жидкости, то в соответствующих расчетах следует использовать значение конечной скорости, определяемое уравнением
![]()
Расчет характерной скорости движения пузырьков в потоке более сложен, поскольку, во-первых, одни пузырьки влияют на движение соседних и, во-вторых, в процессе движения пузырьки могут коалесцировать или распадаться на более мелкие пузырьки. Сравнивая уравнения (8.33) и (8.35), можно видеть, что для идентичных Sc и Sh в первом приближении
![]()
и, следовательно,
![]()
Для любой реальной дисперсной системы характерно то или иное распределение пузырьков по размерам. В связи с этим возникает проблема определения характерного или среднего размера пузырьков. В уравнениях (8.35) — (8.38) под диаметром пузырька D подразумевается усредненный по поверхности диаметр или средний диаметр по Заутеру Dsm:
![]()
Здесь mj — число пузырьков диаметром Dj.
Входящее в уравнение (8.39) выражение nF0tb отражает общий объем пузырьков в реакторе. Отношение объема всех пузырьков к объему реактора (объема газа к объему реактора) называют газосодержанием H. Если величина H известна из других лабораторных или заводских данных или из литературных источников (пример 8.1), то ее можно подставить в уравнение
![]()
В расчетах с привлечением уравнения материального баланса только жидкой фазы, например в уравнениях (8.14) и (8.15), удобнее пользоваться параметром а', представляющим собой отношение площади поверхности раздела фаз к объему жидкой фазы, а также параметром а — отношением площади поверхности раздела фаз к общему объему реакционной смеси (жидкость+газ). Эти два параметра, определяющие величину межфазной поверхности, связаны через газосодержание H:
а'(1—H) = а (8.61)
Будьте внимательны при использовании опубликованных в литературе уравнений массопередачи; проверьте, какой параметр применялся в оригинальной работе — kla или kld'.
Пример 8.1. Эмпирические уравнения для определения газосодержания.
Барботажная колонна*:
H/(1 — H)4 = 0,20(Во)1/8(Gа)1/12Fr (8П1.1)
где Во — число Бонда (Bo = gdt2pc/σ); Ga — число Галилея (Ga = gdt3/uc2); Fr — число Фруда
![]()
uG— поверхностная скорость газа; dt— диаметр колонны (реактора).
* Chakravarty М., Begum S., Singh H. D., Barrah J. N., Iyengar M. S., Biotech. Bioeng. Symp., 4, 373 (1973).
Лабораторная газлифтная колонна*:
Газосодержание в трубе подачи газа (с барботером):
![]()
Газосодержание в кольцеобразном зазоре:
![]()
Газосодержание над отражательной перегородкой;
Н3 =7,5∙10-3u0,88 (8П1.4)
Общее газосодержание колонны:
H = 0,003u0,88
Здесь μl — вязкость жидкой фазы при температуре колонны, сП; μн2о — вязкость воды при температуре колонны, сП; σ — поверхностное натяжение на границе раздела фаз газ — жидкость, дин/см; u — поверхностная скорость газа, см/с; Aіnt — площадь сечения трубы подачи газа, см2; Aаnn — площадь сечения кольцеобразного зазора, см2.
Лабораторная газлифтная колонна**
В трубе подачи газа:
![]()
где ud — поверхностная скорость газа в трубе подачи;

Реактор с перемешиванием***
При условии, что диаметр реактора приблизительно равен высоте и Rei0,7 (NiDi/u)0,3 < 2∙104,
![]()
При Rei0,7 (NiDi/u)0,3 > 2∙104
![]()
и
![]()
где a0, a1 — площадь поверхности раздела фаз в единице объема культуры; Rei — число Рейнольдса мешалки (Rei = pNiDi2/μc); u — поверхностная скорость газа (для незаполненного реактора); ut — скорость подъема пузырьков. Смысл символов Ni, Di, Р, р, σ расшифрован в тексте (см. разд. 8.4). Реакторы с перемешиванием*
Для системы вода — воздух данные могут быть выражены уравнением
![]()
где Р — мощность в л. с.; V — объем жидкой фазы без учета газа, м3; и — поверхностная скорость, м/ч; Н — объемная доля газовой фазы (при 0,02 < H < 0,2).
* Chakravarty М., Begum S., Singh H. D., Barrah J. N., Iyengar M. S., Biotech. Bioeng. Symp., 4, 373 (1973).
** Hatch R. T., Ph. D. Thesis in Food Science and Nutrition, p. 150, Masse» chusetts Institute of Technology, Cambridge, Mass., 1973.
*** Calderbank P. H., Trans. Inst. Chem. Eng., 36, 443 (1958).