Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Процессы переноса в биотехнологических системах
Массообмен через свободные поверхности
Перенос газов через свободные поверхности систем газ — жидкость (рис. 8.10) играет большую роль в обеспечении кислородом культур клеток животных и в удалении из них CО2. Поверхностный массообмен важен также при росте культур во встряхиваемых сосудах и в небольших перемешиваемых биореакторах, предназначенных для культивирования микроорганизмов. Перенос газов через свободную поверхность жидкости существенен для реаэрации естественных водных потоков и для дыхания аэробных организмов в приповерхностных слоях морей и озерных биоценозах. Массообмен через свободные поверхности жидкостей играет большую роль в различных микробиологических процессах в слоевых реакторах со струйным течением жидкости, применяющихся, в частности, в производстве винного уксуса и обработке сточных вод. В перечисленных случаях глубина проникновения кислорода зависит от масштаба вихрей вблизи поверхности жидкости. Много работ посвящено изучению массообмена с участием стекающей пленки жидкости, хотя далеко не все полученные результаты применимы в микробиологических процессах. Массообмен в стекающих пленках жидкостей мы и рассмотрим в первую очередь.
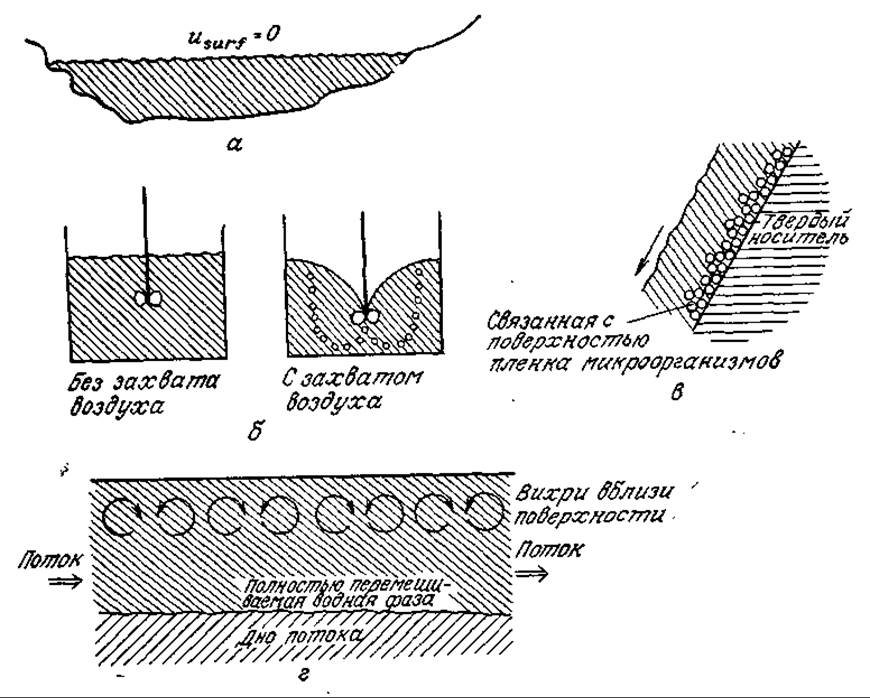
РИС. 8.10. Различные способы массообмена через свободные поверхности: а — неподвижная поверхность (спокойное озеро); б — реакторы с перемешиванием; в — стекающая пленка; г — турбулентный водный поток.
Для стекающей пленки жидкости с толщиной h, длиной L и шириной W при нулевой начальной концентрации растворенного газа интегрированная по площади скорость абсорбции газа выражается уравнением

где umax — скорость свободной поверхности. При выводе этого уравнения допускалось, что концентрация растворенного газа вблизи твердой поверхности всегда равна нулю; иными словами, за время стекания пленки растворенное вещество не успевает проникнуть в пленку на всю ее толщину [5].
В этом случае число Рейнольдса определяется как
![]()
где роль масштаба длины играет гидравлический радиус Rh:
![]()
Из определения коэффициента массоотдачи следует:
Общая скорость абсорбции = kl(cl* → cl)WL (8.84)
Если cl намного меньше cl* (cl ≈ 0), то уравнения (8.83) и (8.84) можно записать в форме Sh = f (Sc, Re):
![]()
Здесь h — масштаб длины для числа Шервуда и b = (L/h)1/2. Таким образом, Sh пропорционально Re1/2.
Ливански и другие изучали абсорбцию СО2 жидкими пленками, стекающими по наклонной поверхности известной площади; в качестве абсорбирующих жидкостей использовали воду, суспензии водорослей и питательные среды [18]. Для всех трех систем значение kl при Re = (7—8) ∙ 103 было одинаково; при различных числах Рейнольдса изучали только суспензии водорослей, для которых турбулентный режим течения наиболее вероятен. Полученные результаты можно описать уравнением
kl = 4 ∙ 10-5Re2/3 при 2000 ≤ Re ≤ 8000
В турбулентных водных потоках большое значение приобретает масштаб циркулирующих вихрей, поскольку именно он определяет толщину слоя, в который вода переносит свежие порции почти насыщенного раствора газа с поверхности в жидкую фазу. Если мы представим себе изображенный на рис. 8.11 циркулирующий вихрь длиной и глубиной А, то среднее число Шервуда для массообмена в турбулентном режиме по аналогии с уравнением (8.28) можно определить так:
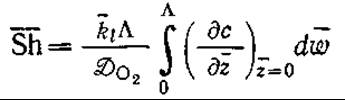
где ![]() — безразмерные координаты, выраженные в масштабе
— безразмерные координаты, выраженные в масштабе ![]() — усредненное по длине вихря значение коэффициента.
— усредненное по длине вихря значение коэффициента.
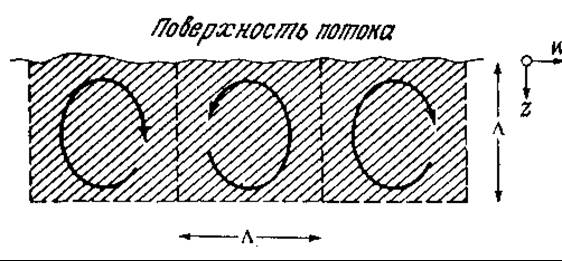
РИС. 8.11. Схема вихрей, циркулирующих вблизи свободной поверхности жидкости.
Скорость массообмена в конечном счете локально зависит от DO2, а также от скорости, с которой жидкость вблизи поверхности обновляется за счет циркуляции. Согласно предложенному одним из первых уравнению Хигби, коэффициент массоотдачи на поверхности системы газ — жидкость в случае одинакового времени пребывания элементов жидкости равен*
![]()
Это уравнение было модифицировано Данквертсом, чтобы его можно было применять при том или ином распределении времени пребывания элементов жидкости на поверхности; оказалось, что и в этом случае kl пропорционально (DO2)1/2. Высказывалось предположение, что время обновления т турбулентного потока равно отношению его глубины h к средней скорости <uw>:
![]()
Отсюда следует, что
![]()
Если ширина потока равна W, то площадь поверхности раздела фаз в единице объема потока составляет
![]()
* Higbie R., Trans. AIChE, 35, 365 (1935).
Таким образом,
![]()
Последнее уравнение довольно успешно применялось для описания скоростей реаэрации обедненных кислородом озер и рек. B другом уравнении учтено изменение kl в зависимости от положения w в вихре:
![]()
Здесь urms — среднеквадратичная скорость циркуляции вихря. В общем случае есть все основания считать ⋀ и urms пропорциональными средней глубине и средней скорости потока соответственно при одном и том же коэффициенте пропорциональности:
![]()
Известно, что на перенос газа в очень большой степени влияет волновое движение на границе раздела фаз вода — воздух. В отличие от рассмотренных выше случаев здесь основными факторами являются параметры течения газа, например средняя и турбулентная компоненты скорости ветра, определяющего характер океанских волн. Эта тема, однако, слишком сложна для настоящего учебного пособия; интересующийся этой проблемой читатель может ознакомиться с ней подробнее в приведенной в конце главы литературе.