Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Процессы переноса в биотехнологических системах
Масштабный переход и массообмен
Как указывал Олдшу, при изменении объема реактора или. скорости вращения мешалки различные параметры, которые могут влиять на произведение kla, изменяются по-разному*.
* Oldshue J., Biotech. Bioeng., 8, 3 (1966).
1. Турбулентное число Рейнольдса Ret определяет urms и, таким образом, коэффициент массоотдачи kl пузырьков:
![]()
2. Окружная скорость лопасти мешалки πNiDi определяет максимальную скорость сдвига у, которая в свою очередь влияет как на максимальный размер устойчивых пузырьков, так и на размер хлопьев скоплений микроорганизмов (разд. 8.3), а также может вызывать повреждения жизнеспособных клеток (разд. 8.8.4).
3. Мощность, расходуемая на единицу объема, P/V через Ret определяет коэффициент массоотдачи и размеры частиц диспергированной фазы. В ламинарном и переходном режимах аэрации, согласно рис. 8.8, б, ![]()
В турбулентном режиме число мощности постоянно, следовательно, ![]()
Тогда, считая объем реактора V пропорциональным Di3, получим
![]()
4. Расход мощности в процессе аэрации равен
![]()
Таким образом,
![]()
Последнее выражение позволяет определить мощность двигателя, необходимую для осуществления данного микробиологического процесса в данном биореакторе.
5. Если содержимое реактора эффективно перемешивается с помощью внутреннего перемешивающего устройства, то система в реакторе должна обладать характерным временем циркуляции. Скорость рециркуляции потока жидкости Flв области перемешивающего устройства изменяется пропорционально площади поперечного сечения πDi2, а средняя скорость мешалки в реакторе пропорционална NiDi. Таким образом,
![]()
Величина Niпредставляет интерес с той точки зрения, что она обратно пропорциональна времени, которое жидкость может провести вне зоны гомогенизирующего действия перемешивающего устройства.
Все перечисленные параметры влияют на ход процесса, и все они по-разному зависят от режима перемешивания. В этой связи возникает вопрос: какой (или какие) из этих параметров должен быть взят за основу при масштабном переходе? Здесь под основой для масштабного перехода мы понимаем простой или сложный количественный параметр, который, будучи справедливым для реактора меньшего объема, может быть без изменения перенесен и на реакторы большего объема. Например, если в качестве условия масштабного перехода мы выберем постоянный расход мощности на единицу объема, то при механическом перемешивании в турбулентном режиме это будет означать, что
![]()
Здесь индексы 1 и 2 обозначают параметры в небольшом и большом реакторах соответственно. В ранних работах по изучению промышленных способов получения пенициллина в качестве условия масштабного перехода биореакторов принимался постоянный расход мощности на единицу объема (около 1 л. с. на 379 л) при сходной конструкции большого и малого реакторов. Как показано на рис. 8.15, а, такое условие масштабного перехода обеспечивает достаточно постоянный выход пенициллина в реакторах емкостью от 5 до 757 л. В то же время изменение величины P/V приводит к тому, что выход пенициллина колеблется в зависимости от масштаба реактора.
Другим часто используемым условием масштабного перехода является постоянство объемного коэффициента массоотдачи kla. На рис. 8.15,6 представлены кривые зависимости выхода продукта жизнедеятельности бактерий витамина В12 от соответствующих значений klap при различных масштабах. Здесь в сложный параметр klap включено общее давление кислорода, что позволяет учесть увеличение движущей силы переноса кислорода при повышенном давлении, что типично для промышленных биореакторов большого объема. В зависимости выхода витамина В12 от klap достигнута удовлетворительная корреляция, хотя выходы в небольших лабораторных реакторах обычно ниже, чем в промышленных реакторах большого объема. Обратите внимание также на то, что в отличие от рассмотренных ранее ситуаций, когда клеточный рост лимитировался переносом кислорода и возникала необходимость в более высоких величинах kla, на кривой зависимости выхода витамина В12 от klap имеется отчетливый максимум. Это объясняется, по-видимому, тем, что в реакторах различного объема при одном и том же kla другие параметры перемешивания и течения жидкой фазы (например, максимальная скорость сдвига или время циркуляции) в общем случае могут различаться.
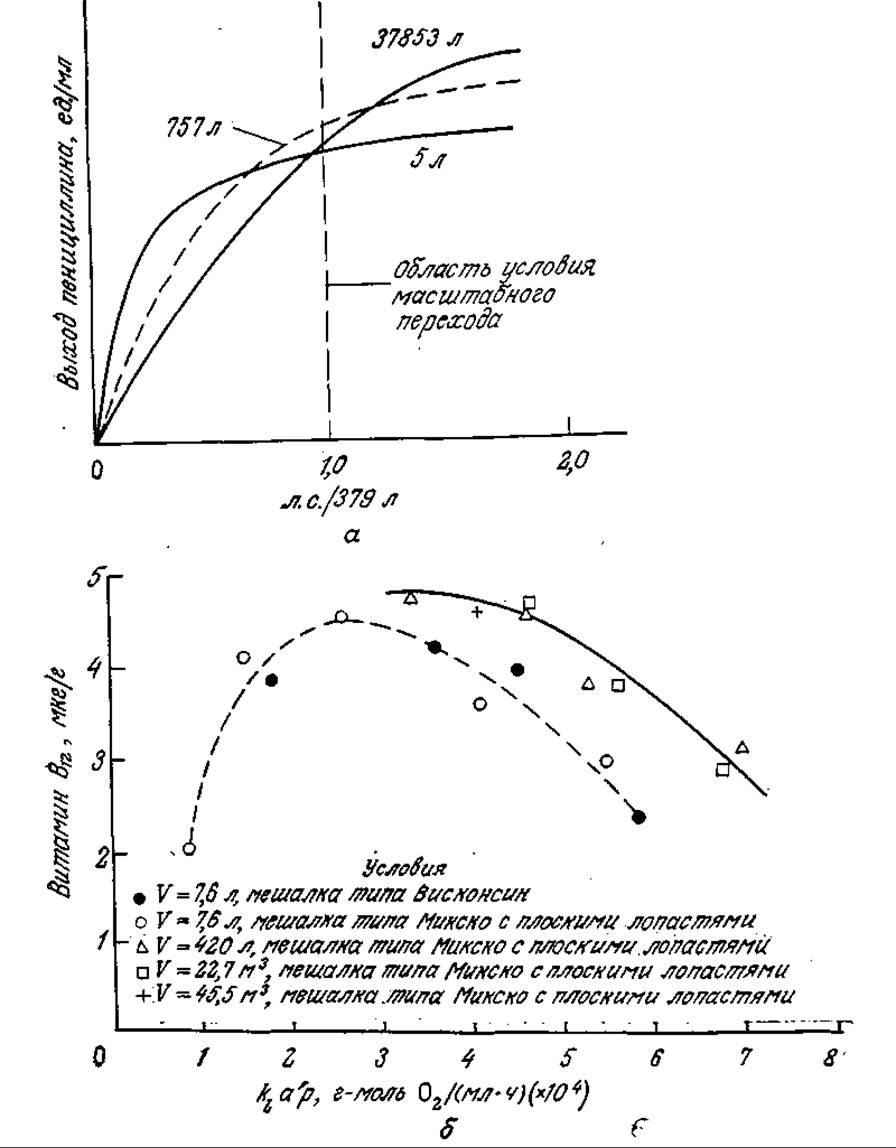
РИС. 8.15. а — зависимость выхода пенициллина от потребляемой мощности в реакторах различного объема [по данным Gaden Е., Sci. Rep. 1st Super, banita, 1, 61 (1961)]; б — зависимость выхода витамина B12(мкг/г) от сложного параметра массопередачи klap (см. текст) [по данным Bartholomew W Н Adv. Appl. Microbiology, 2, 289 (I960).]
Из сказанного следует, что, осуществляя масштабный переход при одном постоянном условии, мы не должны забывать о том, что при этом меняются другие характеристики перемешивания и структура течений. Этот факт особенно наглядно иллюстрируют данные Олдшу, который изучал изменения параметров процесса при увеличении объема биореактора с перемешиванием от 80 до 10000 л*. При таком масштабном переходе Di и V возрастают в 5 и 125 раз соответственно. Величина 1,0 в каждой колонке табл. 8.5 указывает, что данный сложный параметр имеет одно и то же значение и в малом, и в большом реакторе. Значения каждого параметра нормализованы по отношению к 80-литровому реактору, поэтому в столбце «реактор малого объема» все численные значения параметров равны 1,0. Из приведенных в таблице данных следует, что масштабный переход при постоянном P/V сопровождается повышением максимальной скорости сдвига на 70% (NiDi = 1,7), а времени циркуляции — примерно в три раза. С другой стороны, масштабный переход при постоянном времени циркуляции Fl/V требует повышения мощности в большом реакторе в 3125 раз!
Таблица 8.5. Взаимосвязь между различными параметрами при масштабном переходеа
Параметр |
Реактор малого объема (80 л) |
Реактор большого объема (104 л) |
|||
Р |
1,0 |
125 |
3125 |
25 |
0,2 |
P/V |
1,0 |
1,0 |
25 |
0,2 |
0,0016 |
Ni |
1,0 |
0,34 |
1,0 |
0,2 |
0,04 |
Di |
1,0 |
5,0 |
5,0 |
5,0 |
5,0 |
Fl |
1,0 |
42,5 |
125 |
25 |
5,0 |
FlV |
1,0 |
0,34 |
1,0 |
0,2 |
0,04 |
Ni/Di |
1,0 |
1,7 |
5,0 |
1,0 |
0,2 |
Reі |
1,0 |
8,5 |
25 |
5,0 |
1,0 |
а Oldshue S. Y., Fermentation Mixing Scale-up Techniques, Biotech. Bioeng., 8, 3 (1966).
* Oldshue S. Y., Fermentation Mixing Scale-up Techniques, Biotech. Bioeng., 8, 3 (1966).
Различные зависимости важнейших явлений переноса от конструкции перемешивающего устройства приводят к тому, что решение задачи масштабного перехода в случае реакторов с перемешиванием становится своего рода искусством. При этом мы должны стараться выбрать в качестве условия переноса такой параметр, который в данном биопродессе является определяющим. Эта проблема в свою очередь может быть связана с рядом трудностей, обусловленных тем обстоятельством, что явления переноса, зависящие от размеров мешалки и скорости ее вращения, могут непредсказуемым образом влиять на чувствительные к механическим воздействиям клетки.
Общую скорость поглощения кислорода в реакторе находят, исходя из kla и соответствующего описания конструкции реактора. Если жидкая фаза по своему составу гомогенна (однородна) и если пузырьки равномерно распределяются во всем объеме раствора, то скорость массообмена определяется простым выражением:
Vkla(c* — cliq)е = скорость поглощения О2, моль/с (8.111)
Здесь подстрочный индекс е указывает, что в данном случае имеется в виду состав отходящих газов (если мы допустим, что для реактора характерно полное перемешивание, то состав фазы на выходе из реактора не отличается от состава этой фазы в реакторе; гл. 9).
Если в реакторе пузырьки поднимаются в режиме полного вытеснения, но перемешивающее устройство все еще обеспечивает полное перемешивание жидкой фазы, то с* меняется в зависимости от положения пузырька в реакторе. Мгновенная потеря кислорода пузырьком при подъеме последнего на высоту dz составляет

или
![]()
или скорости переноса кислорода из газовой фазы в жидкую. Поскольку pО2 = Mcl* (здесь М — константа в уравнении закона Генри), то
![]()
При постоянной скорости ub подъема пузырьков dt = dz/ubи зависимость с* от z описывается уравнением
![]()
или
![]()
Следовательно, общая скорость массообмена в объеме Ah равна
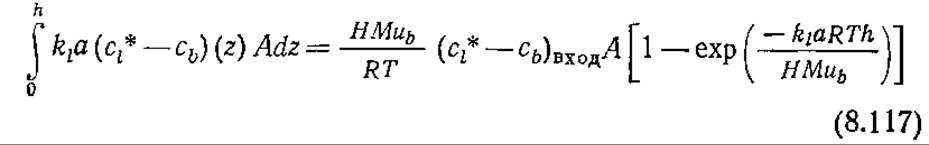
Взаимное влияние перемешивания, кинетики микробиологических процессов и массообмена мы рассмотрим в оставшихся главах этой книги.