Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Процессы переноса в биотехнологических системах
Теплообмен
Уравнения теплообмена

Из уравнения (8.118) и общего теплового баланса [уравнение (8.119)] процессов нагревания, охлаждения и стерилизации следует следующее общее уравнение для расчета теплопередачи:

Чтобы это уравнение можно было использовать в практических расчетах, необходимо найти выражение для определения коэффициента общей теплопередачи h, аналогичное рассмотренным ранее выражениям для коэффициента общей массопередачи в системе газ — жидкость. Условие непрерывности теплового потока требует, чтобы в стационарном состоянии для теплопередачи через плоскую стенку толщиной L_w, разделяющую культуральную жидкость с температурой Т_жидк,1 и нагревающую или охлаждающую жидкость с температурой Т_жидк,2, удовлетворялось уравнение

Здесь k_s — теплопроводность стенки, выраженная в ккал/(см⋅с⋅град). Если в это уравнение ввести коэффициент общей теплопередачи h, определяемый как

то уравнение (8.124) можно преобразовать в

По аналогии с уже изученной нами массопередачей общее сопротивление теплопередаче равно сумме трех сопротивлений. При теплопередаче через цилиндрическую трубчатую поверхность нагревающих или охлаждающих змеевиков площадь поверхности (в поперечном сечении) не остается постоянной, а возрастает пропорционально расстоянию от внутренней поверхности трубы. В такой ситуации уравнение для необходимо модифицировать следующим образом:

Здесь d_iи d₀— наружный и внутренний диаметры трубы соответственно. Обратите внимание на индекс о при коэффициенте указывающий на то, что основой для расчета площади теплопередачи является наружный диаметр трубы. Теплопроводность k_s твердых тел зависит от их природы. Так, при 100 °С k_s равно 0,908 кал/(с⋅см⋅К) для меди и 0,107 кал/(с⋅см⋅К) для стали; при понижении температуры k_s медленно возрастает. Величины k_s для различных материалов, применяющихся в теплообменниках, можно найти в любой технической справочной литературе.

Изучение переноса количества движения и теплоты на любой из границ раздела жидкость — твердое тело позволяет определить соответствующие коэффициенты теплопередачи на границах раздела фаз h_w1, h_w2 или h₀, h_i в уравнениях (8.126) и (8.127) соответственно. Если такие индивидуальные коэффициенты изменяются в зависимости от положения на поверхности теплопередачи, то общий локальный коэффициент теплопередачи определяется уравнениями типа (8.126) и (8.127), а для расчета общего количества передаваемой теплоты необходимо интегрирование по всей поверхности теплопередачи.

При изучении теплопередачи в системе жидкость — твердое тело применяются следующие критерии подобия:

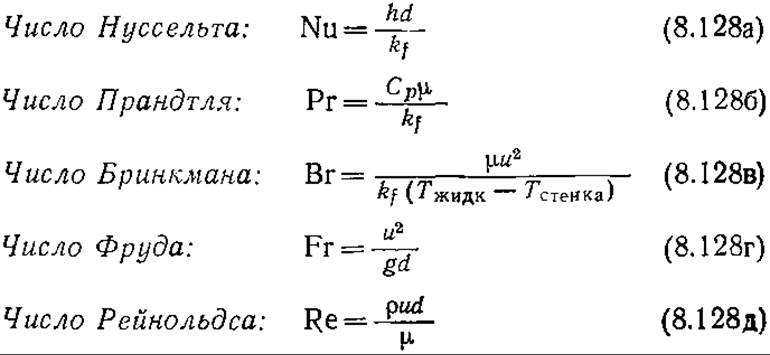
Здесь kf — теплопроводность жидкости, кал/(с⋅см⋅град); С_р — теплоемкость, кал/(г⋅град); d — расстояние (или диаметр трубы), см; μ — вязкость, П; u — скорость, см/с; g — постоянная силы тяжести, г⋅см/с².

Как указано в работе [5], число Бринкмана представляет собой количество теплоты, участвующей в вязком рассеянии, отнесенное к теплопередаче за счет теплопроводности; в наших условиях при теплопередаче через поверхность теплообменника этой величиной можно пренебречь. (Число Бринкмана может быть большим вблизи лопасти мешалки.) Аналогично в реакторах с отражательными перегородками или с мешалкой, смещенной относительно оси реактора, число Фруда обычно пренебрежимо мало.

Коэффициент теплопередачи h, выраженный в виде безразмерного критерия подобия Nu, является функцией от Рr и Re:

Nu = f(Pr, Re)      (8.129а)

При ламинарном течении в прямых трубах теплопередача зависит и от отношения длины трубы L к ее диаметру d (L/d), поэтому предлагались и уравнения типа

Изменение температуры обусловливает изменение различных свойств жидкости вблизи от поверхности теплообмена. Из этих свойств важнейшим является вязкость, поэтому отношение μ_b/μ₀, где μ_b и μ₀ — вязкость жидкости при температуре жидкой фазы и температуре стенки соответственно, также следует учитывать в уравнении:

Так как h (а следовательно, и Nu) можно определять и как локальный коэффициент переноса, и как коэффициент, усредненный по поверхности теплопередачи одним из нескольких способов, то при использовании опубликованных в литературе величин Nu_loc или Nu_av следует применять ∆Т_lос или ∆T_аv соответственно.

Для теплопередачи при турбулентном течении жидкостей, вязкость которых близка вязкости воды, предложено следующее уравнение, полезное как в случае нагревания, так и при охлаждении реакционной массы*:

Это уравнение оказалось справедливым при

10⁴≤ Re ≤ 1,2⋅10⁵ (турбулентный режим)

0,7≤Рr≤120 (для всех жидкостей, кроме расплавленных металлов)

L/d≥60 (длинные трубы)

В модифицированном Сейдером и Тэйтом** виде последнее уравнение применимо и при больших разностях температур; оно оказалось полезным для определения теплопередачи вязкими жидкостями, например маслами:

Если жидкая фаза неоднородна по плотности, то в теплообмен вносит большой вклад и естественная конвекция; в этих случаях в соответствующие уравнения вводят число Грасгофа:

* McAdams W. Н., Heat Transmission, 3d ed., p. 152, McGraw-Hill Book Company, New York, 1954.

** Seider F. E. N.. Tate G. E., Heat Transfer and Pressure Drop of Liquids in Tubes, Ind. Eng. Chem., 28, 1429 (1936).

Тогда уравнение для Nu при течении жидкости в горизонтальных трубах принимает вид*

(В случае вертикальных труб вместо отношения вязкостей применяют коэффициент 1,0, а константу 0,04 заменяют на 0,0722.)

Теплопередача неньютоновскими жидкостями описывается другими уравнениями. Так, для псевдо пластических жидкостей (разд. 8.8) применяли два уравнения**:

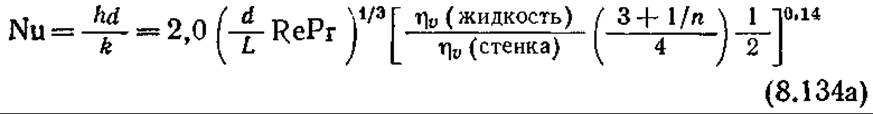
или

Здесь η_v — кажущаяся вязкость [уравнение (8.92)], определенная при температуре жидкой фазы или стенки. Обратите внимание на то, что для ньютоновской жидкости (n = 1) при небольшой разности температур между жидкой фазой и стенкой уравнение (8.1346) сводится к уравнению (8.133). В уравнении (8.134а) изменение вязкости в зависимости от температуры учтено в той же мере, что и в уравнении (8.133).

В принципе теплообменные аппараты могут иметь самые различные поверхности и режимы потоков. Некоторые уравнения для ряда конкретных ситуаций приведены в примере 8.3; другие можно найти в обычных руководствах по теплообмену и в гл. 3 монографии Чарма (ссылка [30] в гл. 9). Ряд примеров расчета коэффициентов теплопередачи и нагрузок теплообменных аппаратов рассмотрен в упражнениях. Иногда культуральная жидкость образует осадок на поверхности нагревателя; это приводит к загрязнению системы, изменению коэффициента теплопередачи стенки во времени и увеличению h со стороны жидкости.

Пример 8.3. Уравнения теплопередачи

Теплопередача естественной конвекцией от вертикальной плоскости или от поверхности цилиндра***:

Здесь L — длина стенки или диаметр цилиндра. Все параметры рассчитаны при (Т_жидк+Т_стенка)/2, а также при

* Martinelli R. С., Boelter L. М., AIChE Mtg., 1942 (цитировано по McAdams W. Н., см. выше).

** Charm S. Е., Merill Е. W., Heat Transfer Coefficients in Straight Tubes for Pseudoplastic Food Materials in Streamline Flow, Food Res., 24, 319 (1959).

*** King W. J., Free Convection, Mech. Eng., 54, 347 (1932).

Теплопередача в пространстве между соосными цилиндрами* Ламинарный режим:

где d₀, d_і — наружный и внутренний диаметры. Турбулентный режим:

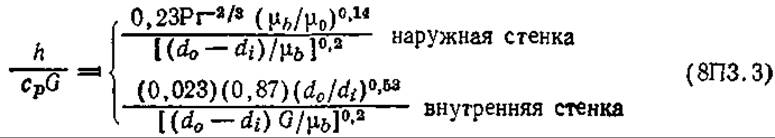
Течение под действием силы тяжести по горизонтальным трубным поверхностям

Здесь w — скорость течения жидкости; L — длина трубы; d₀— наружный диаметр.

Турбулентное течение в трубах***:

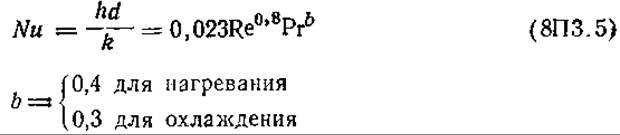
Течение, перпендикулярное изолированному цилиндру***:

Течение, перпендикулярное ряду труб, расположенных на расстоянии двух диаметров одна от другой***:

* Monrad С. С., Pelton J. F., in McAdams W. H., Heat Transmission, McGraw-Hill Book Company, New York, 1954.

** Dittus F. W., Boelter С. M. K., Univ. Calif. Publ. Eng., 2, 443 (1930); (цитировано no McAdams W. H., Heat Transmission, см. выше).

*** Charm S. E., Fundamentals of Food Engineering, 2d ed., Chap. 4, Avi Pwblishing, Westport, Conn., 1971.

Здесь Re_m — Re при u_max, а расстояние 2d определяется следующим образом:

Расположенные в шахматном порядке последовательные ряды труб такого же типа*:

Применяется уравнение (8П3.7), причем коэффициент 0,21 заменяется на 0,27 при 3 рядах, на 0,30 при 5 рядах и на 0,33 при 10 и более рядах труб.

Проблемам массо- и теплообмена посвящено огромное число работ. В настоящей главе мы рассмотрели только основные принципы определения параметров, представляющих наибольший интерес для биохимической технологии. Как указано в некоторых из перечисленных в конце этой главы литературных источников общего характера, к настоящему времени опубликовано очень большое число эмпирических и полуэмпирических уравнений для определения тепло- и массопередачи в самых разных условиях. В практической работе всегда следует использовать уравнения, в наибольшей степени отвечающие изучаемому процессу; кроме того, во всех случаях необходимо учитывать области применимости уравнений.

* Charm S. Е., Fundamentals of Food Engineering, 2d ed., Chap. 4, Avi Publishing Westport, Conn., 1971.