Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Процессы переноса в биотехнологических системах
Стерилизация газов и жидкостей фильтрованием
В предыдущих разделах мы обсуждали стерилизацию жидкостей нагреванием. Однако высокие температуры могут способствовать разрушению некоторых компонентов среды, и, кроме того, тепловая стерилизация газов нецелесообразна по экономическим соображениям. Альтернативным способом стерилизации, пригодным как для газов, так и для жидкостей, является фильтрование, позволяющее с помощью фильтров отделить все нежелательные жизнеспособные клетки, а иногда и вирусы.
Фильтры изготавливаются из пористого фарфора, спрессованного асбестового волокна или из синтетических микропористых полимерных мембран. Первые два материала в настоящее время представляют интерес только с исторической точки зрения; сейчас почти всегда для стерилизации фильтрованием применяют полимерные микропористые мембраны. Такие фильтры широко используются для стерилизации газов (в потоке) или разбавленных жидких суспензий, поступающих в биореактор.
Мембранные фильтры имеют следующие преимущества:
1. Получаемые из устойчивых гелей пористые мембраны имеют чрезвычайно малый разброс пор по диаметрам и благодаря этому обстоятельству эффективно задерживают любые частицы, размер которых превышает определенную величину (контролируемую путем изменения размеров пор).
2. Высокая пористость (часто достигающая 70—80%) и малая толщина (около 100 мкм) обеспечивают низкое сопротивление течению жидкости или газа и тем самым высокую пропускную способность мембранных фильтров по отношению к растворителю (воде). Так, мембрана с фильтрующей поверхностью 10 см2 и порами диаметром 0,2 мкм способна пропускать 1 л жидкости за 2—3 мин.
3. Все фильтрующие материалы мембран (в том числе нитроцеллюлоза, ацетилцеллюлоза, винильные полимеры, полиамиды и фторуглеводороды) выдерживают стерилизацию паром, устойчивы по отношению к большинству водных суспензий и ко многим органическим веществам.
4. Качество мембраны заводского изготовления легко проверяется с помощью суспензии жизнеспособных микроорганизмов, обладающих практически одинаковыми размерами. Например, пористые фильтры с диаметром пор 0,22 мкм проверяют с помощью суспензии бактерий Pseudomonas aeruginosa, а Serratia marcescens может служить эффективным инструментом для проверки мембран с порами диаметром 0,45 мкм. Штаммы вирусов можно применять для контроля фильтров с очень мелкими порами; недостатком этого метода является отсутствие отработанных методик культивирования вирусов.
Рассмотренные в этом разделе фильтры применяют для отделения следовых количеств твердых частиц от газов или жидкостей с целью стерилизации последних (в производстве фармацевтических препаратов) или с целью отделения патогенных организмов (в производстве напитков). Фильтрование как способ выделения твердых тел из концентрированных суспензий, например культуральных жидкостей, мы рассмотрим в гл. 11.
Упражнения
8.1. Коэффициенты диффузии кислорода в растворах белков. Штреве [53] указывал, что предложенное еще в 1881 г. Дж. К. Максвеллом (Treatise on Electricity and Magnetism, vol. 1, 3d ed.) уравнение для диффузии через жидкость, содержащую сферические частицы, упрощается до приведенного ниже выражения, если эти частицы непроницаемы:
![]()
где D — кажущийся коэффициент диффузии в суспензии; D0 — кажущийся коэффициент диффузии в чистой жидкости; f — объемная доля частиц. Он нашел, что указанное уравнение хорошо согласуется с экспериментальными данными, если f = fp + fb, где fр — объемная доля белка, a fb — объемная доля воды, адсорбированной на поверхности молекул белка. Приняв, что молекула белка по своим размерам отвечает гемоглобину (сфероид 65X55X55 А), вычислите D/D0 и начертите график зависимости D/D0 от fp (не от f) при условии, что молекулы белка окружены 0, 1 или 2 монослоями иммобилизованной воды (диапазон fp от 0,1 до 0,5). Сравните полученные вами результаты с приведенными ниже экспериментальными данными для метгемоглобина; обсудите результаты сравнения.
D/D0 |
0,69 |
0,43 |
0,17 |
fp |
0,1 |
0,2 |
0,4 |
8.2. Коэффициент массоотдачи. Определите klдля следующих условий:
объем жидкой фазы 10 л
диаметр турбинной мешалки 10 см
диаметр сосуда 50 см
скорость вращения мешалки 200 оборотов в мин
коэффициент бинарной диффузии воздух — среда 0,5⋅10-5 см2/с
скорость подачи воздуха 2 л/мин
плотность среды 1,2 г/см3
вязкость среды 0,1 г/(см∙с)
8.3. Перенос кислорода в отсутствие перемешивания. Рассмотрим неперемешиваемый аэрируемый хемостат объемом 0,5 л, в дне которого имеется 10 отверстий. Какая удельная скорость роста клеток будет поддерживаться в хемостате, если диаметр каждого отверстия равен 1 мм, скорость подачи воздуха через одно отверстие составляет 5 мл/мин и если кислород лимитирует скорость роста клеток. Коалесценцией и дроблением пузырьков воздуха можно пренебречь; считайте, что среда разбавлена в такой степени, что по своему поведению не отличается от чистой воды. В расчетах примите следующие значения параметров: μmах = 0,5 ч-1; Ks = 0,1 мМ; σ = 72 дин/см; g = 980 см/с2; μгаз = 2⋅10-4 г/(см⋅с); D = 0,5⋅10-5 см2/с; μжидк = 10-2 г/(см⋅с); pгаз = 1,4 г/л; HL = 10 см; YO/X = 1 г O2/г клеток; х = 1,0 г клеток/л.
8.4. «Изменение» kla с температурой. Теория обновления поверхности предусматривает, что коэффициент массоотдачи изменяется пропорционально D1/2. Для случая диффузии в жидкостях, согласно уравнению Стокса — Эйнштейна, Dμ/Т = const. Следовательно, klдолжно быть пропорциональным (Т/μ)1/2.
а) Найдите в любом справочнике данные по зависимости вязкости воды от температуры и вычислите изменение отношения kl(T)/kl(T — 15°С) в диапазоне от 15 до 60° С; изобразите результаты в графической форме.
б) Равновесная концентрация растворенного кислорода зависит от температуры (табл. 8.1). Приняв, что отношение площади поверхности раздела фаз к объему а не зависит от температуры, вычислите изменение y ≡ [klac*(T)/klac*(T = 15°С)] от температуры в том же диапазоне, что и в упражнении 8.4 а; изобразите результаты в графической форме.
Какое, по вашему мнению, практическое значение может иметь показанное в этом упражнении постоянство величины у? Постоянство ч подтверждено экспериментально [54].
8.5. Реактор периодического действия; зависимость клеточного роста от массообмена. Периодическая культура микроорганизмов растет при 35 °С. Методом окисления сульфитом натрия показано, что kla'cl* = 0,1 моль/(л∙ч).
Бремя удвоения численности популяции в периоде экспоненциального роста составляет 30 мин, экономический коэффициент по кислороду равен 0,6 г «леток/г О2.
а) Вычислите удельную скорость клеточного роста μ, в экспоненциальной фазе.
б) С помощью уравнения (8.14) рассчитайте концентрацию растворенного кислорода сl при увеличении клеточной массы (начальное значение x0 = 10-6 г/мл). Постройте график зависимости cl от х. При какой концентрации клеточной массы концентрация clдолжна стать равной нулю?
в) В реальном процессе никогда не становится равной нулю. Вместо этого при низких концентрациях растворенного кислорода μ становится функцией cl, на что указывает, например, уравнение (8.15). С помощью уравнения (8.15) и приведенных выше значений параметров вычислите зависимость сl от x. Примите КO2 равным 0,05 ммоль/л. (Удобнее по заданным величинам cl вычислять х.)
г) При cl>0,9 cl* процесс лимитируется клеточным ростом, а при cl < 0,1 cl* скорость процесса ограничивается массообменом. С помощью уравнения (8.15) и графика, полученного при решении упражнения 8.5в, определите диапазоны значений х, которые соответствуют режимам, лимитируемым ростом и массообменом.
д) Правая часть уравнения (8.15) представляет собой dx/dt. На том же чертеже, на котором вы решили упражнение 8.5в, постройте график зависимости dx/dt от x. Каким выражением определяется х при (dx/dt) max?
8.6. Влияние давления. Перенос кислорода интенсифицируется при повышении его парциального давления путем простой замены воздуха на чистый кислород. Предлагалось также применять повышенное давление. К сожалению, рост микроорганизмов может подавляться кислородом за счет, например, накопления в клетке активных форм кислорода, которые могут подавлять внутриклеточные превращения, нуждающиеся в локальных восстановительных условиях.
а) Допустим, что зависимость скорости клеточного роста от концентрации кислорода можно описать уравнением
![]()
или
![]()
Где ![]()
Покажите, что удельная скорость клеточного роста будет максимальной при ![]()
б) На основе уравнения (8.15), модифицированного путем включения приведенного выше выражения (отражающего ингибирующее действие кислорода), выведите уравнение, которое будет предсказывать давление кислорода рO2, обеспечивающее максимальную скорость роста при любом значении x. Поскольку μmах = const, определите также соответствующую зависимость рO2 от времени.
8.7. Секреция продукта клеточного метаболизма в среду, а) В микробиологическом процессе синтеза L-аспартата последний образуется в концентрации 1, 2, 3 и 4 г/л через 1, 2, 3 и 4 ч после начала процесса соответственно. Если при t = 0 добавить поверхностно-активное вещество (цетилпиридинийхлорид), то концентрация L-аспартата повысится до 12, 22, 30 и 35 г/л соответственно. Можете ли вы объяснить, какой основной процесс (или процессы) лежит в основе накопления L-аспартата в среде в отсутствие и в присутствии поверхностно-активного вещества? (Данные взяты из работы [55].)
б) Накопление аминокислот в среде некоторыми штаммами Е. coli происходит в результате двух одновременно протекающих конкурирующих явлений — пассивного транспорта из клетки и активного транспорта в клетку. Напишите уравнение скорости накопления в среде аминокислоты, если этот процесс определяется двумя указанными явлениями. Опишите ряд методов экспериментального определения начальных скоростей накопления аминокислот; с помощью меченных 14С аминокислот эти методы должны обеспечивать определение всех параметров предложенного вами уравнения скорости процесса.
Мутации, устраняющие катаболитную репрессию и подавляющие активный транспорт, могут привести к тому, что накопление продукта метаболизма будет лимитироваться только его транспортом (см. [56]).
8.8. Мицелий, иммобилизованный на микробусинах. Адсорбция спор штамма Penicillium chrysogenum на пористых частицах диаметром 300— 500 мкм применялась для создания иммобилизованного мицелиального катализатора, характеристики которого ниже сравниваются с характеристиками культуры суспензии мицелия. Обе культуры были выращены в одном и том же биореакторе типа барботажной колонны.
Характеристика |
Суспензия клеток |
Иммобилизованные клетки |
xmax, г/л |
17,0 |
29,0 |
рmах, г/л |
2,0 |
5,5 |
kla∆c, ммолей О2/(л⋅ч⋅атм) |
50—100 |
100—350 |
Базисный параметр — расход мощности, кВт/м3 |
2,3 |
2,3 |
Расход энергии на перенос кислорода, кг O2/кВтч |
0,21 |
0,48 |
Удельный расход энергии, кВтч/г пенициллина G |
0,12 |
0,07 |
а) Приняв (приближенно), что kl пропорционален μ-1/2, оцените отношение вязкостей суспендированной и иммобилизованной культур. Чем, по вашему мнению, обусловлена пониженная вязкость культуральной жидкости с большей концентрацией биомассы?
б) Оцените сравнительную стоимость культуры в суспензии и иммобилизованной культуры. В каком варианте процесс более выгоден с экономической точки зрения [57]?
8.9. Методы масштабного перехода. В табл. 8.5 приведены различные условия масштабного перехода (например, постоянная величина P/V).
а) Проанализируйте положительное (или отрицательное) влияние на другие переменные процесса, если масштабный переход выполняется при постоянстве P/V, Nl, Fl/V, NiDi или Rei.
б) Высказывалось мнение, что масштабный переход лучше всего выполнять при постоянных kla и скорости сдвига жидкости (окружной скорости мешалки), в частности, при Di/Т ≈ 0,25—0,4 и NiDi = 0,5 м/с. С помощью приведенных в этой главе уравнений покажите, как при этих условиях масштабного перехода будут изменяться P/V, Ni, Fl/V и Rei [58].
8.10. Параметры масштабного перехода в процессах аэрации, а) Согласно многим уравнениям, при аэрации с перемешиванием Sh = aReim1Scm2. Покажите, что при одинаковом размере пузырьков одинаковые значения klв двух различных сосудах, например в маленьком (I) и большом (II), возможны только в том случае, если изменение скорости вращения мешалки, выраженной в числе оборотов в минуту Ni, при масштабном переходе описывается
следующим выражением:
![]()
б) Покажите, что из этого уравнения следует приведенное ниже равенство, справедливое при постоянном kl:
![]()
Какой частный вывод следует из последнего уравнения, если принять во внимание рассмотренное в тексте уравнение для турбулентного режима?
в) Если размер пузырьков зависит от параметров перемешивания, какие ограничения налагаются на отношения Ni(II)/Ni(I), (P/V)Ii/(P/V)I?
8.11. Работа барботажной колонны, а) Определите величины а, Н и kl для барботажной колонны при следующих условиях:
скорость подачи газа 20 н. кубических футов (0,566 м3) в минуту скорость подачи жидкой фазы 25 галлонов (94,633 л) в минуту (вода) внутренний диаметр колонны 16 дюймов (40,64 см) средний диаметр пузырьков D 0,25 дюйма (0,64 см) б) Предлагалось иное уравнение для потока пузырьков (массопередача в жидкость или в систему из двух жидкостей) [59]:
![]()
Сравните это уравнение с приведенной в тексте формулой. Еще раз рассчитайте klи оцените разницу (в процентах) между двумя способами определения Sh.
8.12. Реаэрация в естественном водном потоке (быстрины н спокойные участки). Движущийся водный поток приближенно можно описать как чередование глубоких и мелких участков одинаковой ширины. Пусть «глубокие» и «мелкие» участки имеют глубину hD, hs и длину lD, lS соответственно.
а) Определите отношение коэффициентов массопередачи кислорода в глубоких и неглубоких участках.
б) Не подразделяя организмы на отдельные виды, опишите математически процесс утилизации субстрата аэробными организмами в указанной системе из глубоких и мелких участков, считая, что скорость роста ограничивает перенос кислорода. Четко укажите принятые допущения.
в) Найдите математические выражения (при необходимости приняв упрощающие допущения), определяющие долю общего роста микроорганизмов в спокойных участках и долю общего переноса кислорода, осуществляющегося в быстринах.
8.13. Упрощенное описание реаэрации в водном потоке (уравнение Стритера — Фелпса). В условиях, когда осаждение органических веществ, реакции в осадке и потеря органических летучих веществ не играют большой роли, реаэрацию в водном потоке можно описать как простое явление типа потока идеального вытеснения. Уравнение материального баланса по органическому веществу S в потоке, движущемся со скоростью и, можно записать в таком виде:
![]()
Для материального баланса по кислороду предложено уравнение
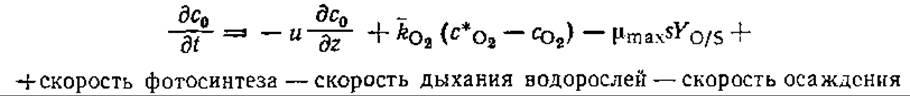
Здесь в правой части уравнения первое слагаемое отражает градиент концентраций кислорода, второе — поступление О2 за счет массообмена, а третье — расход О2 в процессах окисления с участием микроорганизмов,
а) Покажите, что ![]() если микроорганизмы, окисляющие питательные вещества, получают кислород в избытке.
если микроорганизмы, окисляющие питательные вещества, получают кислород в избытке.
б) Покажите, что в стационарном состоянии в отсутствие фотосинтеза, дыхания водорослей и осаждения профиль концентрации кислорода можно описать уравнением Стритера — Фелпса:
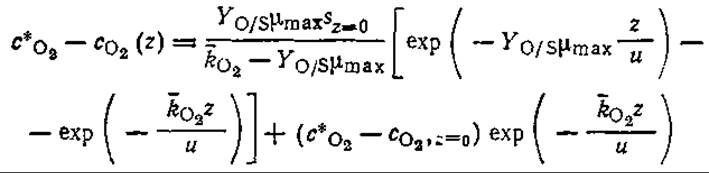
где ![]() — коэффициент массопередачи кислорода, усредненный по вихрю; l — глубина потока.
— коэффициент массопередачи кислорода, усредненный по вихрю; l — глубина потока.
в) Покажите, что в модели Стритера — Фелпса параметр с*O2 — сO2(z), называемый дефицитом кислорода, имеет единственный минимум при
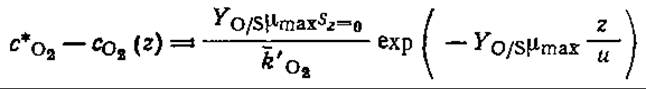
Какое расстояние z соответствует этой точке максимального дефицита кислорода? Выведите аналогичные выражения для случая, когда необходимо учитывать фотосинтез, дыхание водорослей и осаждение, осуществляющиеся с постоянными скоростями.
8.14. Теплообмен; размер пузырьков. Рассмотрим процесс, стехиометрия которого дана в упражнении 5.13.
а) Предположим, что периодический аэробный микробиологический процесс проводится в цилиндрическом резервуаре диаметром 1,83 м, снабженном охлаждающим змеевиком длиной 39,6 м и диаметром 2,54 см, причем расстояние между витками змеевика составляет 3,08 см. Допустим далее, что вся теплопередача осуществляется через змеевики и что барботер поддерживает достаточно высокое значение Kla, при котором рост клеток не лимитируется кислородом. Какой должна быть минимальная, обеспечивающая требуемую теплопередачу скорость вращения мешалки (в оборотах в минуту), если средняя скорость жидкости в направлении, перпендикулярном трубам змеевика, составляет 10% от скорости конца лопасти мешалки, средняя, температура охлаждающей жидкости равна 18 °С и реактор должен работать при температуре не выше 28 °С? Повторите расчеты для концентраций 106, 107, 108 и 109 клеток в миллилитре [диаметр однолопастной мешалки 4,5 фута (1,37 м), толщина лопасти 1,2 дюйма (3,05 см), высота 6 дюймов (15,24 см)].
б) При плотности 109 клеток/мл скорость аэрации такова, что клетки поглощают 10% поступающего кислорода. Из-за неудачной конструкции барботера размер пузырьков слишком велик. Какая скорость мешалки (в оборотах в минуту) необходима для того, чтобы пузырьки имели адекватный диаметр? Не даст ли лучшие результаты установленная непосредственно над. барботером вторая, значительно меньшая, но высокоскоростная лопастная» мешалка, например мешалка с параметрами D2 = 0,2 D1, N2 = 10 N1?
8.15. Критерии подобия. π-Теорема Бэкиигема. В процессах теплопередачи при принудительном течении жидкости по поверхности трубы для определения коэффициента теплопередачи (h) со стороны жидкости важны следующие параметры: характерный диаметр трубы D, скорость течения жидкости u, вязкость жидкости μ (в пуазах), плотность р, удельная теплоемкость при постоянном давлении Ср [в кал/(моль∙град)] и теплопроводность жидкости kf [в кал/(с⋅см⋅град)]. π-Теорема Бакингема устанавливает, что «функциональное соотношение между q величинами, элементы которых представимы в виде комбинаций из р фундаментальных элементов, можно записать, как функцию q—р безразмерных групп». В теплопередаче фундаментальными элементами являются масса т, длина I, время t и температура Т.
а) Выразите h, D, u, μ, р, Ср и k через указанные элементы, т. е, в виде malbtcTd.
б) Четыре безразмерные группы обычно образуются из следующих критериев подобия: Nu (Nu ≡ hD/kf), Re (Re ≡ pDu/μ), Pr (Pr ≡ Cpμ/kf) и числа Стантона St (St = h/uCpp). Выскажите свои соображения. Что, по-вашему мнению, отражает число Стантона?
8.16. Жидкости, подчиняющиеся степенному закону; гидролиз крахмала. Нагревание 1%-ной (масса/объем) суспензии амилопектина в воде приводит к псевдопластичному раствору, который должен подчиняться уравнению т = ηуn, где n < 1,0. При гидролизе этого раствора а-амилазой в реакторе периодического действия наблюдались следующие изменения параметров системы во времени [60]:
η, дин⋅сn/cм2 |
0,32 |
0,26 |
0,20 |
0,14 |
0,10 |
0,03 |
п |
0,73 |
0,75 |
0,78 |
0,83 |
0,85 |
0,98 |
а) Покажите, что эти данные можно описать уравнением т0 = ηу0n, где то, у0 — константы.
б) С помощью соответствующих графиков покажите, что все кривые зависимостей т от у при любой степени гидролиза пересекаются в одной точке.
в) Как будет изменяться во времени потребляемая мощность, если скорость вращения мешалки будет постоянной? Можно ли использовать этот параметр для постоянного неавтономного контроля хода периодического процесса?
8.17. Зависимость потребляемой мощности от скорости вращения перемешивающего устройства в неньютоновских жидкостях. Для неньютоновских жидкостей с показателем степени n < 1 в уравнении степенного закона скорость сдвига y можно считать пропорциональной скорости вращения лопастной мешалки Ni [61].
а) Покажите, что для жидкости, находящейся между двумя соосными цилиндрическими поверхностями, скорость сдвига на внешнем цилиндре (при изменении скорости вращения внутреннего цилиндра) изменяется в соответствии с выражением (dτ/dNi) ∝Nin-1.
б) Покажите, что число Рейнольдса Re = Di2Nip/η0, где ηv — кажущаяся вязкость (зависящая от скорости сдвига), пропорционально Ni2-n.
в) Для указанного выше числа Рейнольдса зависимость числа мощности (Pgc/Di5Ni3p) от числа Рейнольдса совпадает с аналогичной зависимостью для ньютоновских жидкостей (или соответствующая кривая располагается чуть ниже кривой для ньютоновской жидкости). Если Р0 пропорциональна Rea, покажите, что потребляемая мощность пропорциональна Ni3+a(2-n)
г) Как с помощью полученной в предыдущих упражнениях информации вы могли бы определить коэффициент пропорциональности между y и Niдля неньютоновской жидкости?
8.18. Фазы процессов микробиологической переработки углеводородов.
а) На рис. 8.14 изображены основные фазы процесса микробиологической переработки углеводорода по данным Мимуры и др. Найдите математические выражения, описывающие скорости клеточного роста и утилизации субстрата в каждой фазе периодического процесса. Для каждой «фазы» приведите количественные характеристики, определяющие природу основного сопротивления клеточному росту, например растворимость углеводорода, транспорт кислорода, клеточный метаболизм и т. д.
б) Назовите причины, почему система, состоящая из клеток, капелек углеводорода, воздушных пузырьков и растворителя, принимает каждую из упомянутых авторами структур. Какие эксперименты напрашиваются в связи с результатами этих наблюдений? Как вы могли бы доказать предложенные гипотезы или выбрать наиболее обоснованную из них?
8.19. Микробиологические процессы с двумя (газообразными) субстратами. Хэймер и др. [SCP Production from Methane, р. 362 in Single Cell Protein II, Tannenbaum S. R., Wang D. I. C. (eds), MIT Press, Cambridge, Mass., 1975] указывали, что рост клеток при утилизации метана в присутствии кислорода в проточном, постоянно барботируемом реакторе можно описать двойным уравнением Михаэлиса — Ментен:
![]()
здесь индексы 1 и 2 указывают параметры, относящиеся к кислороду и метану соответственно.
а) Допустив, что экономические коэффициенты Y1 и Y2 (г клеток из г субстрата i; i = 1,2) постоянны, напишите уравнения материального баланса по биомассе и субстратам 1 и 2 в стационарном состоянии при условии стерильности питательных веществ. Коэффициент общей массопередачи примите равным Кlia, считайте, что как жидкая, так и газовая фазы полностью перемешиваются.
б) Повышение скорости разведения в конце концов приводит к вымыванию. Покажите графически или аналитически, что вымывание происходит при D около 0,72 ч-1 при следующих значениях параметров: K1 = K2 = 5⋅10-4 г/л; Y1 = 1,25 г клеток/г O2; Y2 = 2,0 г клеток/г субстрата; Кlia = Кl2a = 100 ч-1; cl* = 0,015 г/л; с2* = 0,007 г/л; μmах = 0,8 ч-1.
Литература
Диффузия:
1. Weisz Р., Diffusion and Chemical Transformation: An Interdisciplinary Excursion, Science, 179, 433 (1973).
Потребность культур клеток в кислороде и растворимость кислорода:
2. Finn R. К., Agitation and Aeration, in Biological Engineering Science, Blakebrough N. (ed.), vol. 1, p. 69, Academic Press, Inc., New York, 1967.
Взаимосвязь между диффузией через жидкие пленки и химическими реакциями:
Процессы переноса в биотехнологических системах
3. Данквертс П. В., Газо-жидкостные реакции. — М.: Химия, 1973.
4. Астарита Дж., Массопередача с химической реакцией. — Л.: Химия, 1971.
5. Берд Р., Стьюарт В., Лайтфут Е., Явления переноса. — М.: Химия, 1974.
Культуральные жидкости:
6. Taguchi Н., The Nature of Fermentation Fluids, Adv. Biochem. Eng., 1 (1971).
Проблемы масштабного перехода в микробиологических процессах:
7. Biotech. Bioeng., 8 (1966), Gaden Е. L., Jr. (ed.) (весь том).
Примеры массообмена в микробиологических реакторах:
8. Moser A., in Proc. Int. Symp. Adv. Microb. Eng., 1, 295—580 (1973).
9. Van’t Riet К., Trends in Biotechnology, Mass Transfer in Fermentation, 1, (4), 113 (1983).
Уравнения для определения переноса кислорода:
10. Calderbank Р. Н., Moo-Young М., The Continuous Phase Heat and Mass Transfer Properties of Dispersion, Chem. Eng. Sci., 16, 39 (1961).
11. Calderbank P. H., Mass Transfer in Fermentation Equipment, in Biochemical and Biological Engineering Science, Blakebrough N. (ed.), vol. 1, Academic Press Inc., New York, 1967.
12. Akita КYoshida F., Bubble Size, Interfacial Area, and Liquid-Phase Mass Transfer Coefficient in Bubble Columns, I & EC Process Des. Develop., 13, 84 (1974).
13. Bello R. A., Robinson C. W., Moo-Young M., Mass Transfer and Liquid Mixing in External Circulating Loop Contactors, Adv. Biotech., 1, 547 (1981).
14. Wang К. B., Fan L. T., Mass Transfer in Bubble Columns Packed with Motionless Mixers, Chem. Eng. Sci., 33, 945 (1978).
Потребность в кислороде в периодических процессах:
15. Darby R. Т., Goddard D. R., Studies of the Respiration of the Mycelium of the Fungus Myrothecoum verracaria, A. J. Bot., 37, 379 (1950).
Определение kla с помощью кислородного электрода:
16. Weman W. C., Wilke C. R., New Method for Evaluation of Dissolved Oxygen Response for КLa Determination, Biotech. Bioeng., 15, 571 (1973).
Абсорбция водными пленками:
17. Briffaud J., Engasser M., Growth and Excretion Kinetics in a Trickle-Flow Fermentor, Biotech. Bioeng., 21, 2093 (1979).
18. Livansky К., Prokes B., Kihrt F., Benes V., Some Problems of CO2 Absorption by Algae Suspensions, Biotech. Bioeng. Symp., 4, p. 513 (1973).
Стехиометрия утилизации метана:
19. Klass D. L., Iandolo J. J., Knabel S. J., Key Process Factors in the Microbial Conversion of Methane to Protein, CEP Symp. Ser., [93], 65, 72 (1969).
Уравнения для определения необходимого диаметра отверстий:
20. van Krevelen D. W., Hoftijzer P. J., Studies of Gas-Bubble Formation: Calculation of Interfacial Area in Bubble Contactors, Chem. Eng. Prog., 46, 29 (1950).
21. Schügerl К., Lücke J., Bubble Column Bioreactors, in Advances in Biochemical Engineering, Ghose T. K., Fiechter A., Blakebrough N. (eds.), vol. 7, p. 1, Springer-Verlag, Berlin, 1977.
Фотографическое определение a, H, D Заутера:
22. Calderbank P. H., Rennie J., Int. Symp. Distill. (Inst. Chem. Eng.), 1960.
Зависимость формы больших пузырьков от скорости [уравнение (8.36)]:
23. Davies R. М., Taylor G. I., Proc. Roy. Soc., A200, 375 (1956).
Массопередача через свободную поверхность к стекающей пленке жидкости (см. работу [5]).
Массопередача через свободную поверхность к турбулентному водному потоку:
24. Fortescue G. Е., Pearson J. R. A., On Gas Absorption into a Turbulent Liquid, Chem. Eng. Sci., 22, 1163 (1967).
25. O’Connor D. J., Dobbins W., The Mechanism of Reaeration In Natural Streams, J. Sanit. Eng. Div., Proc. ASCE, 82, SA6 (1966).
Зависимость мощности турбины от Re перемешивающего устройства:
26. Rushton J. Н., Costich Е. W., Everett H. J., Power Characteristics of Mixing Impellers, pt. 2, Chem. Eng. Prog., 46, 467 (1950).
Потребляемая мощность в аэрируемых и неаэрируемых процессах:
27. Ohyama Y., Endoh К., Power Characteristics of Gas-Liquid Contacting Mixers, Chem. Eng. Japan, 19, 2 (1955).
28. Michel B. J., Miller S. A., Power Requirements of Gas-Liquid Agitated Systems, AIChE J., 8, 262 (1962).
Перемешивание с помощью струи жидкости:
29. Blenke H., Loop Reactors, in Advances in Biochemical Engineering, Ghose T. K., Fiechter A., Blakebrough N. (eds.), vol. 13, p. 121, Springer-Verlag, Berlin, 1979.
Литературу по уравнениям с числом Вебера см. в работе [И].
Коэффициенты диффузии кислорода в пленках микроорганизмов:
30. Matson J. V., Characklis W. G., Oxygen Diffusion through Microbial Aggregates, 77th AIChE Meet., Pittsburgh, June 1973.
Влияние ионной силы на kla:
31. Robinson C. W., Wilke C. R., Oxygen Absorption in Stirred Tanks: A Correlation for Ionic Strength, Biotech. Bioeng., 15, 755 (1973).
Поверхностно-активные вещества и массообмен:
32. Eckenfelder W. W., Jr., Barnhart E. L., The Effect of Organic Substances on the Transfer of Oxygen from Air Bubbles into Water, AIChE J., 7, 631 (1961).
33. Benedek A., Heideger W. J., Effect of Additives on Mass Transfer in Turbine Aeration, Biotech. Bioeng., 13, 663 (1971).
34. Bull D. N., Kempe L. L, Influence of Surface Active Agents on Oxygen Absorption to the Free Interface in a Stirred Fermentor, Biotech. Bioeng., 13, 529 (1971).
35. Aida S., Toda K., The Effect of Surface Active Agents on Oxygen Absorption in Bubble Aeration I, J. Gen. Appl. Microbiol., 7, 100 (1963).
36. Mancy K. H., Okun D. A., Effect of Surface Active Agents on the Rate of Oxygen Transfer, Adv. Biol. Waste Treat., IІІ (1963); см. также работы МакКеоуна и Окуна, Тимсона и Данна, а также Карбера в этом же источнике.
Реология микробных бульонов:
37. Leduy A., Marson A. A., Corpal В., A Study of the Rheological Properties of a Non-Newtonian Fermentation Broth, Biotech. Bioeng., 16, 61 (1974). (Изучение культуры A. pullulans.)
38. Roels J. A., van den Berg J., Voncken R. AT., The Rheology of Mycelial Broths, Biotech. Bioeng., 16, 181 (1974). (Изучение культуры Penicillium.)
39. Thompson N., Ollis D. F., Evolution of Power Law Parameters for Xanthan and Pullulan Batch Fermentations, Biotech. Bioeng., 22, 875 (1980).
40. Chang H. T., Ollis D. F., Generalized Power Law for Polysaccharide Solutions, Biotech. Bioeng., 24, 2309 (1982).
Изучение морфологии в связанных последовательно реакторах:
41. Vrana D., Some Morphological and Physiological Properties of Candida utilis Growing «Hypertrophically» in Excess of Substrate in a Two-Stage Continuous Cultivation, Biotech. Bioeng. Symp., 4, 161 (1973).
Определение потребляемой мощности в неньютоновских биологических средах:
42. Taguchi Н., Miyamoto S., Power Requirement in Non-Newtonian Fermentation Broth, Biotech. Bioeng., 8, 43 (1966).
Концентрация клеток и массообмен:
43. Brierley М. R., Steel R., Agitation-Aeration in Submerged Fermentation, pt. 2: Effect of Solid Dispersed Phase on Oxygen Absorption in a Fermentor, Appl. Microbiol., 7, 57 (1959). (A. niger.)
44. Andrews G. F., Fonia J. P., Marrota E., Stroeve P., The Effects of Cells on Oxygen Transfer Coefficients, Chem. Eng. J., 29, B39, B47 (1984).
Перемешивание и повреждение клеток. См. работу [7], а также:
45. Midler М., Finn R. К, A Model System for Evaluating Shear in the Design of Stirred Fermentors, Biotech. Bioeng., 8, 71 (1966).
Суспензии целлюлозной пульпы:
46. Blakebrough N., Sambamurthy K, Mass Transfer and Mixing Rates in Fermentation Vessels, Biotech. Bioeng., 8, 25 (1966).
Фильтрование через волокнистые фильтры:
47. Friedlander S. К., Aerosol Filtration by Fibrous Filters, in Biochemical and Biochemical Engineering Science, Blakebrough N. (ed.), vol. 1, p. 49,. Academic Press, New York, 1967.
48. Air Filtration, Davies C. N. (ed.), Academic Press, New York, 1973.
Фильтрование через мембраны:
49. Dwyer J. L, Filtration in the Food, Beverage, and Pharmaceutical Industries, p. 121, in Filtration: Principles and Practices, Part II, Marcel Dekker, New York, 1979.
Теплопередача; анализ параметров; см. стр. 396 и далее в работе [5], а также:
50. Brown А. I., Macro S. М., Introduction to Heat Transfer, pp. 85—95, McGraw-Hill Book Company, New York, 1958.
Экономические проблемы теплопередачи в микробиологических процессах:
51. Abbott В. Clamen A., The Relationships of Substrate. Growth Rate, and Maintenance Coefficient to Single Cell Protein Production; Biotech. Bioeng., 15, 117 (1973).
Баланс энтальпии в микробиологических процессах:
52. Cooney С. L, Wang D. I. С., Mateles R. I., Measurement of Heat Evolution and Correlation with Oxygen Consumption during Microbial Growth, Biotech. Bioeng., 11, 269 (1968).
Упражнения:
53. Stroeve P., On the Diffusion of Gases in Protein Solutions, Ind. Eng. Chem, Fundam., 14, 140 (1975).
54. Aiba S., Koizumi J., Ru J. S., Mukhopadhyay S. N., The Effect of Temperature on kla in Thermophilic Cultivation of Bacillus stearothermophilus, Biotech. Bioeng., 26, 1136 (1984).
55. Fukui C., Ishida, Microbial Production of Amino Acids, Kodansha Ltd., Tokyo and John Wiley, New York, 1972.
56. Rancourt D. E., Stephenson J. T., Vickell G. A., Wood J. M., Proline Excretion by Escherichia coli K12, Biotech. Bioeng., 26, 74 (1984).
57. Gbewonyo К., Wang D. I. C., Enhancing Gas-Liquid Mass Transfer Rates in Non-Newtonian Fermentations by Confining Mycelial Growth to Microbeads in a Bubble Column, Biotech. Bioeng., 25, 2873 (1983).
58. Oldshue J., Fermentation. Mixing Scale-Up Techniques, Biotech. Bioeng., 8, 3 (1966).
59. Hughmark G. A., Holdup and Mass Transfer in Bubble Columns, Ind. Eng. Chem. Process Des. Dev., 6, 218 (1967).
60. Cruz A., Kinetics and Shear Viscosity of Enzyme Hydrolysed Starch Pastes, Ph. D. thesis, Princeton University, Princeton, N.J., 1976.
61. Metzner A. B« Feehs R. H., Ramos H. L., Otto R. E., Tuthill J. D., Agitation of Viscous Newtonian and Non-Newtonian Fluids, AIChE J., 7, 3 (1961).