Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Кинетика катализируемых ферментами реакций
Кинетика простых ферментативных реакций с одним и двумя субстратами
Кинетика обратимых реакций, реакций с двумя субстратами и с активацией фермента кофактором
Равновесие многих катализируемых ферментами реакций, например реакций гидролиза биополимеров, сильно смещено в сторону продуктов реакции, поэтому, как правило, такие превращения можно считать необратимыми. В других случаях, например при изомеризации глюкозы во фруктозу под действием фермента глюкозоизомеразы, может установиться равновесное состояние, требующее учета вклада обратной реакции. В качестве простейшей модели обратимой ферментативной реакции рассмотрим кинетику последовательных превращений типа
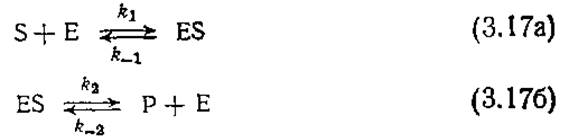
Эта последовательность элементарных реакций отличается от последовательности реакций, предложенных Анри — Михаэлисом — Ментен и выражаемых уравнениями (3.4), только тем, что уравнение (3.176) теперь предусматривает образование комплекса ES из продукта реакции и свободного фермента.
Таблица 3.4. Кинетические параметры некоторых ферментативных реакцийa
Фермент |
Субстрат |
Температура, °С |
pH |
k2,c-1 |
1/Кm, М-1 |
Пепсин |
Этиловый эфир карбобензокси-L-глутамил-L-тирозина |
31,6 |
4,0 |
0,00108 |
530 |
Карбобензокси-L-глутамил-L-тирозин |
31,6 |
4,0 |
0,00141 |
560 |
|
Трипсин |
Бензоил-L-аргининамид |
25,5 |
7,8 |
27,0 |
480 |
Химотрипсиноген |
19,6 |
7,5 |
2900 |
<770 |
|
Стурин |
24,5 |
7,5 |
13100 |
400 |
|
|
Химотрипсин |
Эфир бензоил-L-аргинина |
25,0 |
8,0 |
26,7 |
12 500 |
Метилгидроциннамат |
25,0 |
7,8 |
0,026 |
256 |
|
Метиловый эфир dl-а-хлор-β-енилпропионовой кислоты |
25,0 |
7,8 |
0,135 |
83,3 |
|
Метиловый эфир d-ß-фенилмолочной кислоты |
25,0 |
7,8 |
0,139 |
28,6 |
|
Метиловый эфир l-ß-фенилмолочной кислоты |
25,0 |
7,8 |
1,38 |
100 |
|
Метиловый эфир бензоил-L-фенилаланина |
25,0 |
7,8 |
51,0 |
217 |
|
Этиловый эфир ацетил-L-триптофана |
25,0 |
7,8 |
30,7 |
588 |
|
Этиловый эфир ацетил-L-тирозина |
25,0 |
7,8 |
193,0 |
31,2 |
|
Этиловый эфир бензоил-L-о-нитротирозина |
25,0 |
7,8 |
3,27 |
90,9 |
|
Этиловый эфир бензоил-L-тирозина |
25,0 |
7,8 |
78,0 |
250 |
|
Этиловый эфир бензоил-L-фенилаланина |
25,0 |
7,8 |
37,4 |
167 |
|
Этиловый эфир бензоил-L-метионина |
25,0 |
7,8 |
0,77 |
1250 |
|
Бензоил-L-тирозинамид |
25,0 |
7,8 |
0,625 |
23,8 |
|
Ацетил-L-тирозинамид |
25,0 |
7,8 |
0,279 |
12,3 |
|
Карбоксипептидаза |
Карбобензоксиглицин-L-триптофан |
25,0 /25,0 |
7,5/8,2 |
89/94 |
196/164 |
Карбобензоксиглицил-L-фенилаланин |
25,0 |
7,5 |
181 |
154 |
|
Аденозинтрифосфатаза |
Карбобензоксиглицил-L-лейцин АТР |
25,0/25,0 |
7,5/7,0 |
10,6/104 |
37/79 000 |
Уреаза |
Мочевина |
20,8/20,8 |
7,1/8,0 |
20 000/30 800 |
250/256 |
а Воспроизведено из работы: Laidler К. The Chemical Kinetics of Enzyme Action, p. 67, Oxford University Press, London, 1958.
Как и ранее, будем считать, что реакционная смесь находится в закрытом сосуде и эффективно перемешивается. Тогда на основе материального баланса различных форм фермента [уравнение (3.7)] с учетом приближения квазистационарного состояния [уравнение (3.8)] легко находим, что
![]()
Здесь vS и Ks аналогичны vmax и Кm в уравнениях (3.10) и (3.11) соответственно, и
![]()
Подавляющее большинство катализируемых ферментами реакций протекает с участием по меньшей мере двух субстратов. В то же время чаще всего одним из субстратов является вода, концентрация которой практически постоянна и обычно в 1000 или более раз превышает концентрации других субстратов. Как мы покажем позднее в этом же разделе, в таких случаях можно считать, что реакция протекает с одним субстратом S, и, следовательно, ее кинетику можно изучать так, как это было описано в предыдущем разделе. Кроме того, описанные ниже кинетические модели иногда могут объяснять и влияние кофакторов на скорости ферментативных реакций.
По всей вероятности, во многих процессах с участием двух субстратов могут образовываться тройные комплексы, в которых фермент одновременно связан с двумя субстратами. В таком случае возможна, например, такая последовательность реакций:

так что
![]()
Как и раньше, строчными буквами мы будем обозначать концентрации, а такими же буквами в скобках — концентрацию одной формы, например фермент-субстратного комплекса. Еcли допустить, что первые четыре реакции (3.20) равновесны, то получим
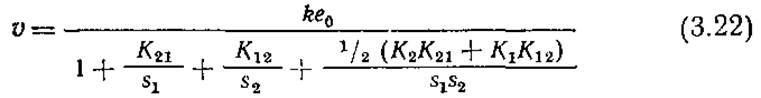
Вывод этого выражения не представляет затруднений, если учесть, что общая концентрация фермента е0 должна быть равна сумме концентраций свободного фермента е и трех комплексов ES1, ES2 и ES1S2. Как и в случае реакций с одним субстратом, в ферментативных реакциях с двумя субстратами можно применить приближение квазиравновесного состояния. В общем случае, однако, в результате получается довольно громоздкое уравнение с таким числом параметров, что оно становится непригодным для практического использования. Удовлетворительное по ряду параметров приближение описывается уравнением (3.22).
Уравнение (3.22) можно далее несколько упростить, если принять во внимание, что условия равновесия требуют, чтобы
К1К12 = К2К21 (3.23)
Соответствующим преобразованием уравнения (3.22) можно прийти к уже знакомой форме уравнений:
![]()
где
![]()
и
![]()
Из последних трех уравнений следует, что если s2 постоянна, s1 изменяется, то реакция будет подчиняться уравнению Михаэлиса — Ментен. В то же время уравнения (3.25) и (3.26) показывают, что кажущиеся максимальная скорость и константа Михаэлиса зависят от концентрации s2.
Если считать приведенные выше последовательность реакций и выражение для скорости реакции с двумя субстратами правильными, то мы можем проверить справедливость уравнения Михаэлиса — Ментен (3.3), допустив, что один субстрат находится в большом избытке. Тогда v*max становится равной ke0, а K1* приближается к постоянному значению K21. Следовательно, реакцию с двумя субстратами при s2 ≫ K2 можно рассматривать как реакцию с одним субстратом.
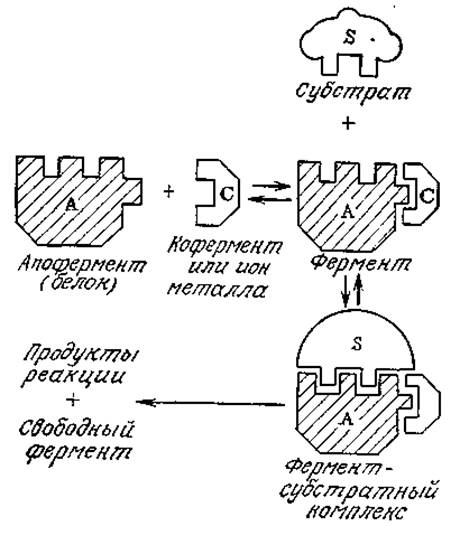
РИС. 3.12. Схематическое изображение предполагаемого механизма ферментативного катализа с участием кофактора.
На рис. 3.12 изображена схема механизма ферментативной реакции с одним субстратом (или с двумя субстратами при s2 ≫ K12) при участии кофактора, которым может быть ион металла или кофермент. Поскольку эта ситуация аналогична только что рассмотренному нами двухсубстратному механизму, здесь нет необходимости снова обращаться к допущению о равновесных последовательных реакциях. Если принять, что субстрат связывается только апофермент-коферментным комплексом, то в конце концов мы получим
![]()
где с — концентрация кофактора. Если считать концентрацию субстрата s постоянной, то это выражение преобразуется в уравнение Михаэлиса — Ментен, отражающее зависимость скорости реакции от концентрации кофактора с. Так, при невысокой концентрации кофактора (с ≪ Kс) реакция будет иметь первый порядок по концентрации кофактора с. С другой стороны, при с ≫ Кс мы получим уравнение скорости реакции с одним субстратом, которая не зависит от концентрации кофактора.
Если S1 и S2 или С и S1 связываются с ферментом в строго определенном порядке, то соответствующее уравнение скорости процесса можно получить, приняв, что Kij запрещенной реакции приближается к бесконечно большой величине.