Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Кинетика катализируемых ферментами реакций
Другие типы зависимостей скорости ферментативной реакции от концентрации субстрата
Активация и ингибирование ферментов субстратами
Скорости не всех катализируемых ферментами реакций подчиняются описанному в разд. 3.2 уравнению Михаэлиса — Ментен. В настоящем разделе мы рассмотрим некоторые наиболее типичные отклонения. Отклонение первого типа, характерное для регуляторных ферментов, можно объяснить связыванием с ферментом нескольких субстратов. Далее мы опишем второй тип отклонений от уравнения Михаэлиса — Ментен, когда субстрат представляет собой смесь различных реагирующих с ферментом веществ, обладающих разными кинетическими свойствами. Анализ отклонений второго типа поможет выявить ряд проблем, с которыми приходится сталкиваться при работе с недостаточно очищенными или плохо охарактеризованными смесями субстратов.
Характерная для некоторых ферментов S-образная форма кривой зависимости скорости реакции от концентрации субстрата свидетельствует об эффекте активации (рис. 3.14). При низких концентрациях субстрата связывание ферментом одной молекулы субстрата повышает скорость связывания следующей молекулы (с математической точки зрения это означает, что на этом этапе реакции dv/ds возрастает). Моделью такого процесса может служить согласованное связывание субстрата субъединицами белка. Предположим, что фермент, например, олигомерной структуры имеет несколько связывающих субстрат центров и что связывание первой молекулы субстрата с ферментом изменяет структуру последнего таким образом, что сродство оставшихся свободными центров по отношению к субстрату увеличивается. Математический анализ такой модели аналогичен рассмотренному в упражнении 2.10 анализу модели гемоглобина, и поэтому мы не будем повторять его в основном тексте.
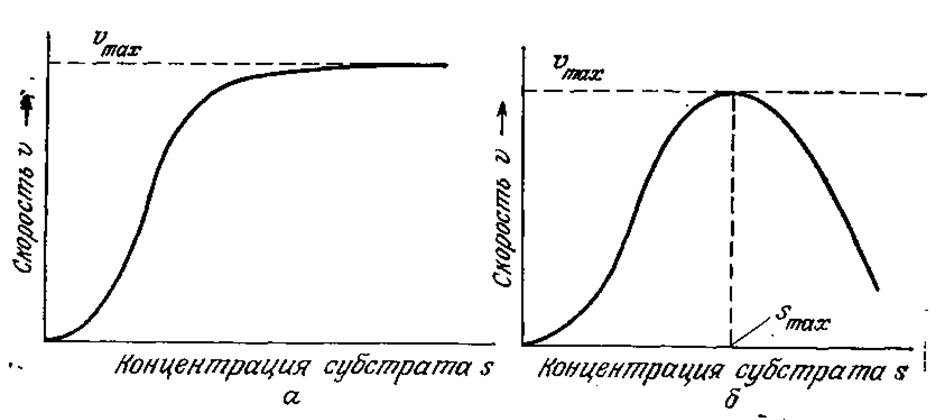
РИС. 3.14. Активация (а) и ингибирование (б) ферментативной реакции субстратом.
Иногда в присутствии большого количества субстрата скорость катализируемой ферментом реакции снижается при повышении концентрации субстрата (рис. 3.15). Это явление называется субстратным ингибированием. Как показано на рис. 3.15, в таких случаях скорость реакции и по мере повышения концентрации субстрата сначала возрастает, затем достигает максимума и, наконец, снижается. Если s больше, чем s, соответствующая vmах, то снижение концентрации субстрата вызывает повышение скорости реакции. Авто каталитический характер реакций такого типа может оказывать существенное влияние на работу биохимических реакторов.
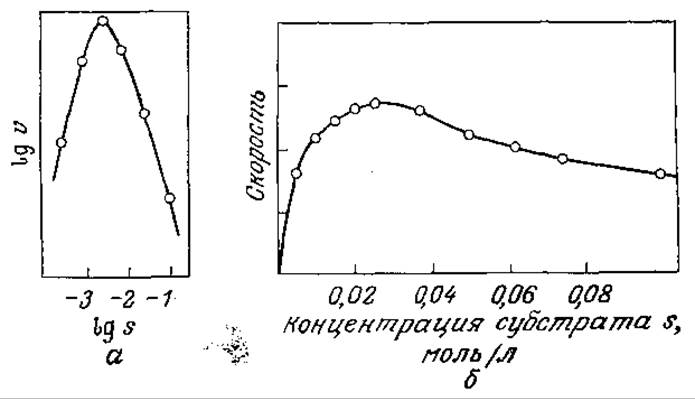
РИС. 3.15. Экспериментальное обнаружение субстратного ингибирования. [Воспроизведено из работы: Laidler К. J., The Chemical Kinetics of Enzyme Action, p. 71, The Clarendon Press, Oxford, 1958. a — данные из статьи: Augustinsson К. D., Substrate Concentration and Specificity of Choline Ester Splitting Enzymes, Arch. Biochem., 23, 111 (1949); б — данные из статьи: Lumry R., Smith E. L., Glantz R. R., Kinetics of Carboxypeptidase Action. I. Effect of Various Extrinsic Factors on Kinetic Parameters, J. Amer. Chem. Soc., 73, 4330 (1951).]
Взаимосвязь между концентрацией субстрата и скоростью ингибируемой субстратом реакции можно оценить количественно с достаточно высокой точностью, используя подход Михаэлиса и Ментен. и допустив, что фермент может связывать и вторую молекулу субстрата, причем в результате присоединения S к ES образуется нереакционноспособное промежуточное соединение. В этом случае в равновесном состоянии будут осуществляться следующие последовательные реакции:
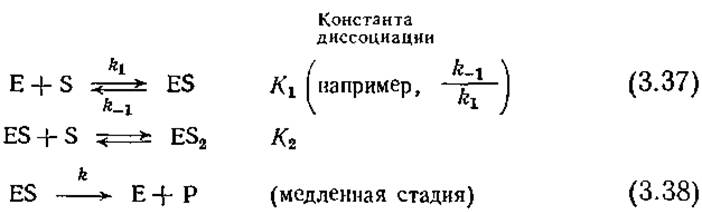
На основе двух указанных равновесных реакций диссоциации с учетом уравнения материального баланса различных состояний фермента, аналогичного уравнению (3.7), после несложных алгебраических преобразований можно получить следующее выражение:
![]()
Экспериментальное определение параметров этого уравнения не вызывает затруднений. Так, сначала путем изменения е0 можно определить k, а затем, построив график зависимости 1/v от s, можно оценить тангенс угла наклона прямого участка кривой, при высоких концентрациях субстрата равный 1/K2ke0 (рис. 3.16). Наконец, K1можно найти по уравнению (3.40); здесь smax удовлетворяет уравнению (3.39) при dv/ds = 0.
![]()