Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Кинетика катализируемых ферментами реакций
Инактивация ферментов
Моделирование и кинетика процессов инактивации
В простейшей модели инактивации молекулы активного фермента (Еа) претерпевают необратимые структурные или химические изменения, приводящие к неактивной форме (Еі):
![]()
Скорость этой реакции rа пропорциональна концентрации активной формы фермента:
rd = kdea (3.76)
Следовательно, в закрытой системе при эффективном перемешивании (примем, что в реакционной смеси нет ни субстрата, ни продукта реакции, ни ингибитора, ни иного эффектора) изменение концентрации активной формы фермента во времени будет описываться уравнением
![]()
так что
![]()
С этим выражением согласуются, в частности, приведенные на рис. 3.27 экспериментальные данные по определению активности аденозинтрифосфатазы в различных условиях. Зависимость константы инактивации kd от температуры может быть описана теорией переходного состояния [например, уравнением (3.72) при а = 1] в форме, несколько отличающейся от уравнения Аррениуса [уравнение (3.66)] для узкого температурного диапазона, представляющего интерес для биологических систем. В табл. 3.10 приведены величины энергии активации Е и энтропии ∆S* для денатурации ряда распространенных ферментов. Как видно из приведенных в таблице данных, для процессов денатурации белков характерны очень большие энергии активации.
В отсутствие ферментативной активности жизнедеятельность клетки невозможна. В некоторых случаях клетка погибает уже после разрушения очень небольшой части внутриклеточных ферментов. В этой связи становится понятным, почему для стерилизации (т. е. для уничтожения всех форм микроорганизмов) газов, жидкостей или твердых тел можно использовать тепловую обработку. В гл. 7 мы узнаем детальнее, почему лишь немногие ферменты (и соответственно немногие микроорганизмы) способны без вреда для себя переносить длительное нагревание.
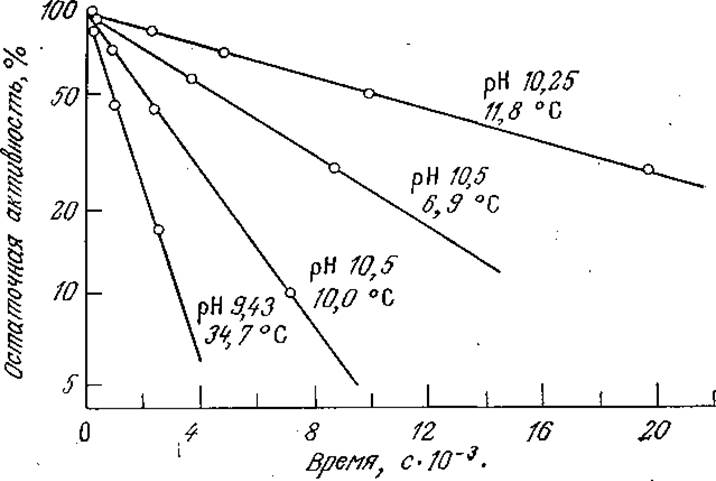
РИС. 3.27. Зависимость инактивации аденозинтрифосфатазы от времени при различных pH и температуре. [Воспроизведено с разрешения из статьи: Pelletier G. Е., Quellet L., Influence of Temperature and pH on Myosin Inactivation; Can. J. Chem., 39, 265 (1961).]
Данные об инактивации ферментов обычно получают, выдерживая фермент некоторое время в вызывающих денатурацию условиях без субстрата, после чего действие денатурирующих факторов снимают, создают некоторые стандартные условия, добавляют субстрат и определяют активность по начальной скорости ферментативной реакции. В присутствии субстрата скорость инактивации фермента может существенно отличаться от скорости, определенной описанным выше путем, если, например, свободный фермент и фермент-субстратный комплекс (или комплекс фермента с продуктом реакции) инактивируются с различными скоростями или если субстрат и (или) продукт реакции сами инициируют инактивацию фермента. Одну из возможностей анализа таких систем мы покажем на простом примере. Допустим, что связывание субстрата с ферментом стабилизирует последний (подобный эффект в известной степени действительно наблюдался в ряде систем). Таким образом, в нашем примере инактивации будет подвергаться только свободный фермент.
Таблица 3.10. Энергия активации и энтропия денатурации ферментовa
Фермент |
pH |
Энергия активации, ккал/моль |
Энтропия активации ∆S*, э. ед./моль |
Панкреатическая липаза |
6,0 |
46,0 |
68,2 |
Трипсин |
6,5 |
40,8 |
44,7 |
Пепсин |
4,83 |
56—147 |
Нет данных |
Аденозщітрифосфатаза |
7,0 |
70 |
150,0 |
8 Воспроизведено из работы: Laidler К. I., Bunting Р. S., The Chemical Kinetics of Enzyme Action, 2d ed., p. 430, Oxford University Press, London, 1973.
Комбинируя такую модельную систему инактивации с простой последовательностью элементарных реакций Михаэлиса и Ментен [уравнение (3.4)], получим
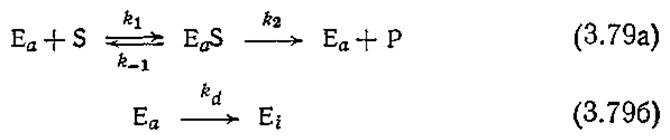
Если мы далее достаточно обоснованно допустим, что процесс инактивации происходит значительно медленнее, чем реакции (3.79а), то, привлекая приближение квазистационарного состояния для комплекса (EaS), получим следующее выражение для скорости реакции:
![]()
где etot,a — общая концентрация активного фермента как в свободной форме, так и в виде комплекса. Скорость изменения etot,a выражается уравнением
![]()
Возвращаясь к расчетам кинетики квазистационарного состояния, применявшимся при выводе уравнения (3.80), мы можем выразить еа через etot,a и параметры каталитической реакции; тогда уравнение (3.81) приобретет такую форму:
![]()
Из уравнений (3.80) и (3.82) следует, что скорости превращения субстрата и инактивации фермента взаимосвязаны. В частности, скорость инактивации фермента зависит от концентрации субстрата. С другой стороны, если Еа и (EaS) инактивируются с одинаковыми скоростями, то в условиях ферментативной реакции активность фермента будет снижаться точно так же, как и в отсутствие субстрата.
Обобщая эти рассуждения, нетрудно прийти к выводу, что вследствие различия в скоростях инактивации разных форм фермента (свободного фермента, разнообразных комплексов, ионизированных состояний и т. д.) скорость общей реакции зависит от любого параметра (концентраций субстрата и ингибитора, pH и т. д.), влияющего на относительные количества разных форм фермента. В частности, для описания сложной зависимости скорости инактивации от pH была разработана следующая модель:
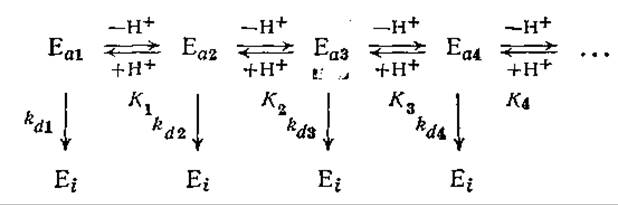
На рис. 3.28 в качестве примера такого сложного процесса изображена зависимость скорости инактивации рицина от pH (рицин не является ферментом; содержание активной формы белка определяли путем измерения растворимой фракции белка). Для некоторых других белков также наблюдался минимум скорости инактивации при определенном значении pH.
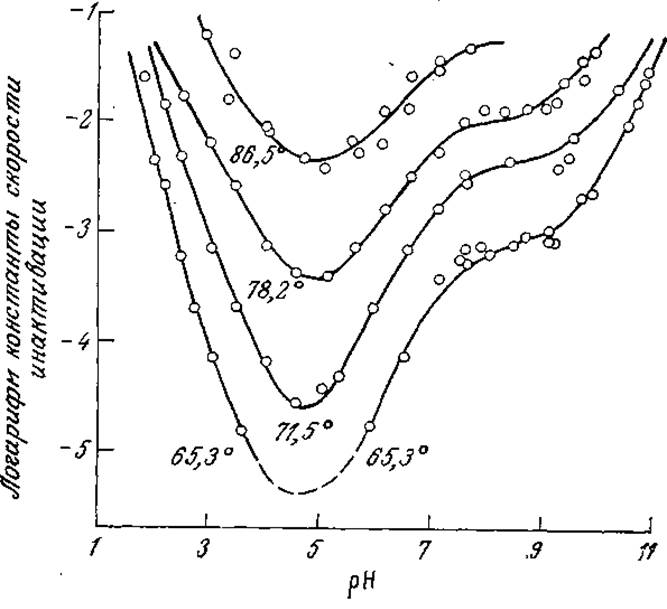
РИС. 3.28. Зависимость константы скорости реакции первого порядка инактивации рицина от температуры и pH. [Воспроизведено с разрешения из статьи: Levy М., Benaglia А. Е., The Influence of Temperature and pH upon the Rate of Denaturation of Ricin, J. Biol. Chem., 186, 829 (1950).]
Снижение ферментативной активности во времени не всегда соответствует реакции первого порядка, т. е. уравнению (3.78). Для ряда белков найдены нелинейные зависимости логарифма активности от времени, иногда на соответствующих кривых имеется по два различных прямых участка (рис. 3.29, а). Для объяснения и анализа таких систем предложен ряд моделей. Одна из них, включающая параллельные обратимую и необратимую инактивации, нашла применение при объяснении и анализе снижения активности некоторых ферментов:
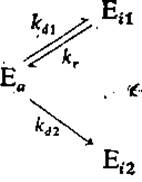
В частности, эта модель, предполагающая кинетику первого порядка для каждой из указанных элементарных реакций, успешно использовалась для интерпретации результатов изучения инактивации люциферазы, приведенных на рис. 3.29, а. Кривая процесса инактивации при 45 °С, например, была получена расчетным методом с помощью параметров kd1 = kd2 = 1,02 и kr = 0,02 ч-1.
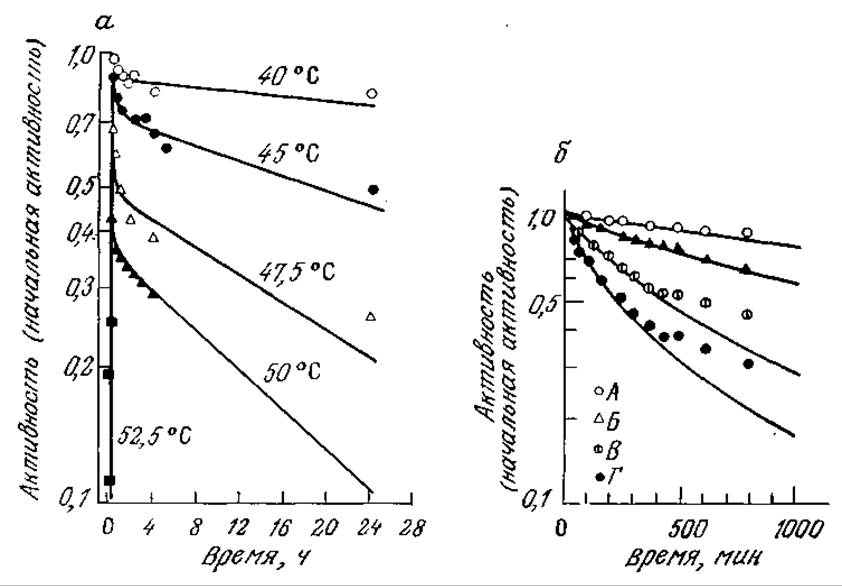
РИС. 3.29. а — инактивация препарата люциферазы при pH 6,8 и указанной температуре. [Воспроизведено с разрешения из статьи: Chase А. М., Studies on Cell Enzyme Systems. IV. The Kinetics of Heat Inactivation of Cypridina Luciferase, J. Gen. Physiol., 33, 535 (1950).] б — инактивация а-химотрипсина в растворе при pH 7,8, температуре 40 °С, концентрации Са2 + 10-3 М и начальной концентрации фермента 7,3∙10-7 М (A), 3,65∙10-6 М (Б), 1,46∙10-5М (В) и 2,92∙10-5 М (Г). [Воспроизведено с разрешения из статьи: Kawamuга Y., Nakanishi К., Matsuno R., Kamikubo Т., Stability of Immobilized a-Chymotrypsin, Biotech. Bioeng., 23, 1219 (1981).]
Потеря активности в растворах протеаз представляет собой более сложный процесс, поскольку протеазы катализируют реакцию собственного гидролиза. Эта особенность (автолиз) должна учитываться и в соответствующей модели инактивации. Приведенная ниже модель инактивации протеазы а-химотрипсина является вариантом модели (3.83), дополненной стадией автолиза:
![]()
![]() неактивные продукты гидролиза (пептиды) (3.84)
неактивные продукты гидролиза (пептиды) (3.84)
Некоторые особенности этой последовательности реакций были подтверждены химическими методами. Обратите внимание, в частности, на то, что только обратимо инактивированная форма Ei, этого очень хорошо изученного фермента способна подвергаться атаке и гидролизу активной формой протеазы Ea. Более глубокий анализ этой модели и ее применение для расчета кривых, изображенных на рис. 3.29,6, предлагается в упражнении 3.14.
Завершая обзор кинетики инактивации ферментов, следует упомянуть о подходах к анализу необратимых реакций инактивации ферментов ядами. В простейшем случае имеем
Еa + яд → Ed rd = kd∙ea∙(яд) (3.85)
Поскольку, однако, яды часто действуют на активный центр фермента, доступ к которому может быть блокирован связанным с ферментом субстратом, то в присутствии последнего ход анализа следует опять-таки видоизменить. Очевидно, нам нужно рассматривать процессы катализа, например реакцию (3.79а), и отравления фермента (3.85) совместно, причем в последнем уравнении Еа будет обозначать свободный, не связанный в комплекс фермент. Подобные видоизмененные модели, которые мы не будем здесь рассматривать, могут быть созданы и для процессов инактивации, описываемых уравнениями (3.83) и (3.84).