Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Кинетика катализируемых ферментами реакций
Ферментативные реакции в гетерогенных системах
До сих пор основное внимание мы уделяли поведению ферментов в растворе, где и осуществляется их взаимодействие с растворенными субстратами. Однако, как мы уже указывали, такая ситуация не является единственно возможной. Так, на рис. 2.27, где схематически изображена прокариотическая клетка, было показано, что некоторые клеточные ферменты связаны с мембранами клетки. Аналогичные структуры имеются и в эукариотах; в митохондриях, например, со сложной системой внутренних мембран связаны ферменты, отвечающие за очень сложную последовательность реакций.
Как показано на рис. 3.31, в природе и в биохимической технологии возможны многие другие сочетания различных физических состояний фермента и субстрата. Здесь мы рассмотрим кинетику ферментативных реакций между растворами ферментов и нерастворимыми субстратами, а в следующей главе изучим реакции растворимых субстратов, катализируемые связанными с носителями ферментами.
Если субстрат одновременно может существовать в нескольких фазах, то иногда ферментативной реакции подвергается только та его часть, которая находится в растворе. Примером могут служить данные, приведенные на рис. 3.32. Поскольку все вещества в той или иной степени растворимы в воде, то небольшое количество субстрата всегда будет находиться в растворе и, следовательно, подвергаться действию фермента. В то же время скорость этого процесса может быть настолько мала, что с практической точки зрения он не будет представлять никакого интереса. Теперь рассмотрим некоторые примеры другого рода.
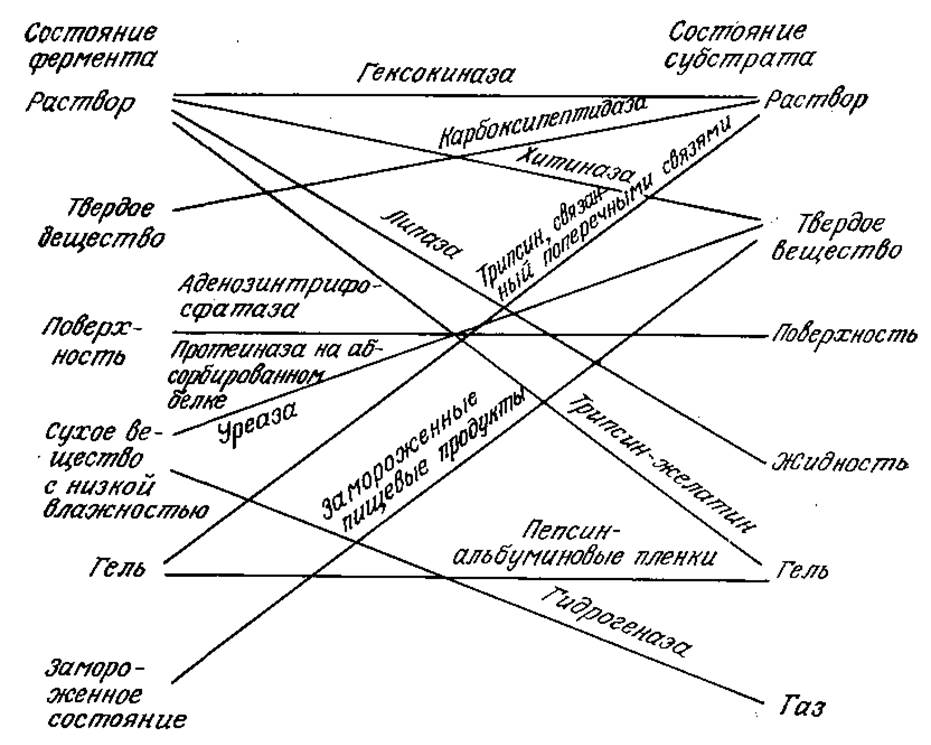
РИС. 3.31. Находящиеся в различных физических состояниях ферменты катализируют превращения различных форм субстратов. Классический случай ферментативной реакции в растворе является только одним из множества возможных вариантов фермент-субстратных взаимодействий. [Воспроизведено из статьи: McLaren A. D., Packer L., Some Aspects of Enzyme Reactions in Heterogeneous Systems, Adv. Enzymol. Rel. Sub. Biochem., 33, 245 (1970).]
Одним из таких примеров может являться реакция гидролиза метилбутирата под действием панкреатической липазы — фермента, образующегося в пищеварительном тракте человека и способного расщеплять жиры. В отличие от предыдущего примера здесь реакция не идет до тех пор, пока в реакционной смеси не сформируется нерастворимая форма субстрата в виде небольших капель (рис. 3.33). Очевидно, этот фермент способен проявлять свою активность только на границе раздела двух жидких фаз. Учитывая возможность денатурации фермента за счет поверхностного натяжения, интересно отметить, что, как и в случае упоминавшегося выше метода пенного фракционирования в присутствии детергентов, поверхностное натяжение на жировых каплях может существенно снизиться вследствие адсорбции желчных кислот — природных поверхностно-активных веществ, выделяемых в пищеварительный тракт.
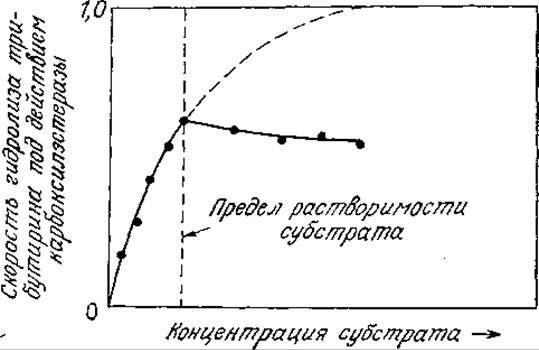
РИС. 3.32. Ферментативная реакция осуществляется только с растворенной формой субстрата. (Из работы: Диксон М., Уэбб Э., Ферменты, т. 1—3, — М.: Мир, 1982, т. 1, с. 122.]
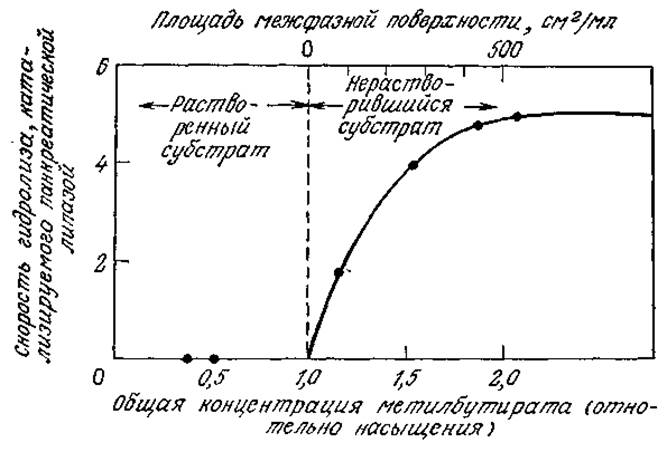
РИС. 3.33. Реакция на поверхности раздела двух жидких фаз. [Воспроизведено с разрешения из статьи: Sarda L., Desnuelle Р., Action de la Lipase Pancreatique sur les Esters en Emulsion, Biochim. Biophys. Acta, 30, 513 (1958).]
Другие ферменты активны в отношении как растворимой, так и нерастворимой форм субстрата. Так, например, было показано, что протеолитический фермент трипсин способен расщеплять как свободный лизоцим, так и лизоцим, адсорбированный на поверхности каолинита. Сам лизоцим также может взаимодействовать с растворимыми и «нерастворимыми» субстратами. Как мы уже отмечали, лизоцим активно разрушает стенки бактериальных клеток; в то же время он способен катализировать и расщепление растворимых олигомеров, образующихся из полимеров клеточной стенки (разд. 3.4.2).
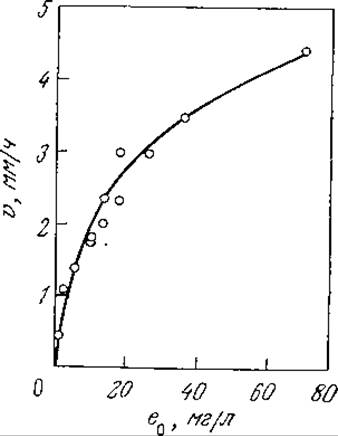
РИС. 3.34. Зависимость скорости разрушения твердого субстрата (тиогеля) от концентрации во фермента в растворе. [Данные из статьи: Tsuk A. G., Oster G., Determination of Enzyme Activity by a Linear Measurement, Nature (London), 190, 721 (1961).]
Взаимодействие растворенного фермента с нерастворимым субстратом путем адсорбции на поверхности последнего может быть описано с помощью интересного варианта рассмотренных ранее кинетических уравнений. В отличие от предыдущих случаев, когда скорость реакции возрастала пропорционально общей концентрации фермента, здесь при повышении концентрации фермента скорость реакции сначала возрастает, а затем приближается к некоторой предельной величине. Такое поведение фермент-субстратной системы наглядно иллюстрируется приведенными на рис. 3.34 данными, отражающими кинетику гидролиза твердого блока белка (в данном случае тиогеля — сшитого поперечными связями желатина) под действием трипсина.
Разработку достаточно обоснованной модели для кинетики гетерогенной реакции мы начнем с допущения, обратного тому, которое было положено в основу анализа скоростей ферментативных реакций в растворе — теперь мы будем считать, что фермент адсорбируется на субстрате. Обозначив символом А вакантные центры на поверхности субстрата, мы можем написать следующее уравнение:
![]()
Если общее число молей центров адсорбции на поверхности субстрата в расчете на единицу объема реакционной смеси принять равным a0, то
а0 = а + (еа) (3.87)
Из уравнения (3.87) и уравнения равновесной адсорбции фермента (3.86) следует, что
![]()
Теперь остается только допустить, что реакция завершается необратимым расщеплением комплекса ЕА. Следовательно,
![]()
По условиям модели е обозначает концентрацию свободного фермента, которая в начале эксперимента связана с общей концентрацией фермента е0 соотношением
е0 = е + (еа) (3.90)
Если начальная концентрация фермента значительно превышает начальную концентрацию субстрата (е0 ≫ а0), то с хорошей степенью приближения можно считать, что
е0 ≈ е (3.91)
Поэтому
![]()
Для реакций с твердыми субстратами ситуации, когда е ≫ а0, ни в коей мере не являются исключением. Например, результаты, приведенные на рис. 3.34, были получены в эксперименте, в котором отношение е0/а0 составляло около 4000. Этим гетерогенные реакции резко отличаются от реакций в растворах, когда s0 обычно значительно больше, чем е0.
Из уравнения (3.92) следует, что график зависимости 1/v от 1/е0 (в двойных обратных координатах Лайнуивера — Бэрка) должен представлять собой прямую линию. Как показано на рис. 3.35, так оно и есть на самом деле. Здесь прямая на рис. 3.35, а выражает в другой форме те же данные, которые были приведены на рис. 3.34, а на рис. 3.35,6 отражены аналогичные результаты, полученные для другой системы растворимый фермент — нерастворимый субстрат.
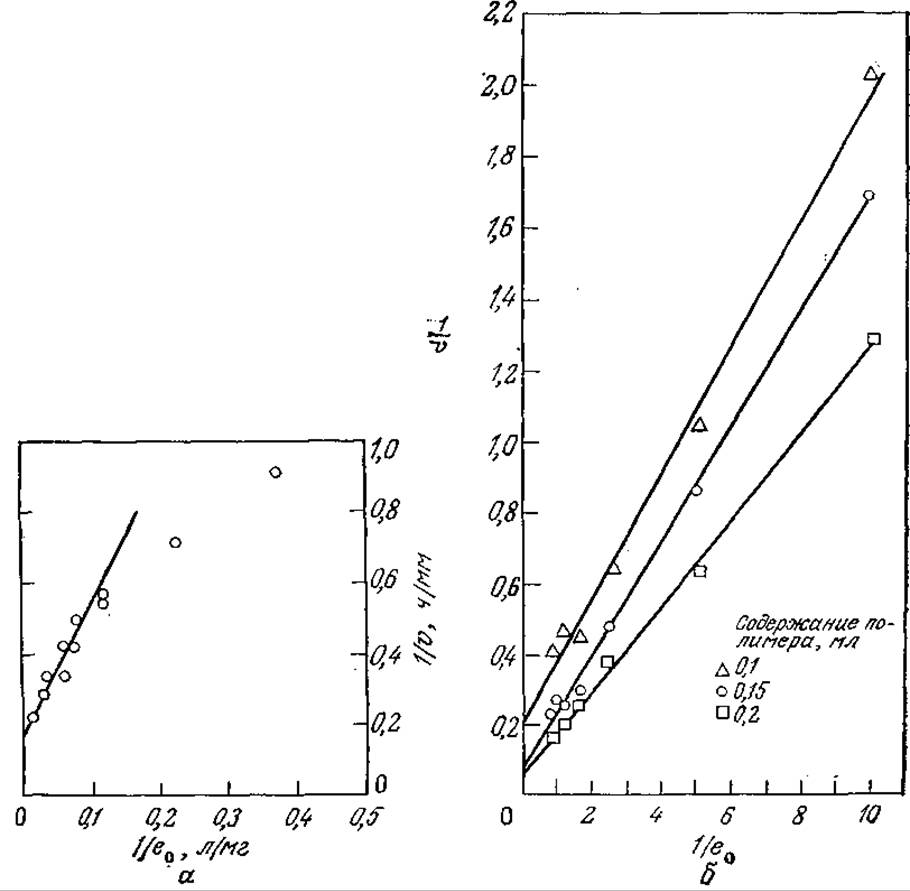
РИС. 3.35. а — зависимость скорости деструкции твердого субстрата (тиогеля) (1/v) от концентрации трипсина (1/e0) в растворе в координатах Лайнуивера—Бэрка. б — зависимость скорости деструкции нерастворимого субстрата (частиц поли-β-гидроксибутирата) раствором фермента (деполимеразы из Р. temoignei). [Воспроизведено из работы: McLaren A. D., Packer L., Some Aspects of Enzyme Reactions in Heterogeneous Systems; Adv. Enzymol. Rel. Sub. Biochem, 33, 245 (1970).]
Многие источники питательных веществ для микроорганизмов представляют собой твердые частицы (в потоках сточных вод, озерах, хранилищах компоста и т. д.). Очевидно, что адсорбции и транспорту растворенных питательных веществ через клеточные мембраны должен предшествовать гидролиз этих частиц внеклеточными ферментами. Точно так же гидролиз целлюлозы ферментами типа целлюлаз требует предварительного расщепления нерастворимых частиц, поэтому надо полагать, что рассмотренная в этом разделе кинетика гетерогенных ферментативных реакций окажется пригодной для расчетов реакторов с такого типа субстратами.
В заключение следует подчеркнуть, что область применения рассмотренной кинетической модели не ограничивается твердыми субстратами; она использовалась и для описания нерастворимых жидких субстратов, диспергированных в растворе фермента (например, системы, кинетика которой изображена на рис. 3.33). Кроме того, здесь мы не принимали во внимание различий в концентрациях реагентов в основной массе жидкой фазы и на границе раздела фаз. Последнюю проблему мы рассмотрим детально в следующей главе.
Упражнения
3.1. Определение Кm и Vmax. В табл.3У1.1 приведены начальные скорости катализируемой ферментом реакции при различных концентрациях субстрата.
а) Определите vmax и Кm методом Лайнуивера — Бэрка.
б) Определите те же величины графически в координатах Эдн—Хофсти.
в) Вычислите стандартные отклонения наклонов прямых и отсекаемых на координатных осях отрезков для каждого метода.
Таблица 3У1.1
S, моль/л |
v, моль/(л∙мин)∙106 |
S, моль/л |
v, моль/(л∙мин) ∙ 10а |
4,1∙10-3 |
177 |
4,9∙10-5 |
80 |
9,5∙10-4 |
173 |
1,06∙10-5 |
67 |
5,2∙10-4 |
125 |
5,1∙10-6 |
43 |
1,03∙10-4 |
106 |
3.2. Ферментативная реакция в реакторе периодического действия. Фермент с Km= 1 ∙ 10-3 М инкубировали с субстратом при начальной концентрации последнего 3∙10-5 М. Через 2 мин прореагировало 5% субстрата. Какое количество субстрата будет трансформировано в течение 10, 30 и 60 мин?
3.3. Кинетика ферментативных реакций при участии ферментов с несколькими активными центрами. Предположим, что фермент обладает двумя активными центрами, так что субстрат трансформируется в продукт реакции в соответствии со следующей последовательностью элементарных реакций:
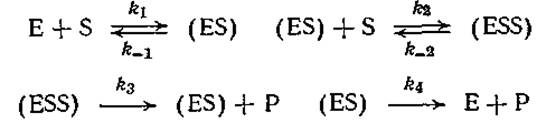
Приняв условия квазистационарного состояния для (ES) и (ESS), найдите выражение, определяющее скорость образования Р.
3.4. Образование нескольких фермент-субстратных комплексов. В ходе катализируемых ферментами реакций иногда промежуточно образуется несколько комплексов. Найдите соответствующие выражения для скорости реакции, применив а) равновесный подход Михаэлиса и б) приближение квазистационарного состояния для комплексов, если имеет место следующая последовательность реакций:
![]()
3.5. Релаксационная кинетика с синусоидальными возмущениями. Как показано на рис. 3У5.1, если параметры реагирующей системы, находящейся в равновесии (или в стационарном состоянии), подвергаются небольшому возмущению по синусоидальному закону, то и концентрации реагирующих веществ также изменяются по такому же закону.
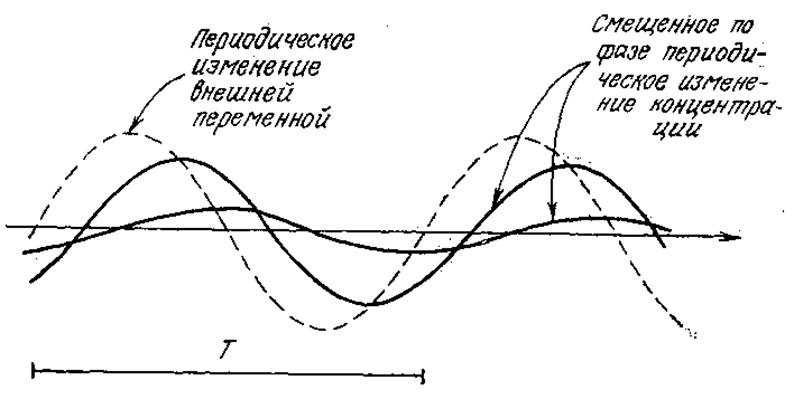
РИС. 3У5.1.
Найдите уравнения, связывающие наблюдаемые флуктуации концентраций с кинетическими параметрами, для реакции
![]()
если средняя температура изменяется в соответствии с уравнением
Т = Т0(1 + asin ωt), где а ≪ 1
Покажите, как вы будете определять k1 и k2, если известны отклики а и b на периодические возмущения.
3.6. Обратимые реакции. Предположим, что мы изучаем обратимую реакцию:
![]()
а) Покажите, что равновесие будет значительно смещено вправо только при условии k1k2 ≫ k-1k-2.
б) Покажите, что параметры vs, vp, Ksи Кp не являются независимыми.
в) При каких условиях графическое решение уравнения задачи (б) в координатах Лайнуивера — Бэрка даст полезные результаты?
г) Путем интегрирования dp/dt для приведенной последовательности реакций определите зависимость р от t и значения р при равновесии
![]()
д) Покажите, что В = 0, если Ks = Kp.
3.7. Инактивация ферментов. Пусть фермент необратимо инактивируется в соответствии с уравнением (3.77).
а) Покажите, что в таком процессе изменяется только vmax, но не Кm.
б) Покажите, что для ферментов, действующих на нерастворимые субстраты [уравнение (3.92)], можно ошибочно найти решение, противоположное решению задачи (а), если не принять во внимание изменение концентрации активной формы фермента.
3.8. Зависимость от pH. В результате катализируемой ферментом необратимой реакции генерируются протоны в соответствии со следующим уравнением:
H2O + E + S+ → E + SOH + H+
Допустим, что е- — концентрация активной формы фермента и что e-/e = 1,0 при рН = 6,0 = рK1, е2-/е- = 1,0 при рН = 10,0 = рK2.
а) Покажите, что скорость реакции при pH 7,0 приближенно выражается уравнением
![]()
б) Путем интегрирования предыдущего уравнения покажите, что изменение s во времени осуществляется по закону
![]()
где а и ß — параметры, зависящие от начальных pH и концентрации субстрата.
3.9. Кинетика ингибирования. Пестицид ингибирует активность данного фермента А, и, следовательно, последний может применяться для определения пестицида в пробах неизвестного состава.
а) В лабораторных экспериментах измерены начальные скорости реакции; результаты измерений приведены в табл. 3У9.1. Каким ингибитором является этот пестицид, конкурентным или неконкурентным? Определите величины Ki, vmax и Кm.
Таблица 3У9.1
v, моль/(л∙мин) ∙ 106 |
||
s, моль/л |
В отсутствие ингибитора |
В 10-5 М растворе ингибитора |
3,3∙104 |
56 |
37 |
5,0∙10-4 |
71 |
47 |
6,7∙104 |
88 |
61 |
1,65∙10-3 |
129 |
103 |
2,21∙10-3 |
149 |
125 |
б) Раствор фермента (50 мл), описанного в задаче (а), смешали с 50 мл 8∙10-4 М раствора субстрата и 25 мл пробы; начальная скорость реакции составила 18 мкмоль/(мин∙л). Какова концентрация ингибитора в пробе, если последняя не содержит других ингибиторов (кроме пестицида) и субстратов?
3.10. Кинетика ферментативных реакций, протекающих с участием ионизирующегося кофактора. Для проявления каталитической активности ферменту необходим связанный кофактор. Связь кофактора с ферментом очень прочная. Необходимая для проявления активности группа кофактора имеет рК, равное рКс; кофактор активирует фермент только в депротонированной форме. Первые значения рК активного центра фермента по обе стороны от pH максимальной активности фермента равны pK1и рK2. Найдите (или просто напишите) соответствующие выражения для скорости превращения индивидуального субстрата в продукт реакции при следующих условиях:
а) |рКс| ≪ |pK1| ≪ |рK2|
б) |pK| ≪ |pKc| ≪ |рК2|
в) рКс = рК1
3.11. Субстратная активация. Найдите уравнения, описывающие скорость ферментативной реакции при активации субстратом:
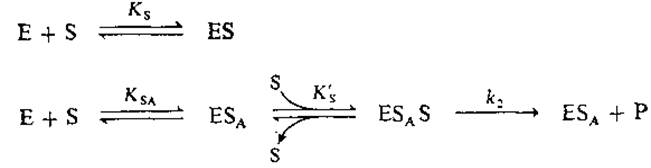
Как обычно, примите, что а) промежуточные соединения находятся в квази-стационарном состоянии и б) концентрация субстрата значительно превышает концентрацию фермента.
3.12. Выделение тепла в процессе ферментативных реакций. Максимальное повышение температуры в реакторе полного вытеснения можно определить с помощью уравнения теплового баланса превращения субстрата при его однократном прохождении через реактор.
а) Учитывая, что количество выделившейся теплоты больше количества теплоты, переданной жидкой среде (или равно ему), выразите максимальное повышение температуры в катализируемой одним ферментом реакции через теплоту реакции на моль реагента ∆Нr, относительное количество прореагировавшего реагента δ, концентрацию реагента на входе в реактор s0, теплоемкость жидкости Ср и ∆Т = Твыход—Твход.
б) Покажите, что для гидролиза 20%-ного раствора лактозы на 80% [∆Нr = -7100 кал/(г∙моль)] максимальное повышение температуры составляет всего лишь несколько градусов.
в) Если тонкостенный ферментный реактор снабжен охлаждающей рубашкой, то температуру в средней линии выхода приближенно можно определять по уравнению
![]()
где z — длина колонны, t — время пребывания реакционной массы в реакторе и a = kt/pCp, где kt— общая теплопроводность, р — плотность слоя насадки и erf — функция погрешности (таблицы значений этой функции для различных аргументов можно найти в любом справочнике). Покажите, что для условий, описанных в части (б) настоящего упражнения, Т* быстро приближается к единице (вычислите Т* при 2 = 1, 2, 3, 4 дюйма). (Pitcher W. Н., Immobilized Enzymes for Industrial Reactors, p. 151, Academic Press, New York, 1975.)
3.13. Уравнение Хилла для кооперативного связывания. Для описания кооперативного (n > 1) связывания субстратов (S) с олигомерными белками (Еn) часто применяется следующая простая модель:
![]()
Найдите простой графический метод определения n, если известен ряд экспериментально определенных значений EnSn.
3.14. Инактивация а-химотрипсина. Рассмотрим процессы тепловой денатурации и автолиза а-химотрипсина, одновременно протекающие в соответствии с уравнением (3.84), где К — константа равновесия реакции между Еа и Еi1, a Km— константа диссоциации комплекса ЕаЕi1. Принимая, что (еаeі1) ≪ e0 + ei1, определите зависимость концентрации потенциально активного фермента е (е = еа + еі1) от времени в реакторе периодического действия.
Литература
Во всех перечисленных в конце гл. 1 руководствах по биохимии дается и введение в кинетику ферментативного катализа. Особенно подробно и на современном уровне эта проблема освещена в книге Малера и Кордеса (ссылка [4] в гл. 2). Более подробную информацию читатель может найти в следующих книгах и статьях.
1. Bernhard A., Structure and Function of Enzymes, W. A. Benjamin, New York, 1968. Короткое, написанное очень доступным языком введение в энзимологию.
2. Диксон М., Уэбб Э., Ферменты, т. 1—3. — М.: Мир, 1982. Самое полное однотомное руководство по химии и биологии ферментов, являющееся настольной книгой для любого энзимолога. В нем имеется обширная глава (200 страниц), посвященная кинетике ферментативного катализа. Кроме того, в монографии рассмотрены многие другие проблемы энзимологии, приведена большая таблица ферментов и катализируемых ими реакций, дана обширная библиография.
3. Laidler К. J., Bunting Р. S., The Chemical Kinetics of Enzyme Action, 2d ed., Oxford University Press, London, 1973. В этой монографии более подробно рассмотрена кинетика ферментативного катализа и представлен обширный экспериментальный материал, подтверждающий различные математические выражения, предложенные для определения скоростей реакций.
4. Schmid R. D., Stabilized Soluble Enzymes, in Advances in Biochemical Engineering, Vol. 12: Immobilized Enzymes II, p. 41, Ghose T. K., Fiechter A., Blakebrough N. (eds.), Springer-Verlag, Berlin, 1979. Превосходная обзорная статья, в которой дан глубокий анализ причин и факторов, вызывающих денатурацию белков, а также великолепный обзор методов повышения стабильности ферментов.
5. Johnson F. Н., Eyring Н., Polissar М. J., The Kinetic Basis of Molecular Biology, John Wiley and Sons, Inc., New York, 1954. Великолепная монография, в которую включено множество данных о влиянии температуры, pH, давления и ингибиторов на ферментативную и другие виды биологической активности, а также интерпретации этих данных. Особое внимание уделено применению термодинамики и теории абсолютных скоростей реакций.
6. Жоли М., Физическая химия денатурации белков. — М.: Мир, 1968. Хотя в эту монографию, естественно, не включены многие последние данные, в ней рассмотрены все основные явления, связанные с причинами, проявлениями, обнаружением и изучением денатурации белков. Все эти явления рассматриваются с точки зрения химика.
7. McLaren A. D., Packer L., Some Aspects of Enzyme Reactions in Heterogeneous Systems, Advan. Enzymol., 33, 245 (1970). Превосходная обзорная статья, в которой рассмотрено множество гетерогенных ферментативных реакций, протекающих в биологических системах в природных условиях. Эта работа посвящена важной, но относительно мало изученной теме поведения нерастворимых субстратов, а также связанных ферментов в клетке и почве.