Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Применение реакций, катализируемых ферментами
Заключение
Мы познакомились с основными направлениями промышленного применения ферментных катализаторов, узнали, как ферменты можно иммобилизовать для использования в непрерывных процессах, и изучили особенности кинетики реакций, катализируемых иммобилизованными ферментами. Теперь обратимся к рассмотрению природных многоферментных систем, характерных для живых клеток, в которых осуществляются сложнейшие разветвленные последовательности катализируемых ферментами реакций, часто обладающие элементами обратной связи.
Следующая глава посвящена стехиометрии и термодинамике взаимосвязанных клеточных реакций. Затем в гл. 6 будут рассмотрены системы регуляции и контроля этих последовательностей реакций, а в гл. 7 — кинетика роста популяций клеток. Прежде чем перейти к изучению биологических реакторов (гл. 9), в гл. 8 рассмотрим основные проблемы массопередачи и энергообмена. Если же читателя интересуют прежде всего реакторы для осуществления ферментативных процессов, то он может сразу ознакомиться с разд. гл. 9, в которых описываются основные проблемы анализа и проектирования биологических реакторов. В частности, разд. 9.1.2 и 9.1.4 посвящены исключительно анализу ферментативных реакторов, а несколько тем из разд. 9.6 по многофазным реакторам имеют непосредственное отношение к биологическим реакторам с иммобилизованными ферментами.
Упражнения
4.1. Нерастворимые субстраты. В результате смешения водной суспензии однородных по размерам частиц желатина (полиглицина) и порошкообразного протеолитического фермента получена смесь, содержащая а объемных частей желатина и е молей фермента в литре суспензии.
а) Приняв, что первоначальный размер частиц равен d0 и что единственным продуктом реакции является глицин, найдите выражения, описывающие зависимость скорости образования глицина и изменения размера частиц от времени. Примите также, что скорость реакции при s0≪e0 выражается уравнением Михаэлиса — Ментен, т. е.
![]()
где sa — площадь поверхности субстрата на единицу объема реакционной смеси.
б) Из проявленной фотопленки необходимо выделить серебро путем ферментативного гидролиза связывающего серебро желатина. Определите минимальное время контакта фотопленки с раствором фермента, за которое гидролизуется весь желатин.
4.2. Автокатализ. Можно принять, что в периодическом процессе кинетика автокаталитнческой активации пепсина (рис. 4.4) описывается уравнением Михаэлиса — Ментен.
а) Покажите, что максимальная скорость активации достигается при
![]()
б) Покажите, что ход реакции во времени описывается уравнением
![]()
в) Для указанной автокаталитнческой системы начертите график зависимости 1/v от 1/s в координатах Лайнуивера — Бэрка. График какой другой зависимости был бы более удобным?
4.3. Ферментативные реакции с несколькими субстратами. В промышленных ферментных реакторах в реакционной смеси часто присутствует несколько субстратов одновременно.
а) Покажите, что в системе с двумя субстратами скорость превращения S1 и S2 выражается уравнением
![]()
и что таким образом каждый субстрат является конкурентным ингибитором другого субстрата.
б) Найдите общее выражение, описывающее общую скорость реакции одного фермента с т субстратами одновременно.
4.4. Кинетика гидролиза целлюлозы. Гидролиз целлюлозы протекает с участием солюбилизирующего фермента, фермента, образующего дисахарид целлобиозу, и гидролизующей этот дисахарид ß-глюкозидазы (рис. 4,1). Первые два фермента ингибируются целлобиозой (будем считать, что целлобиоза представляет все олигомерные ингибиторы), поэтому упрощенная схема реакций будет выглядеть следующим образом:
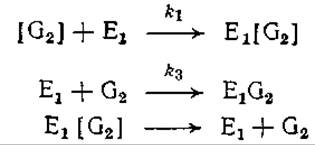
Здесь [G2] и G2 — нерастворимая целлюлоза и растворимая целлобиоза соответственно, а Е1 — фермент, катализирующий наиболее медленную стадию образования целлобиозы.
а) Можно допустить, что в отсутствие ß-глюкозидазы глюкоза не образуется. Найдите соответствующие выражения, исчерпывающе описывающие зависимость g2 от времени для случаев конкурентного и неконкурентного ингибирования.
б) Покажите, что по графику зависимости g2/t от (1/t)ln(s0/g2) можно различить системы без ингибирования, с конкурентным ингибированием и неконкурентным ингибированием. Почему в этом случае лучше применять g2, а не концентрацию непрореагировавшего субстрата? [Экспериментально показано, что описанная система ингибируется неконкурентно; см. статью: Howell J. A., Stuck J. D., Kinetics of Solka floe Hydrolysis by Trichoderma viride Cellulase; Biotech. Bioeng., 17, 873 (1975).]
4.5. Подбор биокатализатора для лимитируемого реакцией режима. Этиловый эфир ацетил-L-тирозина (АТЕЕ) гидролизуется иммобилизованным а-химотрипсином с удельной объемной скоростью 18,4 мкмоль АТЕЕ в 1 см3 за 1 с. Найдено, что эффективный коэффициент диффузии АТЕЕ равен примерно 3,8∙10-6 см2/с. Биокатализатор с каким радиусом сфер следует выбрать для изучения кинетических свойств иммобилизованного фермента в лимитируемом реакцией режиме?
4.6. Маскирование инактивации иммобилизованного фермента массопередачей. Рассмотрим иммобилизованный фермент, необратимо теряющий свою активность в соответствии с уравнением (3.78). Примем, что превращение субстрата является реакцией приблизительно первого порядка.
а) Предположим, что фермент иммобилизован на наружной поверхности непроницаемого для субстрата твердого носителя и что при t = 0 число Дамкелера велико. Начертите графики зависимости коэффициента эффективности и скорости реакции от времени. Какие ошибочные выводы относительно влияния иммобилизации на стабильность фермента можно сделать, если не ввести соответствующие поправки на эффекты массопередачи?
б) Ответьте на тот же вопрос в другой ситуации, когда фермент иммобилизован внутри проницаемой для субстрата пластины. Примите, что внешнее сопротивление массопередаче относительно невелико.
4.7. Гистерезис; влияние pH на иммобилизованный папаин. Изучение pH-электрода, на поверхность которого нанесен папаин, показывает, что зависимость генерируемого на поверхности электрода pH (внутреннего pH) от pH в растворе при различных направлениях изменения pH выражается разными кривыми. [В данном случае изучалась реакция гидролиза этилового эфира бензоиларгинина (ВАЕЕ) до соответствующей кислоты; см. рис. в статье: Naparstek A., Romette J. L., Kernevez J. Р., Thomas D., Nature, 249, 490 (1974).]
а) Приняв, что s0 ≫ Km, слой фермента очень тонок и активность папаина максимальна при pH 6,0, покажите, что это явление может быть обусловлено внешним сопротивлением массопередаче.
б) Кинетические константы этой реакции, катализируемой растворимым ферментом, при pH 6,0 и 20 °С равны: k2 = 19 международных единиц (1 международная единица равна количеству микромолей ВАЕЕ, гидролизуемых 1 мг фермента в 1 мин), K1 = 5∙10-3 М. Найдите величину коэффициента массопередачи иона водорода и соответствующее указанным константам значение рК2 фермента, если на поверхность электрода нанесено а мг/см2 фермента и активность иммобилизованного фермента составляет только 6% активности фермента в растворе. (Во всех случаях s ≫ Km.)
в) По найденной величине рK2 и приведенным в предыдущей части задачи параметрам вычислите коэффициенты эффективности при различных внешних pH; постройте график зависимости коэффициента эффективности от внешнего pH. Иногда коэффициент должен превышать единицу, а при некоторых pH задача должна иметь несколько решений. [См. также работу: Bailey J. Е., Chow М. Т. С., Biotech. Bioeng., 16, 1345 (1974).]
4.8. Стехиометрия реакций внутри частицы катализатора. Внутри пористой частицы иммобилизованного фермента осуществляется катализируемая ферментом реакция
![]()
где а, ß, у и δ — стехиометрические коэффициенты.
а) Используя уравнения материального баланса для субстратов и продуктов реакции, найдите выражения, определяющие концентрации всех веществ внутри частицы катализатора через концентрацию S1 (в той же точке частицы), концентрации на наружной поверхности частицы, а также эффективные коэффициенты диффузии субстратов и продуктов реакции.
б) Покажите, что реагент, ограниченно растворимый в реакционной среде, будет лимитировать скорости реакций внутри частицы иммобилизованного фермента.
4.9. Обратимая изомеризация глюкозы в насадочной колонне. Промышленно важный процесс изомеризации глюкозы во фруктозу осуществляют в реакторе колонного типа с неподвижным слоем иммобилизованной глюкозоизомеразы; кинетика катализируемой этим ферментом реакции описывается уравнением Михаэлиса — Ментен для обратимых реакций [уравнение (3.18)].
а) Покажите, что подстановка в указанное уравнение s = s - se (se — равновесная концентрация) приводит к простому уравнению Михаэлиса — Ментен (относительно s). Как в этом уравнении будут выражены кажущиеся константа Михаэлиса (Каpp) и максимальная скорость (vарр)?
б) Изменение s в зависимости от положения в одномерном неподвижном слое катализатора с пористостью ε и при средней скорости потока uz может быть описано уравнением
![]()
с одним краевым условием: s = s0 - se при z = 0. Путем интегрирования этого выражения найдите другое уравнение, определяющее параметры работы реактора через объемную производительность (т), определяемую как т = = L( 1—ε)/εuz [частное от деления объема реактора (катализатора) на объемную скорость потока].
в) Рассмотрим медленно инактивирующийся иммобилизованный фермент, находящийся в реакторе с неподвижным слоем катализатора, описанным в части «б» настоящей задачи. Если процесс инактивации подчиняется закону е(активн.) = e(t = 0)exp( - kdt), найдите по измененным соответствующим образом данным предыдущей задачи функцию f[s0, vm,app > s(L)], график зависимости которой от времени t позволил бы определить как τ, так и kd.
4.10. Иммобилизованный ферментный катализатор с неравномерным распределением фермента. Приняв, что катализируемая реакция имеет первый порядок, сравните общие скорости и коэффициенты эффективности, когда иммобилизованный в пористой пластине фермент, имеющий одно и то же число единиц ферментативной активности
а) распределен равномерно по всему объему пластины;
б) сконцентрирован и равномерно распределен во внешнем слое пластины вблизи наружной поверхности катализатора, причем во внутренней области, толщина которой равна половине толщины пластины, фермент совершенно отсутствует.
4.11. Одновременная оценка параметров кинетики реакции и массопередачи. Фермент иммобилизован на поверхности непористого твердого тела. Приняв, что внешним сопротивлением массопередаче нельзя пренебречь и что собственная кинетика ферментативной реакции описывается уравнением Михаэлиса — Ментен:
а) найдите выражение, четко определяющее коэффициенты в координатах Лайнуивера — Бэрка; с помощью этого уравнения выразите кажущиеся максимальную скорость (vmaxapp) и константу Мнхаэлиса (Kmарр) через реальные переменные vmax. Kmи ks(коэффициент массопередачи);
б) покажите, как можно графическим путем определить параметры vmах, Кm и ks, если имеются данные для достаточно большого диапазона концентраций субстратов.
4.12. Кинетика реакций иммобилизованных ферментов с разделением зарядов. Концентрацию заряженного вещества (субстрата, ингибитора) на заряженной матрице, например на ферментной мембране, можно выразить следующим уравнением:
![]()
где z — ионный заряд субстрата или ингибитора; е — заряд электрона; ψ — электростатический потенциал мембраны (ψ (раствор) = 0). Покажите, что кажущиеся величины Ks и K1 определяются выражением
![]()
если рассматривать концентрации в объеме всего раствора. Допуская, что в мембране имеются е, е-, е2- (е- — активная форма фермента), покажите, что максимальная начальная скорость реакции (если пренебречь влиянием массопередачи) достигается в случае матрицы-носителя фермента с ψ, определяемым уравнением
![]()
где а = еzеψ/RТ и h0 = [Н+] в основной массе раствора.
4.13. Микрокапсулирование; ß-галактозидаза. Гидролиз лактозы ß-галактозидазой ингибируется продуктом реакции, и поэтому уравнение, выражающее скорость этой реакции, имеет форму
![]()
С целью облегчения процесса выделения ß-галактозидазы из молока раствор фермента заключен в микрокапсулы из нитроцеллюлозы диаметром около 30 мкм.
а) Постройте график в координатах Лайнуивера — Бэрка для р = 0; 0,5; 1,5; 5 и 10 мМ (е0 = 75 мг в 100 мл) при условии, что vm = kpe0, kp = 0,57 мкмоль/(мг фермента в минуту), Km = 0,54 мМ, Ki = 1,5 мМ.
б) На основе графика части «а» задачи, не привлекая приведенное в условии уравнение, постройте графики зависимости 1/v от 1/s для периодического процесса при следующих начальных условиях:
Sq, мМ |
0,5 |
5,0 |
10,0 |
5,0 |
р0, мМ |
0 |
0 |
0 |
5,0 |
в) Покажите, что даже при максимально возможной скорости реакции в микрокапсуле в системе, описанной в части «а», скорость процесса лимитируется реакцией, т. е. диффузия субстрата и продукта реакции осуществляются быстрее, чем сама реакция [см. статью: Wadiak D. Т., Carbonell R. G., Kinetic Behavior of Microencapsulated ß-Galactosidase, Biotech. Bioeng., 17, 1157 (1975)1.
4.14. Мембранный биореактор. Фермент удерживается в проточном биореакторе полупроницаемой мембраной. Активный фермент инактивируется в ходе реакции первого порядка с константой скорости kd. Постоянство состава продуктов реакции обеспечивают путем постепенного введения активного фермента в реактор, чтобы концентрация активного фермента в нем была постоянной, равной еа. На мембране концентрируется гелеобразный слой фермента, увеличивающий сопротивление потоку раствора, поэтому с целью обеспечения постоянной скорости потока J реакционной смеси через мембрану приходится непрерывно регулировать падение давления на мембране. В то же время необходимая скорость потока J может быть достигнута только в том случае, если общая концентрация фермента etot (сумма активной и неактивной форм) не превышает некоторое максимально допустимое значение, определяемое уравнением
emax = es exp (—J/ke)
где es — концентрация насыщения фермента и ke — коэффициент массопередачи фермента.
а) Определите зависимость общей концентрации фермента в реакторе от времени.
б) Если скорость потока падает ниже J, то процесс следует остановить, а реактор подвергнуть чистке. Определите максимальное время непрерывной работы реактора tmах как функцию J.
в) Найдите значение J, позволяющее получить максимальное количество продукта реакции за период непрерывной работы реактора (0 ≤ t ≤ tmax) при е0 = 5 кг/м3, es = 100 кг/м3, kе = 0,017 мм/с, kd = 0,018 сут-1.
г) Решите задачу «в» при е0 = 50 кг/м3 (все другие параметры не изменяются).
д) Как влияет константа скорости инактивации kd на величину J, определяемую по условиям задачи «в»? На какие другие важные с экономической точки зрения параметры влияет kd?
Литература
В большинстве работ, приведенных в конце гл. 3, содержится материал, относящийся и к темам настоящей главы. Кроме того, многие проблемы технологии ферментов рассмотрены и в ряде других литературных источников, к числу которых относятся:
1. Tauber H., The Chemistry and Technology of Enzymes, John Wiley and Sons, Inc., New York, 1949.
2. Underkofler L. A., Manufacture and Use of Industrial Microbial Enzymes, Bioeng. Food Process. CEP Symp. Ser. no. 69, 62, 11 (1966).
3. Faith W. TNeubeck С. E., Reese E. T., Production and Application of Enzymes, Advan. Biochem. Eng., 1, 77 (1971).
4. Arima K., Microbial Enzyme Production, in Global Impacts of Applied Microbiology, Starr M. P. (ed.), John Wiley and Sons, Inc., New York, 1964.
5. Wolnak B. et al., The Present and Future Technological Status of Enzymes, U.S. Dept. Commerce Doc., PB-219636, Natl. Tech. Inf. Serv., December 1972.
6. Aunstrup K., Enzymes of Industrial Interest: Traditional Products, in Annual Reports on Fermentation Processes, Perlman D. (ed.), vol. 2, Academic Press, New York, 1978.
7. Godfrey T., Reichelt J., Industrial Enzymology, Macmillan Publishers Ltd., London, 1983.
В перечисленных ниже монографиях и сборниках содержится ценная информация о получении, идентификации и применении иммобилизованных ферментов:
8. Guilbault G. G.. Enzvmatic Methods of Analysis, Pergamon Press, New York, 1970.
9. Zaborsky O. R., Immobilized Enzymes, CRC Press, Cleveland, Ohio, 1973.
10. Insolubilized Enzymes, Salmona M., Saronio C., Garatlin S. (eds.), Raven Press, New York, 1974.
11. Olson A. C., Cooney C. L., Immobilized Enzymes in Food and Microbial Processes, Plenum Press, New York, 1974.
12. Immobilized Enzymes for Industrial Reactors, Messing R. A. (ed.), Academic Press, Inc., New York, 1975.
13. Immobilized Enzymes, Mosbach К. (ed.). Methods in Enzymology, vol. XLIV (Colwick S. P., Kaplan N. O., eds.-in-chief), Academic Press, New York, 1976.
14. Immobilized Enzymes, Research and Development, Chibata I. (ed.), Halsted Press, New York, 1978.
15. Characterization of Immobilized Biocatalysts, Buchholz K., (ed.), DECHEMA Monographs No. 1724—1731, vol. 31, Verlag-Chemie, Weinheim, 1979.
16. Chibata I., Tosa T., Sato T., Mori T., Matsuo Y., Preparation and Industrial Application of Immobilized Aminoacylases, in Fermetation Technology Today, Terui G. (ed.), p. 383, Society of Fermentation Technology, Japan, 1972.
17. Wang S. S., King С.-K., The Use of Coenzymes in Biochemical Reactors in Advances in Biochemical Engineering, vol. 12, Ghose T. K., Feichter A., Blakebrough N. (eds.), p. 119, Springer Verlag, New York, 1979.
18. Klibanov A. AL, Stabilization of Enzymes by Immobilization, Analyt. Biochem., 93, 1 (1979).
Опубликованы две ценные обзорные статьи, посвященные целлюлозе и «целлюлазе»:
19. Lee У. Ft., Fan L. Т., Properties and Mode of Action of Cellulase; Kinetics of Hydrolyses of Insoluble Cellulose by Cellulase, in Advances in Biochemical Engineering, vol. 17, p. 101, 131, Fietcher A., (ed.), Springer Verlag, New York, 1980.
В приведенных ниже работах подробно рассмотрена взаимосвязь между химическими реакциями и массопередачей. В некоторых из них основное внимание уделено биологическим системам, а в других — синтетическим катализаторам. Приведенный в последних работах материал, как мы уже указывали, можно после небольших изменений в терминологии и обозначениях отнести и к биологическим системам.
20. Atkinson В., Biochemical Reactors, Pion Ltd., London, 1974.
21. Weisz P. W., Diffusion and Chemical Transformation: An Interdisciplinary Excursion, Science, 179, 433 (1973).
22. Satterfield C. N., Mass Transfer in Heterogeneous Catalysis, MIT Press, Cambridge, Mass., 1970.
23. Petersen E. E., Chemical Reaction Analysis, Prentice-Hall, Inc., Englewood Cliffs, N.J., 1965.
24. Ans R., The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts, vol. 1, The Theory of the Steady State, vol. 2, Questions of Uniqueness, Stability and Transient Behavior, Clarendon Press, Oxford, 1975.
В многотомном издании под общим названием Enzyme Engineering публикуются доклады, представленные на проводящихся раз в два года конференциях по технологии ферментов, организуемых инженерным фондом. Первый том был опубликован издательством Wiley-Interscience (New York, 1972); последующие тома выпускались издательством Plenum (New York), а также публиковались в журнале Annals of the New York Academy of Sciences.