Биохимия - Химические реакции в живой клетке Том 1 - Д. Мецлер 1980

Энергетика биохимических реакций
Таблицы значений ∆G0 для биохимических соединений
«Константы», изменяющиеся с изменением pH

В уравнении (3-42), описывающем гидролиз НАТР^3- с образованием HADP^2-и Н₂РО^-, указанная стехиометрия имеет место лишь при значениях pH вблизи 6. При pH выше ~7 большая часть АТР находится в форме АТР^4- и распадается до НРО^2-₄согласно следующему уравнению:

Значение ∆G° = + 5,4 кДж∙моль^-1 для этой реакции вовсе не является тем большим отрицательным числом, каким оно должно быть для самопроизвольной реакции. Все дело здесь в том, что в числе продуктов реакции оказались ионы водорода, а стандартным состоянием для Н⁺ является не 10^-7 М, а 1 М раствор. Поэтому биохимики часто предпочитают пользоваться кажущимися константами диссоциации и кажущимися ∆G; в этом случае за стандартное состояние для ионов водорода принимается состояние, соответствующее значению pH, при котором проводится эксперимент, обычно pH 7. Получаемая таким образом pH-зависимая константа равновесия обозначается К' и определяется так:

Если в ходе реакции высвобождается один протон, как в уравнении (3-44), то будет выполняться следующее соотношение:

∆G' = ∆G° — 5,708∙pH кДж∙моль^-1 при 25 °С.       (3-46)

Вспомним, что ∆G' =—RT ln К', и еще заметим, что [Н⁺] не входит в выражение для К' [уравнение (3-45)]. При ∆С °= +5,4 кДж∙моль^-1 получаем, что в ходе гидролиза АТР при 25 °С и μ = 0,25, согласно уравнению (3-46), ∆G'(pH7) =—34,5 кДж∙моль^-1 = —8,26 ккал∙моль^-1. (3-47)

В биохимической литературе нередко используется ряд других стандартных состояний. Константа равновесия, часто обозначаемая в литературе через K_obs[наблюдаемая (observed) константа], связана с суммарной концентрацией всех ионных форм каждого из компонентов, существующих при данном pH. Так,

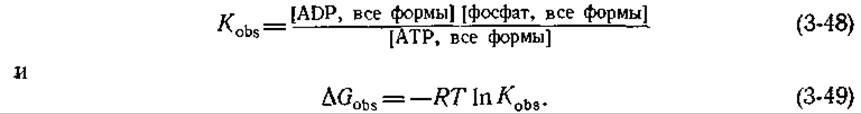
Изменение свободной энергии ∆G_obs можно связать с ∆G', исходя из соотношений между K_obsи К'. Для гидролиза АТР в интервале значений pН 2—10 K_obsесть

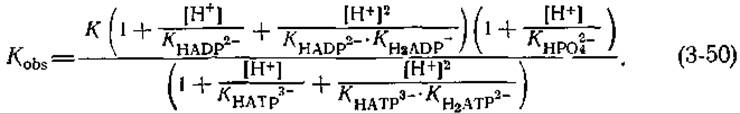
В этом уравнении K_HADP2- и т. д. — константы отдельных стадий диссоциации (табл. 3-4). Выражения в скобках — это pH-функции Михаэлиса (см. также гл. 6, разд. Д.5). Они связывают полную концентрацию данного компонента с концентрацией наиболее диссоциированной формы. Так, при pH в интервале от 2 до 10

Используя кажущиеся значения рКа (р = 0,2) для Н₂РО^-₄, HADP^2-и НАТР^3-, равные соответственно 6,78; 6,83 и 7,06 (табл. 3-4), мы получим, что при pH 7 ∆G_obs= —35,0 кДж∙моль^-1(приняв при этом, что при pH 7 ∆G' = —34,5 кДж∙моль^-1). Различие между ∆G' и ∆G_obs в этом примере невелико, но оно было бы заметно больше, если бы ионные формы, фигурирующие в уравнении (3-44), при pH 7 не являлись преобладающими.

Чтобы найти изменение свободной энергии реакции в условиях, отличных от стандартных, следует применить уравнение (3-28). Так, при pH 7 и 0,01 М активностях ADP^3-, АТР^4- и НРО^2-₄ ∆G гидролиза АТР, согласно уравнению (3-44), равно —34,5—2∙5,71=—45,9 кДж∙моль^-1 = —11,0 ккал∙моль^-1. Следовательно, для концентраций, имеющих место в клетках (как правило, это миллимоли), потенциал переноса АТР существенно выше, чем при стандартных условиях.

Чтобы найти ∆G для температуры, отличающейся от 25 °С, необходимо знать ∆H реакции. Используя уравнение (3-37), легко показать, что ∆G для температуры T₂ связано с ∆G для температуры Т₁ следующим соотношением:

Энтальпия гидролиза АТР, согласно уравнению (3-44), равна —19,7 кДж∙моль^-1. Используя это значение и применяя уравнение (3∙52), находим¹, что ∆G' (pH 7) гидролиза АТР для 38 °С равно —35,2 кДж∙моль^-1. Следует помнить, что все указанные здесь изменения свободной энергии — это кажущиеся величины, относящиеся к растворам с ионной силой ~0,25.

¹ Точное значение ∆С (pH 7) для 25 °С, использованное для получения приведенного здесь результата, равно —34,54 кДж∙моль^-1. Почти такое же значение получил автор этой книги, исходя из ∆G' = —35,19 кДж∙моль^-1 для 38 °С, приведенного в работе [11].