Биохимия - Химические реакции в живой клетке Том 1 - Д. Мецлер 1980
Как молекулы соединяются друг с другом
Количественная оценка прочности связывания
Анализ данных
При проведении биохимических исследований постоянно возникает необходимость оценить прочность связывания различных молекул друг с другом. Например, для выяснения физиологического значения таких процессов, как взаимодействие гормона с клеточной мембраной или ингибирование фермента по принципу обратной связи, могут помочь данные о том, насколько прочны связи гормона с мембраной или фермента с ингибитором. Поэтому важно понимать, каким образом можно определять прочность связывания и какие трудности при этом возникают.
Способность молекулы X связываться с молекулой Р [уравнение (4-1)] можно оценить, варьируя концентрации X и Р и определяя, как меняется при этом концентрация комплекса РХ. Прежде всего необходимо выбрать какое-то свойство, которое можно количественно охарактеризовать и по которому комплекс отличается от исходных компонентов. Например, комплекс может быть окрашен, а исходные компоненты бесцветны. Чаще всего комплекс и исходные компоненты по- разному поглощают свет определенной длины волны, иногда они имеют разные спектры кругового дихроизма или разные химические сдвиги сигналов ЯМР. Если Р — это фермент, то только распад комплекса РХ приводит к образованию продуктов реакции. Иногда скорость распада РХ (фермент-субстратного комплекса) мала по сравнению со скоростью установления равновесия между X, Р и РХ. В этом случае наблюдаемая скорость образования продукта пропорциональна концентрации комплекса.
Независимо от того, изменение какого свойства измеряется экспериментально, величина этого изменения должна возрастать по мере увеличения концентрации X при сохранении концентрации молекул Р постоянной. Обычно молярная концентрация Р в опытах бывает мала, а концентрацию X варьируют в весьма широких пределах. В этих условиях при достаточно больших значениях [X] большая часть молекул Р переходит в РХ и изменение какого-то свойства (допустим ∆А) перестает возрастать. Этот эффект, известный под названием насыщение, наблюдался в большинстве работ по исследованию процесса связывания, а также во многих физиологических процессах.
Свойство или изменение свойства, которое количественно характеризуют (∆А), при насыщении (т. е. когда все вещество Р переходит в РХ) достигает максимального значения — ∆Аmах. Отношение [РХ] к суммарной концентрации всех форм Р, присутствующих в растворе [Р]полн, называется степенью насыщения и обозначается через ![]() Если молекула Р имеет более одного центра связывания для X, то величина
Если молекула Р имеет более одного центра связывания для X, то величина ![]() характеризует долю занятых центров от общего числа центров связывания. Если обозначить через n число центров связывания в расчете на одну молекулу, то общее число центров связывания будет равно n ∙ [Р]. Величину
характеризует долю занятых центров от общего числа центров связывания. Если обозначить через n число центров связывания в расчете на одну молекулу, то общее число центров связывания будет равно n ∙ [Р]. Величину ![]() часто принимают равной ∆А/∆Аmах. Для макромолекул с несколькими центрами связывания это равенство соблюдается только при условии, что добавление каждой новой молекулы X приводит к одинаковому изменению А. Это условие выполняется не всегда, однако если оно выполняется, то должно выполняться и следующее соотношение:
часто принимают равной ∆А/∆Аmах. Для макромолекул с несколькими центрами связывания это равенство соблюдается только при условии, что добавление каждой новой молекулы X приводит к одинаковому изменению А. Это условие выполняется не всегда, однако если оно выполняется, то должно выполняться и следующее соотношение:
![]()
Индекс і обозначает число лигандов X, связанных с Р; он может меняться от 0 до n. При n = 1 степень насыщения ![]() и величину ∆А можно выразить через концентрацию несвязанного X и константу образования. Соответствующие соотношения имеют вид
и величину ∆А можно выразить через концентрацию несвязанного X и константу образования. Соответствующие соотношения имеют вид
![]()
На рис. 4-1 приведена кривая, характеризующая зависимость ![]() (или ДА) от [X] для некоторой гипотетической реакции (эту кривую иногда называют изотермой адсорбции, поскольку для получения достоверных результатов эксперименты следует проводить при постоянной температуре). Из рис. 4-1 и уравнения (4-9) можно видеть, что когда
(или ДА) от [X] для некоторой гипотетической реакции (эту кривую иногда называют изотермой адсорбции, поскольку для получения достоверных результатов эксперименты следует проводить при постоянной температуре). Из рис. 4-1 и уравнения (4-9) можно видеть, что когда
величина [X] в точности равна 1/Kf (или Кd), то ![]() Видно также, что насыщение достигается медленно, и даже в точке, соответствующей наибольшей концентрации X (8/K), степень насыщения не превышает 90%. Поскольку обычно в опытах измеряется ∆А
Видно также, что насыщение достигается медленно, и даже в точке, соответствующей наибольшей концентрации X (8/K), степень насыщения не превышает 90%. Поскольку обычно в опытах измеряется ∆А ![]() из кривой такого типа трудно определить предельное значение ∆Аmах (за исключением случаев, когда величина Kf очень велика). Однако для определения Kf необходимо знать именно ∆Аmах. В связи с этим графики, подобные представленному на рис. 4-1, используются редко, и он приведен нами здесь в основном для иллюстрации вводимых определений. Кривая, изображенная на рис. 4-1, — это равнобочная гипербола в координатах
из кривой такого типа трудно определить предельное значение ∆Аmах (за исключением случаев, когда величина Kf очень велика). Однако для определения Kf необходимо знать именно ∆Аmах. В связи с этим графики, подобные представленному на рис. 4-1, используются редко, и он приведен нами здесь в основном для иллюстрации вводимых определений. Кривая, изображенная на рис. 4-1, — это равнобочная гипербола в координатах ![]() кривые насыщения такого типа часто называют поэтому гиперболическими. Это название подчеркивает отличие изотермы адсорбции от кривых связывания несколько другого вида (разд. В.7), которые в тех же координатах носят сигмоидный (S-образный) характер.
кривые насыщения такого типа часто называют поэтому гиперболическими. Это название подчеркивает отличие изотермы адсорбции от кривых связывания несколько другого вида (разд. В.7), которые в тех же координатах носят сигмоидный (S-образный) характер.
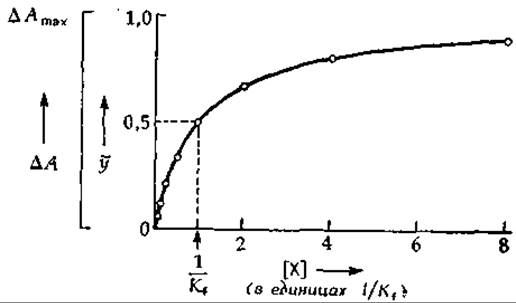
РИС. 4-1. Изотерма адсорбции—зависимость степени насыщения ![]() (или изменения какого-нибудь свойства ∆A) от концентрации вещества [X], обратимо связывающегося с макромолекулой. Кривая носит гиперболический характер;
(или изменения какого-нибудь свойства ∆A) от концентрации вещества [X], обратимо связывающегося с макромолекулой. Кривая носит гиперболический характер; ![]()
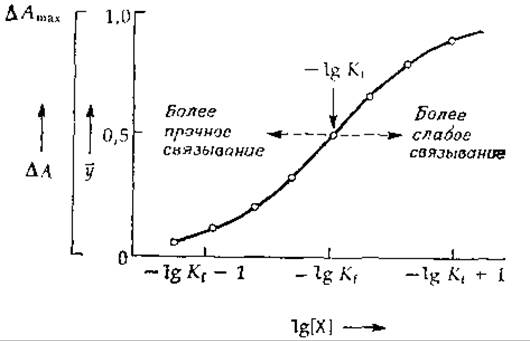
РИС 4-2. Кривая насыщения в полулогарифмическом масштабе, построенная по тем же точкам, что и кривая рис. 4-1.
Зачастую более удобно строить графики в других координатах, а именно ![]() (рис. 4-2). Перечислим причины, по которым эти координаты более удобны. 1. Кривая становится симметричной относительно средней точки, где lg[X] = —lg Kf. 2. Независимо от того, насколько велик диапазон используемых концентраций X, всегда можно выбрать масштаб, при котором все точки уместятся на одном листке бумаги. 3. Расстояния между точками на кривой, построенной в указанных координатах, приблизительно одинаковы в отличие от графика, построенного в координатах
(рис. 4-2). Перечислим причины, по которым эти координаты более удобны. 1. Кривая становится симметричной относительно средней точки, где lg[X] = —lg Kf. 2. Независимо от того, насколько велик диапазон используемых концентраций X, всегда можно выбрать масштаб, при котором все точки уместятся на одном листке бумаги. 3. Расстояния между точками на кривой, построенной в указанных координатах, приблизительно одинаковы в отличие от графика, построенного в координатах ![]() (сравните графики, приведенные на рис. 4-1 й 4-2, на которых экспериментальные точки соответствуют одним и тем же данным, причем каждое последующее значение [Х] в два раза больше предыдущего). 4. Логарифмическая шкала такого типа может быть использована для всех соединений независимо от прочности связывания, и форма кривых для всех комплексов с соотношением компонентов 1:1 одинакова. Наклон кривой
(сравните графики, приведенные на рис. 4-1 й 4-2, на которых экспериментальные точки соответствуют одним и тем же данным, причем каждое последующее значение [Х] в два раза больше предыдущего). 4. Логарифмическая шкала такого типа может быть использована для всех соединений независимо от прочности связывания, и форма кривых для всех комплексов с соотношением компонентов 1:1 одинакова. Наклон кривой ![]() в средней точке равен 0,576; изменение величины lg[X] при переходе от степени насыщения 10% к степени насыщения 90% составляет 1,81. Аналогичные кривые хорошо знакомы химикам, поскольку они напоминают по форме кривые титрования, в которых вместо —lg[X] используется pH. При переходе от более слабого комплекса к более прочному кривая смещается влево, и наоборот. Кривые такого типа очень удобно описывать математически с помощью гиперболических функций [4а].
в средней точке равен 0,576; изменение величины lg[X] при переходе от степени насыщения 10% к степени насыщения 90% составляет 1,81. Аналогичные кривые хорошо знакомы химикам, поскольку они напоминают по форме кривые титрования, в которых вместо —lg[X] используется pH. При переходе от более слабого комплекса к более прочному кривая смещается влево, и наоборот. Кривые такого типа очень удобно описывать математически с помощью гиперболических функций [4а].
Для графического представления данных по насыщению часто используют другую систему координат, известных под названием координат Скэтчарда1 (рис. 4-3). При этом по одной оси откладывают величину ∆А/[Х] ![]() в результате чего точки ложатся на прямую. Из уравнения (4-10), непосредственно вытекающего из уравнения (4-9), следует, что отрезок, отсекаемый прямой на оси абсцисс, и наклон прямой непосредственно дают значения ∆Аmах и Kt.
в результате чего точки ложатся на прямую. Из уравнения (4-10), непосредственно вытекающего из уравнения (4-9), следует, что отрезок, отсекаемый прямой на оси абсцисс, и наклон прямой непосредственно дают значения ∆Аmах и Kt.
![]()
Прежде чем приступать к получению кривых насыщения, каждому стоит прочесть прекрасную статью Деранле [5], а для того чтобы лучше понять изложенный далее материал, нужно ознакомиться с работой Дауда и Риггса [6].
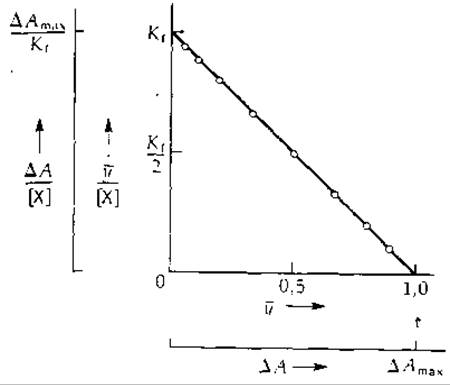
РИС. 4-3. График Скэтчарда, построенный по тем же точкам, что и кривые рис. 4-1 и 4-2. Это самый удобный линейный график для анализа данных по связыванию.
1 График Скэтчарда является наилучшим из всех линейных преобразований уравнения насыщения, и в частности графика двойных обратных координат (рис. 6-3).