Биохимия - Химические реакции в живой клетке Том 1 - Д. Мецлер 1980
Как молекулы соединяются друг с другом
Кооперативные изменения конформации
Олигомеры более высокого порядка
Математический анализ кривых связывания для олигомеров с числом субъединиц >2 более сложен, однако можно привлечь численные методы. Пользуясь уравнениями, приведенными в литературе для описания той или иной системы, необходимо соблюдать осторожность и быть уверенным, что они действительно применимы к данной ситуации. Рассмотрим две тетрамерные структуры:
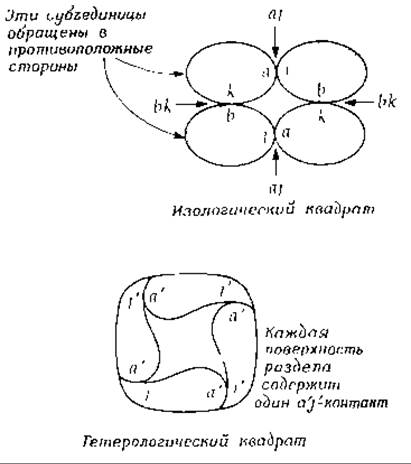
Свободная энергия образования изологичеcкого квадрата (изображенного также на рис. 4-9, Б) определяется энергией aj- и bk-взаимодействий.
Таким образом, согласно Корниш-Боудену и Кошланду [62], для тетрамера в целом справедливы следующие соотношения:

Поскольку величины свободных энергий аддитивны, константа образования тетрамера будет равна произведению констант образования, соответствующих отдельным взаимодействиям; так, KajAА представляет собой константу образования димера, в котором имеется лишь одна связь aj.
В изологическом тетраэдре (рис. 4-9, В) должен учитываться третий набор парных взаимодействий — cl. (Однако третья константа взаимодействия в отличие от констант типа КajАА и КbkAA представляет собой безразмерную величину). Гетерологический же квадрат характеризуется лишь одной константой взаимодействия.
Рассмотрим теперь присоединение одной молекулы X к изологическому тетрамеру, сопровождающееся конформационным переходом в одной субъединице:
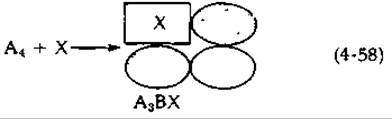
При этом несколько изменяется одно аj-взаимодействие и одно bk. Константа равновесия для связывания X с тетрамером будет определяться следующим уравнением:
![]()
Появление в уравнении статистического множителя 4 обусловлено тем, что комплекс А3ВХ можно образовать четырьмя опособами. При присоединении второй молекулы X возможно такое геометрическое расположение субъединиц:
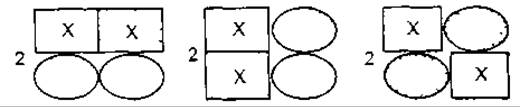
Каждая из форм может образоваться двумя опособами. Нетрудно записать микроскопические константы для связывания второй молекулы X как сумму трех членов. Ясно, что три варианта связывания второй молекулы X не равновероятны, поскольку константы, соответствующие взаимодействиям aj и bk, различаются. Таким образом, олигомер будет связываться с лигандом X преимущественно каким-то одним способом.
Гетерологический тетрамер A2B2X2 может быть представлен двумя геометрическими формами. И опять различные варианты упаковки не равновероятны. Вероятность их реализации зависит от конкретных значений констант взаимодействия1.
Все изложенное выше может показаться просто длинным и не слишком нужным упражнением, однако оно закладывает основы, которые необходимы для решения конкретных задач. Следует, однако, помнить, что для применения математических моделей необходимо вводить некоторые упрощения. Реальные белки могут существовать более чем в двух стабильных конформациях [11], а на их наружной поверхности имеется множество участков, потенциально способных связывать самые разные молекулы — как крупные, так и мелкие. Заполнение практически любого из этих участков может влиять на функциональные свойства белка.
1 Заметим, что в гетерологическом тетрамере А4 имеет место лишь один тип взаимодействия между субъединицами. Однако, как только происходит присоединение одной молекулы X и одна субъединица переходит в конформацию В, сразу появляются два варнаита аj-взаимодействий. (В первом из них группа а находится в конформере А, а во втором — в конформере В). Поскольку число этих типов взаимодействий одинаково, их можно рассматривать вместе.