БИОХИМИЯ - Л. Страйер - 1984

ТОМ 1

ЧАСТЬ I. КОНФОРМАЦИЯ И ДИНАМИКА

ГЛАВА 6. ВВЕДЕНИЕ В ЭНЗИМОЛОГИЮ

6.9. Кинетика многих ферментов описывается моделью Михаэлиса - Ментен

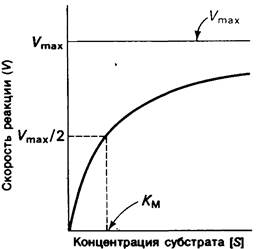
Для многих ферментов скорость катализа К, таким образом, зависит от концентрации субстрата [S], как это показано на рис. 6.12. При постоянной концентрации фермента и малых значениях [S] V почти прямо пропорциональна [S]. При высоких значениях [S] V почти не зависит от [S]. В 1913 г. Леонор Михаэлис и Мод Ментен (L. Michaelis, М. Menten) предложили простую модель, объясняющую такую кинетику. Основная их посылка состояла в том, что образование специфического фермент-субстратного комплекса является необходимым промежуточным этапом катализа. Предложенная ими модель, которая простейшим образом описывает кинетические свойства многих ферментов, состоит в следующем:

(1)

Рис. 6.12. График зависимости скорости реакции V от концентрации субстрата [S] для фермента, подчиняющегося кинетике Михаэлиса - Ментен (V_mах- максимальная скорость, К_м- константа Михаэлиса)

Фермент Е соединяется с субстратом S, образуя ЕS-комплекс; константа скорости этого процесса - k₁. Судьба ЕS-комплекса складывается двояко: он может либо диссоциировать на Е и S с константой скорости к₂, либо подвергаться дальнейшему превращению, образуя продукт Р, с константой скорости к₃. Постулируется, что продукт реакции Р не превращается в исходный субстрат S; это условие соблюдается на начальной стадии реакции, пока концентрация продукта не достигает ощутимого количества.

Как связана скорость катализа с концентрацией субстрата и фермента и скоростями отдельных этапов реакции? Начнем с того, что скорость ферментативной реакции равна произведению концентрации комплекса ЕS на константу к₃:

V = к₃ [ЕS]. (2)

Выразим [ЕS] через известные величины. Скорости образования и распада ЕS составляют:

Скорость образования ЕS =k₁ [Е] [S]. (3)

Скорость распада ЕS = (к₂ + к₃) [ЕS]. (4)

Определим скорость катализа в стационарных условиях. Стационарные условия характеризуются тем, что концентрация промежуточных продуктов остается постоянной, тогда как концентрации исходных и конечных продуктов меняются. Это имеет место в том случае, когда скорость синтеза ЕS-комплекса оказывается равной скорости его распада. Если левые части равенств (3) и (4) равны между собой, то равны и правые, т. е.

k₁ [Е] [S] = (к₂ + к₃) [ЕS]. (5)

Преобразуем это уравнение:

(6)

Уравнение (6) можно упростить, если ввести новую константу К_м, называемую константой Михаэлиса:

(7)

Введем К_м в уравнение (6):

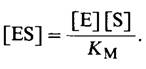(8)

Рассмотрим числитель в последнем выражении. Концентрация несвязанного субстрата [S] практически равна общей концентрации субстрата при условии, что концентрация фермента значительно ниже концентрации субстрата. Концентрация несвязанного фермента (Е) равна общей концентрации фермента Е_т минус концентрация комплекса ЕS:

[Е]=[Е_Т]-[ЕS]. (9)

Подставим это выражение в уравнение (8):

[ЕS] = ([Ет] — [ЕS]) [S]/K_М (10)

Решение уравнения (10) относительно [ЕS] дает

(11)

или

(12)

Подставим выражение (12) в уравнение (2):

(13)

Максимальная скорость реакции Vm_ах достигается при насыщении активных центров фермента субстратом, т.е, когда [S] намного выше К_м; при этом условии [S]/([S] + К_м) приближается к единице. Следовательно,

V_max = kз [Ет]. (14)

Подставив это выражение в выражение (13), мы получим уравнение Михаэлиса-Ментен:

(15)

Это уравнение соответствует кинетическим данным, представленным на рис. 6.12. При низких концентрациях субстрата, когда [S] намного ниже K_м, V = [S] V_max/К_м, т.е. скорость прямо пропорциональна концентрации субстрата. При высоких концентрациях субстрата, когда [S] намного выше, чем К_м, V = V_max, т. е. скорость реакции максимальна и не зависит от концентрации субстрата.

Значение К_м выступает с очевидностью из уравнения (15). Если [s] = Км, то V = V_max/2. Таким образом, К_м равна концентрации субстрата, при которой скорость реакции составляет половину максимальной.