Молекулярная биология: Структура и функции белков - Степанов В.М. 2005

Ферменты
Основные положения кинетики ферментативного катализа

Основы кинетики ферментативных реакций были заложены Л. Михаэлисом и М. Ментен еще в 1913 г. Предложенное ими уравнение, связывающее скорость реакции с концентрациями фермента и субстрата, в дальнейшем преобразовывалось, однако подход в принципиальных чертах сохранился и за уравнением остались эти имена.

Согласно модели Михаэлиса-Ментен, фермент Е и субстрат S взаимодействуют со скоростью, харакгеризуемой константой k_+1, образуя фермент-субстратный комплекс ES, получивший название комплекс Михаэлиса. Этот комплекс, в котором субстрат, присоединенный к ферменту нековалентными связями, еще сохраняет свою химическую природу, распадается с константой скорости k_-1, на фермент и субстрат, но может и превратиться в продукт (или продукты) Р, высвободив фермент Е, со скоростью, характеризуемой константой k₊₂.

Как правило, фермент-субстратный комплекс ES чаще распадается на исходные компоненты, чем превращается с образованием продукта реакции Р, т.е k₊₁ ≫ k₊₂. Конечно, именно превращение субстрата в продукт представляет главный интерес при изучении ферментативных реакций. Накоплением продукта в единицу времени и определяется скорость реакции.

При выводе уравнения Михаэлнса-Ментен необходимо прежде всего найти зависимость концентрации фермент-субстратного комплекса от концентраций фермента и субстрата, поскольку скорость образования продукта пропорциональна концентрации комплекса ES. Скорость образования ES равна k₊₁ [Е] [S]. Скорость же его распада определяется суммой двух процессов: диссоциации фермент-субстратного комплекса на компоненты со скоростью k_-1[ES] и его распада с образованием продукта со скоростью k₊₂[ES],

Итак, скорость распада комплекса ES по двум путям равна сумме этих скоростей (k_-1 + k₊₂)[ES]. Кинетика Михаэлиса—Ментен приложима к уже установившимся, стационарным процессам, когда скорости образования и распада комплекса Михаэлиса равны, т.е, сохраняется его постоянная концентрация. Для такого процесса справедливо равенство

преобразуя которое получим

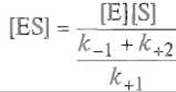
Дробь

называют константой Михаэлиса Кm. Легко видеть, что она характеризует соотношение скоростей распада (числитель) и образования (знаменатель) комплекса Михаэлиса ES. Если k₊₂ мала по сравнению с k_-1, т.е. распад комплекса на исходные компоненты — фермент и субстрат — оказывается значительно вероятнее, чем его распад с образованием продукта Р, величиной k₊₂ можно пренебречь и константа Михаэлиса оказывается равной константе диссоциации субстрата

Как уже отмечалось, это соотношение часто оказывается справедливым, поэтому константу Михаэлиса К_m нередко приравнивают КS. Следует, однако, помнить об условности такого упрощения. Заменяя дробь в знаменателе предыдущего уравнения на К_m, получаем

Заметим, что в приведенное уравнение входят текущие концентрации свободного фермента и субстрата, которые, строго говоря, не совпадают с их начальными концентрациями, гораздо легче поддающимися определению. Впрочем, различиями в начальной [S_T] и текущей концентрациях субстрата можно пренебречь, приняв [S_T] ≈ [S], поскольку уравнение Михаэлиса-Ментен справедливо только для небольших степеней превращения субстрата (о чем нельзя забывать, определяя активность ферментов). Напротив, текущая концентрация фермента существенно отличается от его полной концентрации [Е_T] вследствие связывания большей или меньшей доли молекул фермента в комплекс Михаэлиса:

Подставляя это выражение для текущей концентрации фермента в приведенное выше уравнение, после преобразований получаем

Это уравнение описывает зависимость концентрации фермент-субстратного комплекса от исходных концентраций фермента и субстрата. Так как скорость образования продукта реакции V равна k₊₂[ES], то

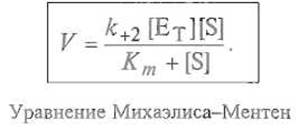
Следует иметь в виду, что это уравнение определяет начальную скорость стационарной реакции V₀, индекс «0» опущен для упрощения. Из выведенного уравнения следует, что скорость реакции пропорциональна общей концентрации фермента, тогда как ее зависимость концентрации субстрата оказывается значительно более сложной.

Рассмотрим, как выглядит эта зависимость в наиболее характерных случаях. Напомним, что

и если k₊₂≪ k_-1 (что наблюдается достаточно часто), то в первом приближении К_m≈ K_S, иначе говоря, константа Михаэлиса равна константе диссоциации фермент-субстратного комплекса — «субстратной константе».

1. Если концентрация субстрата много меньше Кm, т.е. [S] ≪ К_m (случай, соответствующий действительно низкой концентрации субстрата или плохому его связыванию ферментом — большому значению К_m), то величиной [S] в знаменателе уравнения Михаэлиса-Ментен можно пренебречь и скорость реакции оказывается пропорциональной концентрации и субстрата и фермента, а само уравнение приобретает вид

Это выражение соответствует уравнению скорости бимолекулярной реакции. Дробь которая отвечает константе скорости бимолекулярной реакции, иногда называют бимолекулярной константой скорости и используют соответствующие величины при сопоставлении эффективности действия однотипных ферментов

2. Если концентрация субстрата много больше К_m, [S] ≫ К_m (концентрация субстрата сама по себе велика или фермент хорошо связывает субстрат, чему соответствует низкая К_m), то величиной К_m в знаменателе можно пренебречь и скорость реакции V = k₊₂[Е_T] оказывается пропорциональной концентрации фермента, а от концентрации субстрата не зависит. Иными словами, фермент оказывается насыщенным субстратом, свободного фермента в реакционной смеси нет. Стоит обратить внимание на то, что концентрация субстрата в ферментативных реакциях важна не сама по себе, а в сопоставлении с константой Михаэлиса, характеризующей соответствие данного субстрата ферменту.

Сказанное иллюстрирует рис. 10.1. При небольших концентрациях субстрата скорость реакции пропорциональна его содержанию в реакционной смеси, затем наблюдается все возрастающее отклонение зависимости от линейной и, наконец, при концентрациях субстрата, значительно превышающих К_m, зависимость скорости реакции от концентрации субстрата практически исчезает, причем сама скорость достигает максимального (при данной концентрации фермента) значения:

V_max = k₊₂[E_T]

Следовательно,

Это другая форма уравнения Михаэлиса-Ментен.

3. Если концентрация субстрата равна константе Михаэлиса, то К_m+ [S] =2[S] и V= V_max/2.

Приведенное соотношение показывает физический смысл константы Михаэлиса для пары фермент-субстрат: она численно равна концентрации субстрата, при которой скорость реакции достигает половины максимальной величины.

Необходимо иметь в виду, что кинетика Михаэлиса—Ментен справедлива для многих, но не для всех реакций, катализируемых ферментами. Существенные отклонения от нее обнаруживают, в частности, ферменты, активность которых возрастает с увеличением концентрации субстрата.

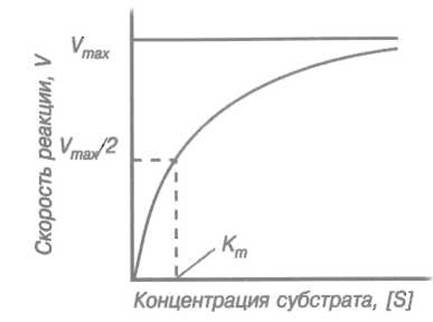
Рис. 10.1. Зависимость скорости V катализируемой ферментом реакции от концентрации субстрата

Величины V_max и К_m очень важны для характеристики ферментных реакций; разработан ряд приемов их определения. Наиболее популярен способ расчета данных в соответствии с преобразованным уравнением Михаэлиса—Ментен, так называемый метод двойных обратных величин, предложенный Г. Лайнуивером и Д. Берком. Уравнение Михаэлиса-Ментен преобразуют так, чтобы оно выражало величину, обратную скорости реакции 1/V (т.е. время, необходимое для превращения определенного количества субстрата) в функции обратной концентрации субстрата (его разбавления) 1/S:

В такой форме уравнение Михаэлиса-Ментен эквивалентно уравнению прямой вида у = ах + b, где у = 1/V, х = 1/S,

т.е. описывает прямую, отсекающую отрезки на координатных осях (рис. 10.2). Если при возрастании концентрации субстрата до очень высоких значений 1/[S] стремится к нулю, то 1/V оказывается равным 1/V_mах. Таким образом, измерив отрезок, отсекаемый прямой на оси 1/V, можно вычислить V_max. Если же 1/V= 0, то

и К_m оказывается равной — [S].

Известны и другие, в том числе и более удобные для обработки данных, преобразования уравнения Михаэлиса-Ментен, использование которых описано в специальных руководствах. В последнее время расчеты на ЭВМ вытесняют графические методы.

Применение уравнения Михаэлиса—Ментен позволяет количественно характеризовать эффективность действия ферментов, сравнивать их действие на различные субстраты. Как уже —1/К_m — отрезок, отсекаемый на оси х, 1/V_mах — отрезок, отсекаемый на оси у говорилось, значение Кm с определенными оговорками позволяет оценить сродство различных ферментов к их субстратам. Величины Кm лежат в весьма широком интервале концентраций, обычно начинаясь с миллимолярных. Встречаются и значительно большие значения Кm, что может быть связано с использованием субстратов, не вполне отвечающих специфичности фермента. Понятно, что для небольших субстратов, например НСО₃, нелегко организовать достаточно развитую систему взаимодействия с ферментом, поэтому величины Кm, вероятно, будут высокими.

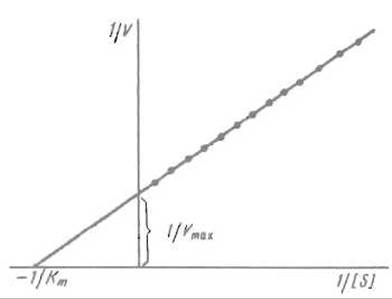
Рис. 10.2. Зависимость величины, обратной скорости реакции 1/V (время, затрачиваемое на превращение единицы вещества), от величины, обратной концентрации субстрата 1/[S] (разведение).

Константы Михаэлиса становятся значительно ниже, а связывание эффективнее для протяженного субстрата, и с ним возможно установление большого числа нековалентных контактов. Так, панкреатическая эластаза (фермент, природными субстратами которого являются белки или пептиды) весьма слабо связывает простейший модельный субстрат — метиловый эфир ацетил-L-аланина. В этом случае К_m составляет 170 мМ. С удлинением пептидной цепи Кm быстро понижается, связывание улучшается. Так, для метилового эфира ацетил-аланил-аланина Кm равна 22 мМ, для метилового эфира ацетил-аланил-аланил-аланина — 0,4 мМ.

Впрочем, не следует думать, что в процессе эволюции ферментов действуют факторы, направленные на постоянное понижение Кm и улучшение связывания субстратов. По-видимому, достигается оптимальное связывание, характерное для каждой пары фермент-субстрат. В клетке субстраты многих ферментов содержатся в концентрациях, существенно меньших К_m, а следовательно, ферменты не работают в режиме насыщения. Таким образом, для природных систем типична ситуация, когда скорость ферментативной реакции зависит от концентрации субстрата и повышение последней не требует непременно усиления биосинтеза фермента.

А. Фершт и сотрудники, изучая свойства тирозил-РНК-синтетазы, обратили внимание на то, что К_m для одного из субстратов — АТФ — равна 2,5 мМ, что на несколько порядков выше констант диссоциации, известных для комплексов АТФ с другими белками. Так, Кm миозина по АТФ равна 10^-10 мМ. Совершенно очевидно, что прочное связывание такой крупной молекулы, как аденозин-трифосфат, способной образовывать целую сеть нековалентных связей с белком, вполне осуществимо. Эта возможность не реализована в тирозил-тРНК-синтетазе не потому, что фермент несовершенен. Видимо, прочное связывание АТФ с участием большого числа фермент-субстратных контактов привело бы к жесткой системе, в которой перемещения субстрата относительно каталитического центра были бы крайне затруднены, что снизило бы эффективность катализа. К тому же такое «совершенство» излишне, поскольку внутриклеточная концентрация АТФ близка к 2-3 мМ, а значит, «идеальный» фермент с лучшим связыванием вряд ли получил бы серьезный выигрыш за счет снижения К_m.

Важной характеристикой эффективности действия фермента является константа k₊₂, описывающая распад фермент-субстратного комплекса с образованием продукта реакции. Как было показано выше, V_mах = k₊₂ [Е_T] Зная общую концентрацию [Е_T] (для этого необходимо не просто знать концентрацию белка в растворе, а определить, пользуясь специально разработанными методами, концентрацию активных центров), можно рассчитать число молекул субстрата, превращающихся в продукт за единицу времени (1 с) при полном насыщении фермента субстратом. Эта величина, которую называют число оборотов, весьма различна у разных ферментов. Так, для карбангидразы она равна 60 000, для лизоцима — всего лишь 0,5. Следует подчеркнуть, что число оборотов характеризует максимально возможную скорость работы фермента, но не его эффективность в реальных условиях, когда насыщения субстратом нет.

Если механизм превращения ES в продукт более сложен, в частности многостадиен, константу k₊₁ заменяют константой реакции первого порядка k_кат.

Более точную меру эффективности в условиях, приближающихся к реальным, дает бимолекулярная константа скорости k₊₂/К_m. Подставляя в это выражение К_m = (k_-1 + k₊₂)/k₊₁, получим

Анализируя это выражение, можно видеть, что его величина существенно зависит от величины k₊₁, т.е. от скорости образования комплекса Михаэлиса, а последняя имеет свой предел, определяемый скоростью диффузии частиц в растворе, и не может превышать число столкновений субстрата и фермента. Действительно, известны ферменты, например карбангидраза и ацетилхолинэстераза, для которых величина k_кат/К_m близка к пределу и ограничивается только частотой столкновений фермента и субстрата.