Химия белка - Часть 1 - Общая химия белка - Ашмарин И. П 1968
Электрохимия белков. Взаимодействие белков с водой
Электрофорез белков в жидкой среде. Метод подвижной границы
Электрофоретическое разделение белков в водной среде основано на способности их заряженных частиц перемещаться относительно растворителя под влиянием внешнего электрического поля. Если концентрация водородных ионов в растворителе не равна изоэлектрической точке, то скорость перемещения частиц зависит от величины их свободного заряда, размера и формы. Поскольку даже близкородственные белки, например, некоторые фракции сывороточного альбумина, имеют весьма различную электрофоретическую подвижность и поскольку их подвижность изменяется неодинаково при изменениях pH и состава буферных растворов, электрофорез может быть с успехом применен для разделения белковых смесей и характеристики отдельных белков.
Хотя метод электрофореза известен уже со второй половины XIX в., точные измерения на чистых белках стали проводить лишь после создания Тизелиусом усовершенствованного аппарата для электрофоретического анализа методом подвижной границы. В этом приборе электрофоретическая кювета помещалась в низкотемпературный термостат, благодаря чему для разделения белков можно было использовать высокие градиенты потенциала, избежав тепловой конвекции. Сама кювета имела прямоугольное сечение, оптические поверхности и смещающиеся относительно друг друга части. Это позволило получать четкие границы раздела между белковым и буферным растворами и наблюдать изменения показателя преломления в зоне подвижных границ с помощью теневой оптической системы, использующей принцип Фуко—Теплера.
Электрофорез белков в жидкой среде имеет как преимущества, так и недостатки по сравнению с электрофорезом на нейтральных носителях. Этот метод незаменим для количественных определений электрофоретической подвижности и изоэлектрической точки белков, для оценки радиуса их молекулы и полноты очистки белка. Он широко применяется также для изучения процессов расщепления белков ферментами и их взаимодействия с различными ионами. Преимуществом метода является также и то, что границы раздела и процесс выявления отдельных фракций можно непосредственно наблюдать в течение всего опыта. Недостатками же метода являются невозможность выделения отдельных фракций из кюветы, загрязнение промежуточных фракций примесями соседних и, наконец, дороговизна и сложность аппаратуры. Таким образом, метод подвижной границы является аналитическим методом.
Прежде чем перейти к изложению некоторых принципов электрофореза белков в жидкой среде, необходимо вкратце остановиться па конструкции электрофоретической кюветы, а также на регистрации изменения показателя преломления с помощью теневой оптической системы.
Кювета Тизелиуса представляет собой U-образную трубку с прямоугольным поперечным сечением, разделенную на три части, смещающиеся одна относительно другой. Благодаря этому удается создать четкие границы раздела между белковым и буферным растворами в верхней части левого колена и в нижней правого, которые и регистрируются с помощью соответствующей оптической системы.
Напомним, что при переходе света из одной среды в другую с иным коэффициентом преломления направление луча меняется. Это изменение направления луча происходит резко тогда, когда показатель преломления на границе раздела меняется скачкообразно, как, например, в случае двух несмешивающихся жидкостей. Если же луч проходит размытую границу раздела между двумя смешивающимися жидкостями (белковый и буферный растворы), то коэффициент преломления меняются постепенно. При этом происходит постепенное преломление луча, т. е. его искривление. Это постепенное изменение коэффициента преломления носит название градиента показателя преломления, или градиента рефракции. Практически важно то, что искривление луча вследствие градиента рефракции вызывает его большее отклонение, нежели простое преломление.
Градиент показателя преломления пропорционален градиенту концентрации (dc/dx) и достигает максимальной величины в середине зоны раздела между белковым и буферным растворами, т. е. в том месте, где должна пройти идеальная граница раздела. В обе стороны от этой границы величина градиента рефракции убывает; очевидно, что его кривая имеет вид пика.
Выявление и запись кривой градиента рефракции осуществляется с помощью теневых оптических систем, использующих принцип Фуко—Теплера. Одна из таких систем — с наклонной щелью и цилиндрической линзой — представлена на рис. 45. Эта оптическая система носит названия системы скрещенных диафрагм, системы Фильпот—Свенсена, «шлирен»-системы и широко применяется для регистрации границ раздела белковый раствор — растворитель не только при электрофорезе, но и при ультрацентрифугировании.
Раствор в вертикальной U-образной кювете 1 освещается горизонтальным пучком света. Пучок света проходит через раствор и затем через наклонную щель 2 второго экрана, цилиндрическую линзу 3 с вертикально расположенной осью и попадает на матовый экран 4 фотокамеры. Цилиндрическая линза фокусирует пучок света на матовом экране; при этом она не изменяет вертикальной координаты Н точки в изображении кюветы, но в сочетании с наклонной щелью может смещать ее вдоль поперечной оси N. Если в растворе, находящемся в кювете, нет никакой границы раздела (слой h0), то узкий пучок света, проходящий через наклонную щель в точке У0, не отклоняется по горизонтали и даст на экране узкую вертикальную полоску света N0, которая дает основную линию. При наличии границы раздела в кювете свет, проходящий через слой hm с максимальным градиентом рефракции, отклоняется вниз до Уm, пройдя через наклонную щель, смещается цилиндрической линзой влево по горизонтали, образуя пик Nm. Лучи, прошедшие через кювету в слоях hn, с меньшим показателем преломления, соответственно отклонятся вниз до Уn и дадут боковые стороны пика. В результате на экране будет видна вся кривая градиента показателя преломления.
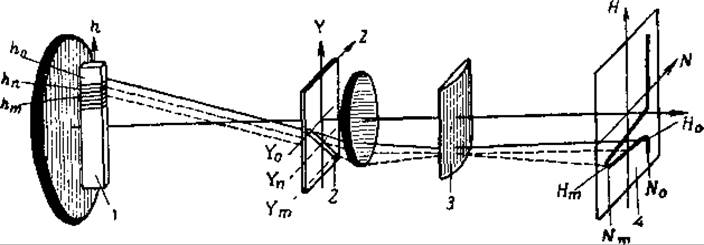
Рис. 45. Схема оптической системы с наклонной щелью и цилиндрической линзой (из Нейрата и Бэйли, 1956). Пояснения в тексте
При электрофорезе благодаря движению белковой смеси и ее разделению на отдельные компоненты произойдет не только перемещение границы раздела белковый раствор—растворитель, но и образование новых зон раздела между отдельными фракциями белков. Соответственно эти зоны раздела будут изображены на матовом экране в виде новых пиков градиентов показателей преломления. Таким образом, в методе подвижной границы происходит регистрация не самих белковых фракций, а зон раздела между ними и между крайними белковыми фракциями и растворителем, причем число пиков градиентов рефракции точно соответствует числу фракций белков. Пример такой кривой градиентов показателей преломления для белков сыворотки крови представлен на рис. 46.
Поскольку перед разделением белковая смесь находится только в нижней и средней секциях одного отделения кюветы, то при электрофорезе происходит нисходящее перемещение границы раздела белок—растворитель в одном и восходящее перемещение в другом колене кюветы.
В результате получают две диаграммы, которые вертикально симметричны и соответствуют нисходящей и восходящей границам. Обычно производят снимки только нисходящей границы.
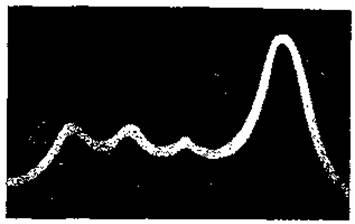
Рис. 46. Электрофоретическая диаграмма белков сыворотки крови (из Гауровица, 1965).
Перейдем к рассмотрению электрофоретической подвижности, т. е. скорости перемещения частицы при напряженности электрического поля, равной единице. Вначале рассмотрим перемещение шарообразной белковой молекулы в воде. Под действием электрического поля частицы будут двигаться со все возрастающей скоростью, пока вязкостное сопротивление среды и электрическая сила не станут равны друг другу. Частица приобретает постоянную скорость перемещения, которая, согласно закону Стокса, равна:
![]()
где Q — свободный заряд частицы, Е — напряженность электрического поля и к — радиус частицы.
Определить радиус гидратированной частицы весьма трудно. Однако этот параметр можно исключить, введя понятия потенциала на поверхности шаровой частицы (электрокинетический потенциал, дзета-потенциал). Дзета-потенциал соответствует полной разности потенциалов между поверхностью частицы и глубиной раствора и может быть определен из следующего уравнения:
![]()
где ε — диэлектрическая постоянная среды. Подставляя значение к в уравнение (58), можно определить значение величины электрофоретической подвижности:
![]()
Однако молекула белка движется не в воде, а в электролите, ионы которого оказывают определенное влияние на движение частицы. Заряженная молекула притягивает ионы противоположного знака, которые образуют вокруг нее сферическую оболочку, имеющую равный по величине заряд. Поскольку такая оболочка стремится двигаться в направлении, обратном направлению движения белковой молекулы, то скорость движения последней в электрическом поле уменьшается. Толщина такой сферической оболочки, согласно теории Дебая и Хюккеля, равна:
![]()
где μ — ионная сила. Очевидно, что толщина оболочки обратно пропорциональна ионной силе буферного раствора. В результате наличия ионной оболочки ζ-потенциал иона белка уменьшится на величину, равную ее поверхностному потенциалу. Поскольку радиус полого шара равен r+1/x, то потенциал на его поверхности составляет Qλ/ε∙(1+rx). Следовательно, ζ-потенциал белкового иона будет равен:
![]()
Подставив значение ζ в уравнение (60), можно определить подвижность частиц белка в электролите. Очевидно, что подвижность белка в результате снижения ζ-потенциала его частицы уменьшается. Поскольку вышеприведенные уравнения справедливы только для малых шарообразных молекул, то для белковых частиц в формулу С-потенциала и подвижности вносят поправку f(rх), величина которой варьирует от 1 до 1,5:
![]()
Однако величины заряда и радиуса молекулы не могут быть получены непосредственно из опыта, так же как и величина ζ-потенциала. Все эти характеристики белковой молекулы могут быть лишь рассчитаны на основании величины электрофоретической подвижности, непосредственно определяемой в эксперименте. Подвижность заряженной частицы можно выразить при помощи следующей формулы:
![]()
Скорость определяют, изменив то расстояние dx, которое пройдет граница раздела между белком и буфером за единицу времени; напряженность поля рассчитывают по закону Ома:
![]()
где J — сила тока в а, А — поперечное сечение кюветы в см2 и σр — удельная электропроводность белкового раствора, которая определяется экспериментально и равна
![]()
Здесь С — постоянная сосуда и Rp — сопротивление белкового раствора. Отсюда
![]()
Подставляя эти значения в уравнение (64), получим
![]()
Все эти величины могут быть измерены непосредственно в опыте. Подвижность имеет тот же знак, что и свободный заряд белковой молекулы; т. е., если белковая граница перемещается к катоду, то подвижность будет положительная, а если граница двигается к аноду, то — отрицательная. Таким образом, определение подвижности белковой молекулы позволяет, пользуясь формулами (60) — (64), рассчитать не только ее заряд, но и радиус, а также ζ-потенциал. Вместе с тем измерения подвижности при различных значениях pH позволяют нам определить изоэлектрическую точку белка. Напомним, что изоэлектрической точкой белка называется то значение pH, при котором подвижность равна нулю и белковая молекула имеет равное число положительных и отрицательных зарядов.
В заключение необходимо отметить, что метод подвижной границы позволяет определить и соотношение отдельных белковых фракций в их смеси. Поскольку площадь пика градиента рефракции пропорциональна концентрации белка, то, приняв сумму площадей всех пиков за 100, мы можем легко высчитать процентное соотношение отдельных фракций.